 |
B.3. Линейные оптимизационные задачи
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА №1.
Решение задач линейного программирования
Цель работы: Изучение возможностей пакета MS Excel при решении задач линейного программирования. Приобретение навыков решения задач линейного программирования.
Краткие теоретические сведения.
B.1. Основные понятия и положения
Показатель, по величине которого оценивают, является ли решение оптимальным, называется критерием оптимальности. В качестве критерия оптимальности наиболее часто принимается экономический критерий, представляющий собой минимум затрат (финансовых, сырьевых, энергетических, трудовых) на реализацию поставленной задачи. При заданной или ограниченной величине указанных затрат экономический критерий выражается в получении максимальной прибыли.
В электроэнергетике в зависимости от требований поставленной задачи могут приниматься и другие критерии оптимальности, в частности:
критерий надежности электроснабжения;
критерий качества электроэнергии;
критерий наименьшего отрицательного воздействия на окружающую среду (экологический критерий).
Решение оптимизационной задачи включает в себя следующие этапы:
1. Сбор исходной информации (исходных данных).
2. Составление математической модели, под которой понимается формализованное математическое описание решаемой задачи.
3. Выбор метода решения, определяемого видом математической модели.
4. Выполнение математических вычислений, поручаемое, как правило, компьютеру.
5. Анализ решения задачи.
B.2. Математическая модель
Формализованное математическое описание оптимизационной задачи, другими словами, математическая модель включает в себя:
|
|
|
целевую функцию;
ограничения;
граничные условия.
Целевая функция представляет собой математическую запись критерия оптимальности. При решении оптимизационной задачи ищется экстремум целевой функции, например минимальные затраты или максимальная прибыль. Обобщенная запись целевой функции имеет следующий вид:
Z(х 1, х2,... хn) → extr, (1.1)
где х 1, х2,... хn – искомые переменные, значения которых вычисляются в процессе решения задачи; общее количество переменных равно n.
Искомые переменные по своему характеру делятся на непрерывные, дискретные и целочисленные. Если переменная может принимать любые значения, такая переменная называется непрерывной. Примером непрерывной переменной может служить мощность, передаваемая по линии электропередачи.
Если переменная может принимать только значения целых чисел, такая переменная называется целочисленной. Примером целочисленной переменной может служить количество трансформаторов для электроснабжения объекта или количество изделий, выпускаемых промышленным предприятием.
Если переменная может принимать только определенные значения, такая переменная называется дискретной. Примером дискретной переменной может служить искомая мощность трансформатора или искомое сечение линии электропередачи. Значения таких величин регламентируются ГОСТами. Например, мощности трансформаторов составляют ряд … 630, 1000, 1600, … кВА, а сечения линии электропередачи – ряд … 50, 70, 95 … мм2. Распространенной задачей с дискретными переменными является задача выбора варианта из числа заданных.
Зависимость между переменными в целевой функции (1.1) может быть линейной или нелинейной. Напомним, что линейной называется такая зависимость, в которую переменные xi (i =1, 2, 3, … n) входят только в первой степени и с этими переменными выполняются только действия сложения, вычитания и умножения на постоянный коэффициент. Во всех других случаях зависимость будет нелинейной.
|
|
|
Нелинейная целевая функция в заданном диапазоне изменения переменных может иметь один экстремум или несколько экстремумов. В первом случае функция будет одноэкстремальной, во втором – многоэкстремальной. На рис. 1.1 приведены примеры одноэкстремальной (один минимум) и многоэкстремальной (два минимума и один максимум) функции Z(x) одной переменной в диапазоне изменения этой переменной d < x < D.
Рисунок В.1. Одноэкстремальная (а) и многоэкстремальная (б) функции
В случае многоэкстремальной функции каждый экстремум называется локальным. У многоэкстремальных функций ищется глобальный экстремум (наименьший минимум или наибольший максимум). Так при отыскании минимума функции, приведенной на рис. 1.1,б ищется глобальный минимум, отвечающий точке 3.
Ограничения представляют собой различные технические, экономические, экологические условия, учитываемые при решении задачи. Ограничения представляют собой зависимости между переменными х 1, х2,... хn, задаваемые в форме неравенств или равенств
f1(х 1, х2,... хn) < b 1;
f2(х 1, х2,... хn) = b 2;
...................
fm(х 1, х2,... хn) > bm.
Общее количество ограничений равно m. Правые части ограничений, представляющие собой постоянные коэффициенты bj (j =1, 2, … m), называются свободными членами.
Как и в выражении целевой функции (1.1), зависимости между переменными в системе ограничений (1.2) могут быть линейными и нелинейными.
Граничные условия устанавливают диапазон изменения искомых переменных
di < х i < Di, i= 1, 2, … n, (1.3)
где di и Di - соответственно нижняя и верхняя границы диапазона изменения переменной xi.
Наиболее часто в технических задачах все искомые переменные, как правило, неотрицательны. В этом случае граничные условия имеют следующий вид:
xi ≥0, где i =1 ,2, … n.
При наличии ограничений и граничных условий ищется уже не абсолютный, а относительный экстремум целевой функции. На рис. 1.2 показана некоторая функция одного переменного Z(x). Указан диапазон изменения переменной х (нижняя граница d и верхняя граница D). Видно, что абсолютный минимум функции соответствует точке 1, а относительный минимум – точке 2, принадлежащей заданному диапазону изменения переменной х.
|
|
|
Рис. 1.2. Абсолютный (точка 1) и относительный (точка 2) минимумы функции
B.3. Линейные оптимизационные задачи
Если целевая функция и система ограничений являются линейно зависимыми от переменных х 1, х 2 ,... хn, для решения оптимизационной задачи используются методы линейного программирования.
Линейная математическая модель в общем случае имеет следующий вид:
Z = z 1 x 1 +z 2 x 2 +...+znxn → extr,
a 11 x 1 +a 12 x 2 +...+a 1n xn < b 1,
a 21 x 1 +a 22 x 2 +...+a 2 n xn = b2,
........................
a m1 x 1 +am2x2+...+amnxn > bm,
хi > 0, i = 1, 2, ... n,
где zi, bj, aji - заданные постоянные величины, i = 1.2,… n; j = 1, 2,... m.
Задача линейного программирования формулируется следующим образом: найти экстремальное значение линейной целевой функции Z при ограничениях, заданных в форме линейных равенств и (или) неравенств, и граничных условиях, указывающих диапазон изменения переменных.
В реальных оптимизационных задачах ищется или минимум или максимум целевой функции. Методы линейного программирования работают совершенно одинаково, как при поиске минимума целевой функции, так и при поиске ее максимума.
Допустим, что в линейной математической модели (2.1) ищется минимум целевой функции
Z = z 1 x 1 +z2x2+...+znxn → min.
Если по этой же математической модели нужно найти максимум целевой функции Z, то у коэффициентов целевой функции меняются знаки на противоположные и вновь ищется минимум функции Z
Z = - z 1 x 1 - z 2 x 2 -...- znxn → min.
Таким образом, min (- z 1 x 1- z 2 x 2 -…- znxn) = max (z 1 x 1+ z 2 x 2+ …+ znxn)
Порядок выполнения.
Пример. Решить задачу линейного программирования:
L = 5x1 - 2x3 ®min
- 5x1 - x2 + 2x3 ≤ 2
- x1+x3 + x4 ≤ 5
- 3x1 + 5x4 ≤ 7
x1, x2, x3, x4 – целые
0≤xi≤100, iÎ1,2…4
Для решения подобных задач в MS EXCEL предназначена команда Поиск решения из меню Сервис.
Пусть значения x1, x2, x3, x4 хранятся в ячейки A1:A4, a значение функции L - в ячейке С1.
Введем целевую функцию:
С1 = –5*A1 – 2*A3
Введем ограничения:
С2 = –5*A1 - A2 + 2*A3
С3 = –А1 +А3 + А4
С4 = –3*А1 + 5*А4.
Пример заполнения экранной формы в MS Excel показан на рис. 1.

Рисунок. 1.
Таким образом, было задано условие исходной задачи линейного программирования. Выполним команду из главного меню Сервис ® Поиск решения (рис. 1).
|
|
|

Рисунок. 2.
Устремим целевую функцию в ячейке C1 к минимуму. Для этого введем в поле Установить целевую функцию значение С1 и установим опцию " равной минимальному значению ". В поле Изменяя ячейки необходимо указать адреса ячеек, в которых хранятся изменяемые значения. В нашем случае это ячейки А1:А4.
Для добавления ограничений необходимо щелкнуть по кнопке Добавить, появится диалоговое окно Добавить ограничение (рис. 2)

Рисунок. 3.
В поле ввода Ссылка на ячейку необходимо ввести адрес ячейки, где хранится ограничение, затем, щелкнув по стрелке, выбрать знак и ввести значение ограничения в поле Ограничение.
Щелчок по кнопке OK означает ввод очередного ограничения и возврат к диалоговому окну Поиск решения.
Щелчок по кнопке Добавить вводить очередное ограничение, находясь в окне Добавить ограничение.
В нашем случае окно будет иметь вид, изображенный на рис. 3. Щелчок по кнопке Выполнить начнет процесс решения задачи, завершится который появлением диалогового окна, изображенного на рис. 4.

Рисунок. 4.

Рисунок. 5.
Щелчок по кнопке OK приведет к появлению в ячейке С1 значения целевой функции L, а в ячейках A1:A4 - значений переменных x1-x4, при которых целевая функция достигает минимального значения (рис. 6).

Рисунок. 6.
Если задача не имеет решения или неверно были заданы исходные данные, в окне Результаты поиска решения может появиться сообщение о том, что решение не найдено.
Итак, назначение основных кнопок и окон диалогового окна Поиск решения:
· Поле Установить целевую ячейку - определяет целевую ячейку, значение которой необходимо максимизировать или минимизировать, или сделать равным конкретному значению.
· Опции " минимальному значению ", " максимальному значению " и " значению ", определяют, что необходимо сделать со значением целевой ячейки - максимизировать, минимизировать или сделать равным конкретному значению.
· Поле Изменяя ячейки определяет изменяемые ячейки. Изменяемая ячейка - это ячейка, которая может быть изменена в процессе поиска решения для достижения нужного результата в ячейке из окна Установить целевую ячейку с удовлетворением поставленных ограничений.
· Кнопка Предположить отыскивает все неформульные ячейки, прямо или непрямо зависящие от формулы в окне Установить целевую ячейку, и помещает их ссылки в окно Изменяя ячейки.
· Окно Ограничения перечисляет текущие ограничения в данной задаче. Ограничение есть условие, которое должно удовлетворяться решением. Ограничения перечисляются в виде ячеек или интервалов ячеек, обычно содержащих формулу, которая зависит от одной или нескольких изменяемых ячеек, чье значение должно попадать внутрь определенных границ или удовлетворять равенству.
|
|
|
· кнопки Добавить, Изменить, Удалить позволяют добавить, изменить или удалить ограничение.
· Кнопка Выполнить запускает процесс решения определенной задачи.
· Кнопка Закрыть закрывает окно диалога, не решая проблемы. Сохраняются лишь изменения, сделанные при помощи кнопок Параметры, Добавить, Изменить и Удалить. Не сохраняются изменения, произведенные после использования данных кнопок.
· Кнопка Параметры выводит окно диалога Параметры поиска решения, в котором можно контролировать различные аспекты процесса отыскания решения, а также загрузить или сохранить некоторые параметры, такие, как выделение ячеек и ограничений, для какой-то конкретной задачи на рабочем листе.
· Кнопка Сбросить очищает все текущие установки задачи и возвращает все параметры к их значениям по умолчанию.
С помощью решающего блока можно решить множество различный оптимизационных задач (задач на максимум и минимум) с ограничениями любого типа. При решении задачи целочисленного программирования необходимо добавить ограничение, показывающее, что переменные целочисленные. При решении других оптимизационных задач вводят целевую функцию и ограничения.
В задачах линейного программирования всегда необходимо найти минимум (или максимум) линейной функции многих переменных при линейных ограничениях в виде равенств или неравенств.
В задачах линейного программирования всегда необходимо найти минимум (или максимум) линейной функции многих переменных при линейных ограничениях в виде равенств или неравенств.

В задачи целочисленного программирования добавляется ограничение, что все xi должны быть целыми.
ЗАДАНИЕ
1. Найти решение, которое дает минимум целевой функции.
2. Найти решение, которое дает максимум целевой функции.
3. Найти решение, при котором целевая функция равна N (N – номер варианта).
4. Повторить пункты №1-3, если x1, x2, x3, x4 – целые числа.
Примечание. Принять для пунктов 1-3, что x1, x2, x3, x4 положительные числа.
ВАРИАНТЫ ЗАДАНИЙ

| 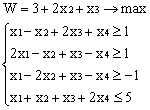
| ||

| 
| ||

| 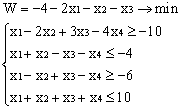
| ||

| 
| ||
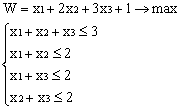
| 
| ||

| 
| ||

| 
| ||
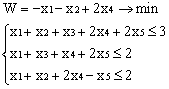
| 
| ||
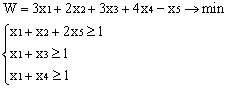
| 
| ||

| 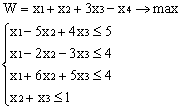
| ||

| 
| ||

| 
| ||

| 
| ||

| 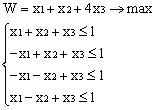
| ||

| 
|
Контрольные вопросы:
1. Что такое критерий оптимальности? Привести примеры для электроэнергетики.
2. Перечислить и описать этапы решения оптимизационных задач.
3. Перечислить и описать составляющие математической модели оптимизации.
4. Описать, что представляет собой класс задач линейного программирования.
|
|
|


