 |
Метод Гаусса с частичным выбором ведущего элемента
|
|
|
|
Лекция 2
Метод Гаусса
§ 2. Метод Гаусса [1]
Простой пример применения метода
Освоение любой проблемы проще всего начать с разбора простого примера. Рассмотрим систему трех линейных уравнений:
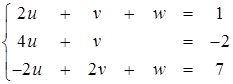(2.1)
Решение его по методу Гаусса или, как его еще называют, методу исключения состоит в последовательном исключении неизвестных.
1-й шаг: исключение u из 2-го и 3-го уравнений. Для этого, как нетрудно убедиться, можно вычесть из второго уравнения первое, умноженное на 2, а третье уравнение сложить с первым:
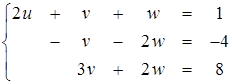(2.2)
2-й шаг: исключение v из 3-го уравнения. Для этого второе уравнение умножаем на 3 и складываем с последним, третьим:
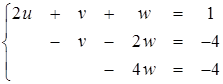(2.3)
3-й шаг: решение треугольной системы. Треугольный вид (2.3), к которому приведена система (2.1), позволяет легко определить неизвестные, двигаясь от нижней строки системы к верхней:
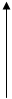
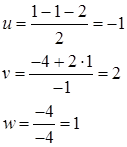(2.4)
Формулировка метода Гаусса для произвольной системы
Таким образом, метод Гаусса для системы линейных уравнений порядка n:
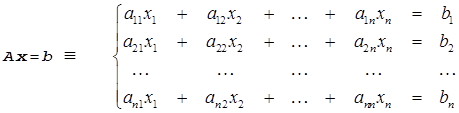(2.5)
можно описать следующим образом:
1. Первое уравнение системы остается без изменений, а из остальных исключается первое неизвестное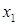 
. Это достигается вычитанием из второго уравнения первого уравнения, умноженного на 
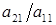; из третьего уравнения - первого уравнения, умноженного на 
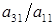;...; из n -го уравнения ‑ первого уравнения, умноженного на 
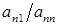. В результате этого исключения система (2.5) приводится к виду
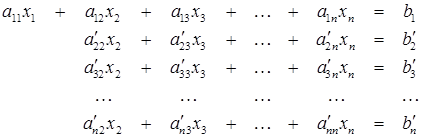(2.6)
Отметим, что последние (n-1) уравнений образуют систему (n-1) уравнений с (n-1) неизвестными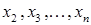 
. Штрих при коэффициентах 
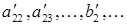и т.д. напоминает нам о том, что эти величины отличаются от исходных 
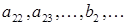из (2.5). Конечно, мы могли бы в системе (2.6) указать точные значения этих величин, например, 
. Однако это сделало бы нашу простую схему загроможденной буквами и знаками операций и, поэтому, малопонятной.
|
|
|
2. Далее поступаем с нижними (n-1) строками системы (2.6) так же, как поступили со всей системой на первом этапе. В результате (2.6) приводится к виду
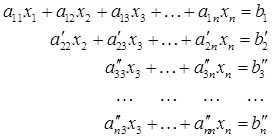(2.7)
Здесь два штриха в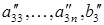 
и т.д. напоминают о том, что эти величины получены после исключения второй неизвестной. И в дальнейшем новое значение коэффициента 
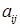или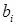 
, полученное после исключения k -й неизвестной, будем обозначать 
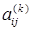или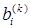 
. Продолжаем процесс исключения для 
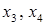и т.д. до тех пор, пока не будет исключено 
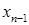из n -го уравнения. В результате исходная система будет приведена к треугольному виду:
(2.8)
3. Обратный ход. Из последнего уравнения (2.8), в котором лишь одна неизвестная, легко определяем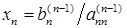 
. В предпоследнем уравнении две неизвестных, одну из которых мы уже успели определить. Поднимаясь, таким образом, со строки на строку системы (2.8), мы очень просто определяем одну за другой неизвестные 
.
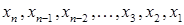Здесь наступил подходящий момент ввести понятие ведущего элемента. Ведущим элементом системы линейных уравнений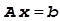 
или матрицы A называются первые ненулевые коэффициенты системы, полученные после гауссова исключения. В (2.8) такими ведущими элементами являются 
.
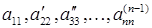Метод Гаусса с частичным выбором ведущего элемента
Итак, метод Гаусса выглядит предельно простым. Однако известно, что любая работа кажется простой, если ее не надо выполнять самому. Но стоит только начать копать яму, красить забор … или решать систему линейных уравнений, как одна за другой начинают возникать трудности, которые до того и в голову не приходили. Какие же подводные камни подстерегают нас при применении метода Гаусса?
Попробуем решить такую систему
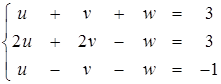(2.9)
В соответствии с нашим описанием алгоритма исключаем первую неизвестную u из второго и третьего уравнений. Для этого вычитаем из второго уравнения первое уравнение, умноженное на 2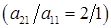 
, а из третьего уравнения ‑ первое 
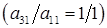. В результате получаем
|
|
|
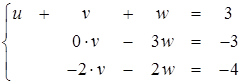(2.10)
Если теперь мы продолжим бездумно следовать описанной схеме, то, попытавшись вычесть из третьего уравнения второе, умноженное на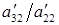 
, мы обнаружим, что пытаемся выполнить невозможную операцию деления на ноль 
.
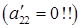Нетрудно догадаться, как можно обойти это препятствие в данном случае. Если в (2.10) поменять местами вторую и третью строки, то для полученной системы
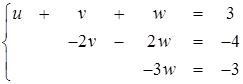(2.11)
мы можем продолжить решение по методу Гаусса без каких-либо новых неприятностей.
Чтобы исключить возможность возникновения такой ситуации, алгоритм Гаусса нуждается в некоторой доработке. Идея состоит в следующем. Как известно из разд. 2.2, после исключения k -го неизвестного система уравнений принимает вид
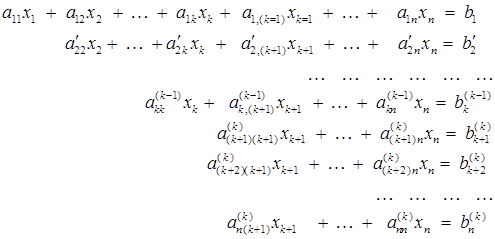(2.12)
Понятно, что строки с (k+1) -й по n -ю системы (12) можно переписать в любом порядке. Это никак не скажется на решении. Мы уже научены горьким опытом, как неприятно обнаружить на месте ведущего элемента ноль. Поэтому имеет смысл перестраховаться и переписать в (k+1) -ю строку то из оставшихся уравнений, в котором коэффициент при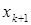 
имеет самую большую абсолютную величину.
Итак, сформулируем окончательно, в чем заключается метод Гаусса с частичным выбором ведущего элемента:
Перед каждым новым шагом исключения необходимо сравнить ведущий элемент со всеми другими возможными ведущими элементами. Затем переставить уравнения таким образом, чтобы новым ведущим элементом стал наибольший по модулю из рассмотренных кандидатов.
Именно с этим уточнением метод Гаусса используется в программах, разработанных для компьютеров.
|
|
|
12 |
