 |
Приведение симметричной матрицы к трехдиагональной форме (преобразование Хаусхолдера)
|
|
|
|
Лекция 12
QR-алгоритм
§ 13. Ортогонализация системы векторов по методу Грама ‑ Шмидта
 |
Базисом линейного пространства может служит любая система векторов, лишь бы эти вектора были независимы. Однако (см рис. 13.1) гораздо удобнее пользоваться таким базисом, компоненты которого ортогональны между собой. Еще лучше, когда все вектора базиса имеют одинаковую длину, равную единице. Рис. 13.1 иллюстрирует это высказывание для двумерного случая, но конечно это справедливо и для пространства произвольной размерности. Со школьной скамьи мы привыкли пользоваться ортонормированным базисом (декартовы координаты), даже не подозревая, что возможны иные варианты.
Поэтому часто практически важной оказывается следующая задача. Имеется система линейно независимых векторов 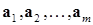 . Требуется построить ортонормированную систему векторов
. Требуется построить ортонормированную систему векторов  равноценную исходной. Равноценность понимается следующим образом: если какой-либо вектор можно представить в виде разложения по векторам
равноценную исходной. Равноценность понимается следующим образом: если какой-либо вектор можно представить в виде разложения по векторам 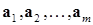 , то его можно представить и в виде разложения по
, то его можно представить и в виде разложения по  и наоборот.
и наоборот.
Для решения этой задачи и предназначен метод ортогонализации Грама ‑ Шмидта, который заключается в следующем.
 Итак, имеем
Итак, имеем  векторов
векторов 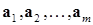 . В качестве первого вектора
. В качестве первого вектора  новой ортогональной системы (пока не нормированной) резонно выбрать
новой ортогональной системы (пока не нормированной) резонно выбрать  . Чтобы получить второй вектор, рассмотрим следующую картинку (рис. 13.2). Вектор
. Чтобы получить второй вектор, рассмотрим следующую картинку (рис. 13.2). Вектор  можно рассматривать как сумму двух слагаемых: первое из них совпадает по направлению с
можно рассматривать как сумму двух слагаемых: первое из них совпадает по направлению с  , а второе перпендикулярно
, а второе перпендикулярно  . В качестве второго вектора
. В качестве второго вектора  ортогональной системы выбирается, естественно, второе слагаемое:
ортогональной системы выбирается, естественно, второе слагаемое:
 . (13.1)
. (13.1)
Третий вектор  находим аналогично, вычитая из
находим аналогично, вычитая из  его проекции на
его проекции на  и
и  :
:
|
|
|
 . (13.2)
. (13.2)
Продолжая этот процесс, каждый очередной вектор  находим, вычитая из
находим, вычитая из  его проекции на
его проекции на  :
:
 . (13.3)
. (13.3)
После того как будут найдены все  , остается только нормировать их:
, остается только нормировать их:
 . (13.4)
. (13.4)
Пример. Выполним ортогонализацию Грама - Шмидта для векторов
 .
.
Сначала строим систему ортогональных векторов
 ;
;
 ;
;
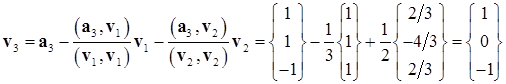 .
.
Затем нормируем их
 ;
;
 ;
;
 .
.
При желании нетрудно проверить, что полученные вектора нормированы 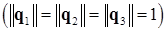 и ортогональны
и ортогональны 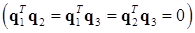 .
.
Замечание. Выражение (13.3) иногда удобнее использовать в таком виде:
 (13.5)
(13.5)
Для этого используются очевидные соотношения:  и
и  . При использовании (13.5) в ходе ортогонализации, разумеется, вычисление очередного ортонормированного вектора
. При использовании (13.5) в ходе ортогонализации, разумеется, вычисление очередного ортонормированного вектора  надо выполнять сразу после определения очередного ортогонального (но не нормированного) вектора
надо выполнять сразу после определения очередного ортогонального (но не нормированного) вектора  . А не откладывать это до определения всех
. А не откладывать это до определения всех  , а не откладывать это до определение всех
, а не откладывать это до определение всех  .
.
Сведения о QR-алгоритме
Достаточно полную информацию об этом методе в рамках столь краткого курса дать невозможно, однако целесообразно привести хотя бы краткие сведения, так как QR-алгоритм на сегодня является наиболее эффективным средством для решения полной проблемы собственных значений. Прежде чем приступить к рассмотрению метода, советуем освежить в памяти понятия скалярного произведения, ортогональности, линейной зависимости векторов, базиса  -мерного пространства. Обязательно надо иметь четкое представление об ортогонализации системы векторов по методу Грама – Шмидта (см, например, [12.1]).
-мерного пространства. Обязательно надо иметь четкое представление об ортогонализации системы векторов по методу Грама – Шмидта (см, например, [12.1]).
QR-разложение матрицы
Вспомнив эти сведения, рассмотрим произвольную матрицу
 (14.1)
(14.1)
и отметим, что ее можно рассматривать как совокупность  векторов-столбцов
векторов-столбцов  . Применим к этим векторам метод Грама ‑ Шмидта:
. Применим к этим векторам метод Грама ‑ Шмидта:
 (14.2)
(14.2)
Очевидно, что (2) можно переписать таким образом:
 (14.3)
(14.3)
Заметим, что система (14.3) есть не что иное, как матричное равенство:
 (14.4)
(14.4)
 |
 ,
,
где  – ортогональная матрица, а
– ортогональная матрица, а  – верхняя (или, иначе говоря, правая) треугольная матрица.
– верхняя (или, иначе говоря, правая) треугольная матрица.
|
|
|
Замечание 1. Процесс ортогонализации столбцов матрицы  мы начали с первого столбца
мы начали с первого столбца  . Между тем последний столбец
. Между тем последний столбец  ничем не хуже. Если процесс ортогонализации начать с последнего столбца
ничем не хуже. Если процесс ортогонализации начать с последнего столбца  и последовательно ортогонализировать столбцы в обратном порядке:
и последовательно ортогонализировать столбцы в обратном порядке:  , можно получить аналогичное, но несколько отличающееся от (14.4) разложение матрицы
, можно получить аналогичное, но несколько отличающееся от (14.4) разложение матрицы  :
:
 , где
, где  . (14.5)
. (14.5)
Такое разложение носит название QL-разложения. С чисто теоретической точки зрения оба эти разложения равноценны. При практическом применении есть небольшие отличия, о которых будет сказано в следующем пункте. Чтобы не путаться в названиях QL и QR, обратите внимание на то, что слово Left означает «левый», а Right – «правый».
Замечание 2. Обратите внимание на то, что (14.4) и (14.5) определяют еще один способ решения систем линейных уравнений. В самом деле, подставляя в систему линейных уравнений 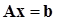 вместо матрицы
вместо матрицы  ее разложение и, учитывая ортогональность матрицы
ее разложение и, учитывая ортогональность матрицы  , можно привести эту систему к треугольному виду:
, можно привести эту систему к треугольному виду:
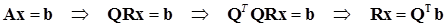 . (14.6)
. (14.6)
QR-алгоритм
Теперь, уяснив, как строится QR-разложение матрицы, можно перейти к изложению QR-алгоритма:
1) сначала выполняется QR-разложение исходной матрицы  . Полученные матрицы
. Полученные матрицы  и
и  используются для вычисления первого приближения следующим образом:
используются для вычисления первого приближения следующим образом:  . Обратите внимание, что матрица
. Обратите внимание, что матрица  и исходная матрица
и исходная матрица  подобны:
подобны:
 ;
;
2) второе приближение определяется аналогично:
 ;
;
3) продолжая этот процесс, получаем последовательность матриц  , которая в случае симметричной матрицы
, которая в случае симметричной матрицы  сходится к диагональной матрице.
сходится к диагональной матрице.
Доказательство сходимости QR-алгоритма не приводим. Интересующиеся могут ознакомиться с ним в [12.2]. Здесь ограничимся рассмотрением уже хорошо знакомого примера:
Пример.
0) 
1) 
2) 
3)  .
.
Существует и применяется практически QL-алгоритм, полностью аналогичный QR-алгоритму. Единственное важное отличие заключается в том, что при применении QR-алгоритма наименьшие собственные значения оказываются внизу, а при применении QL-алгоритма ‑ вверху.
Приведение симметричной матрицы к трехдиагональной форме (преобразование Хаусхолдера)
QR-алгоритм в чистом виде, так как он описан в разделе 14.2, сходится довольно медленно. Дело в том, что на каждом шаге требуется сначала провести ортогонализацию Грама ‑ Шмидта для системы  векторов, а затем перемножить две матрицы размера
векторов, а затем перемножить две матрицы размера  . На выполнение этих операций требуется довольно много арифметических действий и, как следствие, машинного времени. Во всяком случае, метод Якоби, рассмотренный ранее, решает задачу гораздо быстрее.
. На выполнение этих операций требуется довольно много арифметических действий и, как следствие, машинного времени. Во всяком случае, метод Якоби, рассмотренный ранее, решает задачу гораздо быстрее.
|
|
|
Тем не менее, именно QR-алгоритм на сегодняшний день является самым эффективным средством для решения полной задачи о собственных значениях. (Под полной задачей понимается задача определения всех собственных значений матрицы и, при необходимости, всех собственных векторов.) Дело в том, что на практике QR-алгоритм применяется не сразу к исходной матрице, а после предварительной подготовки: исследуемая матрица  приводится к подобной трехдиагональной матрице:
приводится к подобной трехдиагональной матрице:
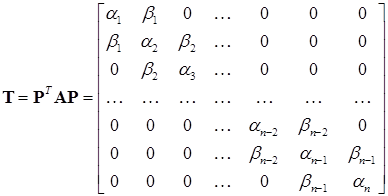 . (14.7)
. (14.7)
Именно для трехдиагональных матриц QR-алгоритм обладает наибольшей эффективностью. Вопрос об организации вычислений для трехдиагональных матриц будет рассмотрен в разделе 14.4. Здесь разберемся, каким образом произвольную симметричную матрицу  можно привести к подобной ей трехдиагональной матрице
можно привести к подобной ей трехдиагональной матрице  .
.
Подобно тому, как в методе Якоби используется специальный инструмент – матрицы вращений (§ 12, формула (12.8)), так и для приведения симметричной матрицы к трехдиагональной форме используются так называемые матрицы Хаусхолдера:
 , (14.8)
, (14.8)
где  – единичная матрица, а
– единичная матрица, а 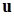 – некоторый вектор.
– некоторый вектор.
Заметим, что матрица Хаусхолдера симметрична
 (14.9)
(14.9)
и ортогональна
 (14.10)
(14.10)
Кстати, обратите внимание на то, что если произведение векторов
 (14.11)
(14.11)
представляет собой число (скалярное произведение), то произведение
 (14.12)
(14.12)
является матрицей размера  .
.
Матрица Хаусхолдера обладает двумя полезными свойствами:
1) для того чтобы запомнить матрицу (14.8), не надо запоминать  элементов, но достаточно занести в память
элементов, но достаточно занести в память  элементов вектора
элементов вектора 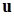 ;
;
2) для любого вектора  произведение
произведение  будет представлять собой вектор, у которого от нуля отличен только один первый элемент:
будет представлять собой вектор, у которого от нуля отличен только один первый элемент:
 , (14.13)
, (14.13)
если в качестве вектора  при определении матрицы
при определении матрицы  (см. формулу (14.8)) взять вектор
(см. формулу (14.8)) взять вектор
|
|
|
 . (14.14)
. (14.14)
Доказательство
 (14.15)
(14.15)
Теперь, выяснив основные свойства матрицы  , можно перейти к приведению матрицы
, можно перейти к приведению матрицы  к трехдиагональному виду. Рассмотрим матрицу
к трехдиагональному виду. Рассмотрим матрицу  , мысленно разделив ее на блоки:
, мысленно разделив ее на блоки:
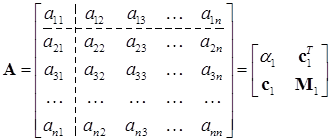 . (14.16)
. (14.16)
Здесь введены обозначения:
 . (14.17)
. (14.17)
Теперь составим следующую ортогональную матрицу:
 , (14.18)
, (14.18)
где  – матрица Хаусхолдера размера
– матрица Хаусхолдера размера 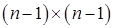 , причем вектор
, причем вектор 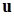 для ее образования выберем следующим образом:
для ее образования выберем следующим образом:
 . (14.19)
. (14.19)
Как было выяснено при рассмотрении свойств матрицы Хаусхолдера,
 . (14.20)
. (14.20)
Теперь, имея на вооружении соотношение (14.20), попробуем выполнить следующее преобразование подобия:
 . (14.21)
. (14.21)
Во-первых, учтем, что матрица  симметрична, т.е.
симметрична, т.е. 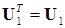 , во-вторых, перепишем (14.21) подробнее, с учетом блочной структуры матриц
, во-вторых, перепишем (14.21) подробнее, с учетом блочной структуры матриц  и
и  :
:
 . (14.22)
. (14.22)
Выполняя перемножение 1-й и 2-й матрицы в (14.22), получаем
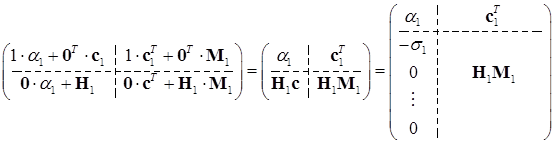 .
.
(14.23)
Второе умножение в (14.22)

(14.24)
приводит к матрице, подобной  , для которой в первом столбце достигнут требуемый результат – все элементы, кроме диагонального и поддиагонального, равны нулю. Кстати, аналогичный эффект получен и в первой строке.
, для которой в первом столбце достигнут требуемый результат – все элементы, кроме диагонального и поддиагонального, равны нулю. Кстати, аналогичный эффект получен и в первой строке.
На следующем шаге формируем матрицу
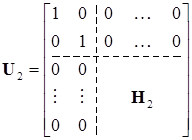 , (14.25)
, (14.25)
при этом вектор 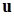 размерности
размерности 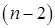 , необходимый для построения матрицы Хаусхолдера, выбирается так же, как это делалось на первом шаге, но уже по отношению к полученной после первого шага подматрице
, необходимый для построения матрицы Хаусхолдера, выбирается так же, как это делалось на первом шаге, но уже по отношению к полученной после первого шага подматрице  , т.е.
, т.е.
 (14.26)
(14.26)
После выполнения второго преобразования
 (14.27)
(14.27)
требуемый результат будет получен уже для первых двух строк и столбцов матрицы. Нетрудно убедиться, что после 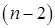 преобразований исходная матрица
преобразований исходная матрица  будет приведена к подобной ей трехдиагональной матрице
будет приведена к подобной ей трехдиагональной матрице
 (14.28)
(14.28)
При оценке трудоемкости приведения (14.28) необходимо иметь в виду, что нет никакой необходимости строить матрицы  в явном виде. Достаточно получать на каждом шаге вектора
в явном виде. Достаточно получать на каждом шаге вектора  соответственно с размерностями
соответственно с размерностями  . При выполнении преобразования
. При выполнении преобразования
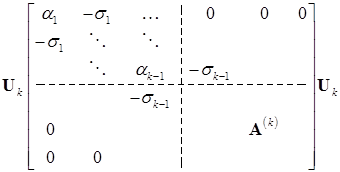 (14.29)
(14.29)
элементы  , полученные на предыдущих шагах, остаются без изменений;
, полученные на предыдущих шагах, остаются без изменений; 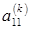 – верхний левый элемент блока
– верхний левый элемент блока  также остается без изменений; элементы первого столбца и первой строки блока
также остается без изменений; элементы первого столбца и первой строки блока  :
:  заменяются на
заменяются на  , где
, где  , а для вычисления
, а для вычисления  – блока размерности
– блока размерности  получим выражение, использующее только вектор
получим выражение, использующее только вектор  , но не матрицу
, но не матрицу  . Вспомним сначала, что матрицу
. Вспомним сначала, что матрицу  мы представляем в блочном виде:
мы представляем в блочном виде:
 . (14.30)
. (14.30)
Поэтому для нижнего правого блока можно получить следующее выражение:
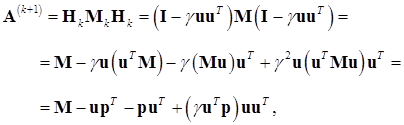 (14.31)
(14.31)
где
 . (14.32)
. (14.32)
В (14.31) и (14.32) индекс  при
при  опущен, чтобы не перегружать формулы.
опущен, чтобы не перегружать формулы.
Пример. Выполнить приведение к трехдиагональному виду матрицы
 .
.
Как нам известно, для приведения этой матрицы потребуется выполнить  преобразования Хаусхолдера.
преобразования Хаусхолдера.
Первое преобразование
 ;
;
 ,
,  ,
, 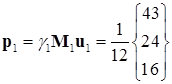 ,
,
 .
.
Используя полученные значения, можем заполнить матрицу – результат первого преобразования:
|
|
|
 .
.
Второе преобразование

 ,
,
следовательно,

|
|
|


