Приведение симметричной матрицы к трехдиагональному виду

В рассмотренном выше методе итераций в подпространстве использовалась система векторов. Выбор этих векторов осуществлялся, вообще говоря, произвольно. Т.е. этот выбор никак не зависел от свойств исследуемой матрицы .

Вспомним также, что использование процедуры Рэлея ‑ Ритца для корректировки системы векторов значительно повысило скорость сходимости метода. Отметим, что эта процедура использует матрицу , которая содержит некоторую, хотя и урезанную, информацию о матрице .

В связи с этим естественной выглядит попытка при выборе исходной системы векторов каким-то образом использовать свойства исследуемой матрицы . Желательно также, чтобы для такого выбора не нужна была матрица в явном виде, но достаточно иметь правило (программу), позволяющее определить произведение для произвольного вектора . Это ограничение связано с тем, что для очень больших матриц иная форма их определения часто оказывается невозможной.

Наилучшим известным на сегодня выбором такой системы являются вектора следующего вида:

, (18.1)

где первый вектор выбирается произвольно, а все остальные вектора уже несут в себе информацию об исследуемой матрице .

Система векторов (18.1) порождает векторное пространство размерности . Напомним, что линейным подпространством, порожденным системой векторов , называется множество всех векторов , которые можно представить в виде линейной комбинации:

. (18.2)

Кстати, короче такое подпространство часто называется линейной оболочкой векторов . Линейные оболочки системы векторов вида (18.1) и называются подпространствами Крылова по имени советского академика, впервые использовавшего их для решения практических задач.

Система векторов хороша тем, что сами вектора этой системы содержат информацию о матрице . Однако у нее есть серьезный недостаток – эти вектора неортогональны.

Поясним это геометрической иллюстрацией (рис. 18.1). В результате первого умножения будет получен вектор, который повернут относительно исходного вектора на некоторый угол. Вновь умножая полученный вектор на матрицу , получаем следующий вектор , который также повернут на некоторый угол по отношению к предыдущему вектору. Из рассмотренного ранее степенного метода нам известно, что вектор при стремится к собственному вектору, соответствующему максимальному собственному значению. Таким образом, с ростом направление очередного вектора все меньше будет отличаться от направления предыдущего. На рис.18.1 это направление обозначено пунктирной линией.

Нам уже известно средство для «исправления» таких систем векторов – алгоритм Грама ‑ Шмидта. Применив его к системе можно получить равноценную систему векторов , но уже с ортогональными единичными векторами. Как мы сейчас увидим, алгоритм Грама ‑ Шмидта, вообще говоря, весьма трудоемкий, значительно упрощается для системы векторов .

Найдем несколько первых векторов этой ортогональной системы.

Первый вектор

1) обозначим исходный вектор (зерно подпространства) ;

2) длину этого вектора обозначим ;

3) тогда для получения первого вектора надо только нормировать исходный вектор:

. (18.2)

Второй вектор

1) вычисляем очередной вектор Крылова:

; (18.3)

2) вычитаем из этого вектора составляющую в направлении :

. (18.4)

Здесь введено обозначение:

. (18.5)

Отметим, что для вычисления не надо полностью вычислять значение квадратичной формы 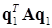, но можно просто вычислить скалярное произведение векторов и , определенных на предыдущих шагах;

3) определяем длину вектора :

; (18.6)

4) нормируя вектор , получаем второй вектор ортогональной системы:

. (18.7)

Третий вектор

1) вычисляем очередной вектор Крылова:

; (18.8)

2) вычитаем из этого вектора составляющие в направлении и :

. (18.9)

Вновь обозначим

. (18.10)

Что касается произведения , то следует отметить, что согласно (18.8)

. (18.11)

Кроме того, учитывая, что согласно (18.7)

,

и в соответствии с (18.3) и (18.4)

,

получим

, (18.12)

т.е. специально вычислять это произведение не надо. Оно уже вычислено на предыдущем шаге.

Итак, окончательно для получаем

; (18.13)

3) вычисляем длину вектора

, (18.14)

которая, как нам уже известно, понадобится и на следующем шаге;

4) . (18.15)

Четвертый вектор :

1) ;

2) .

Здесь необходимо заметить, что . Вспомним, что при построении мы представили как сумму двух составляющих: одна направлена вдоль , другая вдоль , т.е.

,

где и – некоторые коэффициенты. Следовательно,

вследствие взаимной ортогональности векторов . Следовательно,

.

Это очень важный момент, определяющий в конечном счете эффективность и популярность метода Ланцоша: для определения вектора используются вектора и , но не нужен вектор !

Такие же рассуждения можно привести и для произвольного -го вектора – для его определения используются и и не нужны остальные вектора ;

3) ;

4) .

Теперь мы готовы сформулировать алгоритм построения ортонормированного базиса подпространства Крылова:

Задаемся произвольным начальным вектором длиной . Если уже определены вектора , то очередной вектор определяется следующим образом:

1. ; 2. ; 3. ; 4. ; 5. .

Для практического усвоения этого алгоритма полезно рассмотреть следующий пример.

Пример. Рассмотрим построение ортогонального базиса подпространства Крылова для матрицы

.

В качестве начального вектора («зерна») берем

.

Определяем :

.

Определяем :

.

Определяем :

,

.

Определяем :

, ,

.