 |
Задачи, приводящие к проблеме собственных значений
|
|
|
|
Лекция 10
Проблема собственных значений
Часть III. Алгебраическая проблема собственных значений
Задачи, приводящие к проблеме собственных значений
Задача о собственных значениях возникает не только в задачах механики. В частности, к ней приводят математические модели явлений в таких научных дисциплинах, как геометрия, астрономия, физика. Второе название характеристического уравнения ‑ вековое уравнение ‑ связано с тем, что это уравнение встречается при исследовании вековых возмущений движения планет. В данном пособии рассматривается задача о собственных значениях:
 (10.1)
(10.1)
только для случая, когда матрица  симметрична и положительно определена. Это ограничение связано с тем, что в задачах механики, приводящим к проблеме собственных значений, в подавляющем большинстве случаев матрицы жесткости и матрицы масс механических систем являются именно симметричными и положительно определенными. Причины этого уже обсуждались в третьей лекции.
симметрична и положительно определена. Это ограничение связано с тем, что в задачах механики, приводящим к проблеме собственных значений, в подавляющем большинстве случаев матрицы жесткости и матрицы масс механических систем являются именно симметричными и положительно определенными. Причины этого уже обсуждались в третьей лекции.
 Как возникает проблема собственных значений в задачах механики? Разберем подробно этот вопрос на примере двухстепенной механической системы, изображенной на рис. 10.1. Эта система представляет собой два одинаковых груза, соединенных между собой и с неподвижными опорами при помощи трех одинаковых невесомых пружин.
Как возникает проблема собственных значений в задачах механики? Разберем подробно этот вопрос на примере двухстепенной механической системы, изображенной на рис. 10.1. Эта система представляет собой два одинаковых груза, соединенных между собой и с неподвижными опорами при помощи трех одинаковых невесомых пружин.
Составим уравнения движения этой системы. Чаще всего для этого самым удобным способом является использование уравнений Лагранжа второго рода:
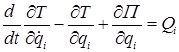
 , (10.2)
, (10.2)
где  – количество степеней свободы системы;
– количество степеней свободы системы;  – обобщенные координаты;
– обобщенные координаты;  – обобщенные силы;
– обобщенные силы;  – кинетическая и потенциальная энергии системы.
– кинетическая и потенциальная энергии системы.
Потенциальная энергия системы складывается из потенциальных энергий трех пружин:
|
|
|
 (10.3)
(10.3)
Кинетическая энергия системы складывается из кинетических энергий двух грузов:
 . (10.4)
. (10.4)
Здесь мы рассматриваем собственные колебания системы, следовательно,  .
.
Согласно (10.2), (10.3) и (10.4) слагаемые первого уравнения Лагранжа для данной системы будут:
 (10.5)
(10.5)
следовательно, первое уравнение имеет вид
 (10.6)
(10.6)
Аналогично получаем второе уравнение
 (10.7)
(10.7)
Выпишем оба уравнения в виде системы:
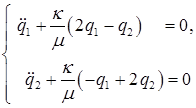 (10.8)
(10.8)
или в матричном виде
 , (10.9)
, (10.9)
где
 . (10.4)
. (10.4)
Решение уравнения (10.9), как положено (см, например, [10.1]), будем искать в виде
 . (10.11)
. (10.11)
В результате подстановки (10.11) в (10.9) получим
 . (10.12)
. (10.12)
Если обозначить  , то нетрудно заметить, что (10.12) полностью совпадает с (10.1).
, то нетрудно заметить, что (10.12) полностью совпадает с (10.1).
Итак, на простом примере (рис. 10.1) мы увидели, каким образом в задачах механики может возникать задача о собственных значениях. Осталось разобраться, как можно эту задачу решать, и каков физический смысл полученного решения. Уравнение (10.12) несложно привести к следующему виду:
 . (10.13)
. (10.13)
Полученная однородная система линейных уравнений (правые части равны нулю), согласно одной из основных теорем линейной алгебры (см, например, [10.2]), имеет ненулевые решения тогда и только тогда, когда определитель этой системы равен нулю:
 (10.14)
(10.14)
Уравнение (10.14) называется характеристическим уравнением матрицы  и решение его сводится к отысканию корней полинома
и решение его сводится к отысканию корней полинома  -й степени.
-й степени.
В рассмотренном выше примере (10) характеристическое уравнение
 (10.15)
(10.15)
является квадратным уравнением:
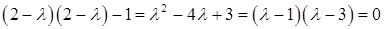 (10.16)
(10.16)
и имеет два корня:  , которые и являются собственными значениями. Кстати, если вы сами еще этого не заметили, отметим, что для упрощения вычислений мы положили в (10.10)
, которые и являются собственными значениями. Кстати, если вы сами еще этого не заметили, отметим, что для упрощения вычислений мы положили в (10.10) 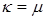 .
.
Теперь, зная собственные значения матрицы, можно определить и соответствующие им собственные вектора. Для того чтобы определить первый собственный вектор, надо в уравнение (10.13) подставить вместо  найденное
найденное 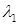 и найти ненулевой вектор, являющийся решением этой системы:
и найти ненулевой вектор, являющийся решением этой системы:
|
|
|
 (10.17)
(10.17)
Здесь следует сделать два замечания:
1. Найденный в (10.17) вектор  не единственное возможное решение. Нетрудно убедиться, что решением системы (10.17) является любой вектор, кратный найденному
не единственное возможное решение. Нетрудно убедиться, что решением системы (10.17) является любой вектор, кратный найденному  , например,
, например,  и, вообще, любой вектор вида
и, вообще, любой вектор вида  , где
, где  – произвольное число, не равное нулю. Таким образом, правильнее было бы говорить о собственном направлении, а не о собственном векторе. Но мы, естественно, следуем установившейся в литературе терминологии.
– произвольное число, не равное нулю. Таким образом, правильнее было бы говорить о собственном направлении, а не о собственном векторе. Но мы, естественно, следуем установившейся в литературе терминологии.
2. Вообще говоря, собственным вектором матрицы  называется такой вектор
называется такой вектор  , который после умножения на эту матрицу не меняет своего направления
, который после умножения на эту матрицу не меняет своего направления 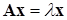 . Очевидно, этому определению удовлетворяют все вектора, о которых шла речь в первом замечании. Однако на практике удобно из этого бесконечного множества одинаково направленных векторов выбирать один по какому-то одному правилу. Есть разные варианты для выбора такого правила, однако чаще всего принято выбирать вектор с единичной длиной. Так, вектор, найденный в (10.17), согласно этому правилу следует разделить на его длину
. Очевидно, этому определению удовлетворяют все вектора, о которых шла речь в первом замечании. Однако на практике удобно из этого бесконечного множества одинаково направленных векторов выбирать один по какому-то одному правилу. Есть разные варианты для выбора такого правила, однако чаще всего принято выбирать вектор с единичной длиной. Так, вектор, найденный в (10.17), согласно этому правилу следует разделить на его длину  . Нормированный собственный вектор, соответствующий первому собственному значению, следовательно, будет
. Нормированный собственный вектор, соответствующий первому собственному значению, следовательно, будет
 . (10.18)
. (10.18)
Здесь, кстати, мы первый раз применили обычное обозначение для собственного вектора, которого будем придерживаться и в дальнейшем: чтобы отличать собственный вектор от произвольного вектора 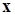 , собственный вектор обозначается строчной буквой с индексом. Индекс указывает, какому собственному значению соответствует данный собственный вектор.
, собственный вектор обозначается строчной буквой с индексом. Индекс указывает, какому собственному значению соответствует данный собственный вектор.
Теперь, совершенно аналогично, определяем второй собственный вектор, соответствующий собственному значению 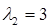 :
:
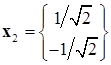 . (10.19)
. (10.19)
Итак, решение задачи о собственных значениях получено. Осталось разобраться в его физическом смысле. Вспомним, что мы пришли к задаче о собственных значениях (10.12)
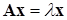
после того как для поиска решения системы дифференциальных уравнений (10.9)

использовали представление (10.11)
 .
.
При этом для упрощения выкладок было введено обозначение  .
.
 |
Определив таким образом
 и
и 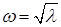 , тем самым мы определили, как изменяется вектор обобщенных перемещений системы. Заменяя математические термины терминами механики, можно сказать, что если на механическую систему не действуют внешние силы, то эта система либо покоится (
, тем самым мы определили, как изменяется вектор обобщенных перемещений системы. Заменяя математические термины терминами механики, можно сказать, что если на механическую систему не действуют внешние силы, то эта система либо покоится ( – тривиальное решение системы (10.12)), либо совершает периодические колебания с частотой
– тривиальное решение системы (10.12)), либо совершает периодические колебания с частотой  по форме, определяемой вектором
по форме, определяемой вектором  . Это высказывание поясняет рис. 10.2, на котором пунктирной линией обозначены положения равновесия грузов. Первая форма колебаний представляет собой смещение грузов в одном направлении, при колебаниях по второй форме грузы движутся в противоположных направлениях (как иногда говорят – в противофазе). Какая из форм колебаний реализуется в действительности, зависит от начальных условий. Если, например, отвести грузы на одно расстояние в одну сторону и отпустить, то реализуется первая форма колебаний, если грузы развести в разные стороны – вторая. В действительности чистых колебаний только по одной форме почти никогда не встречается. Обычно форма колебаний механической системы представляет собой комбинацию собственных форм. Известно, например, что своеобразие звучания струнных музыкальных инструментов обусловлено именно возникновением кроме основных колебаний струны с низшим тоном и колебаний с более высокой частотой – обертонов.
. Это высказывание поясняет рис. 10.2, на котором пунктирной линией обозначены положения равновесия грузов. Первая форма колебаний представляет собой смещение грузов в одном направлении, при колебаниях по второй форме грузы движутся в противоположных направлениях (как иногда говорят – в противофазе). Какая из форм колебаний реализуется в действительности, зависит от начальных условий. Если, например, отвести грузы на одно расстояние в одну сторону и отпустить, то реализуется первая форма колебаний, если грузы развести в разные стороны – вторая. В действительности чистых колебаний только по одной форме почти никогда не встречается. Обычно форма колебаний механической системы представляет собой комбинацию собственных форм. Известно, например, что своеобразие звучания струнных музыкальных инструментов обусловлено именно возникновением кроме основных колебаний струны с низшим тоном и колебаний с более высокой частотой – обертонов.|
|
|
После подробного разбора простого примера может возникнуть впечатление, что никаких сложностей в задаче о собственных значениях нет. Для ее решения, похоже, надо всего-навсего:
1) определить корни полинома  -й степени:
-й степени:
 ;
;
2) определить вектора, соответствующие полученным собственным значениям.
Увы, все не так просто. Хотя такой подход в принципе осуществим, для решения задачи о собственных значениях он крайне неэффективен. Когда приходится иметь дело с полиномами степени 5 и выше, для нахождения его корней мы не можем воспользоваться явными формулами, как в случае квадратного уравнения. Еще в начале прошлого века Галуа[1] доказал, что для нахождения корней многочлена пятой степени не существует алгебраической формулы. Поэтому для нахождения корней такого полинома приходится прибегать к численным итерационным методам. Для полиномов общего вида такие методы разработаны и хорошо исследованы (методы Берстоу, Мюллера, Лина,Лобачевского-Греффе, Бернулли и др.[10.3, 10.4]). Однако попытка использовать их для задачи (10.1) в случае матрицы с размерностью в несколько сотен даже современные компьютеры заставило бы трудиться безостановочно в течение нескольких часов.
|
|
|
К счастью 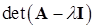 из (10.14) является довольно частным случаем полинома. Как уже отмечалось в 3-й лекции, в задачах механики, как правило, приходится иметь дело с симметричными положительно определенными матрицами. В этом случае возможно использование значительно более «быстрых» алгоритмов.
из (10.14) является довольно частным случаем полинома. Как уже отмечалось в 3-й лекции, в задачах механики, как правило, приходится иметь дело с симметричными положительно определенными матрицами. В этом случае возможно использование значительно более «быстрых» алгоритмов.
Литература
10.1. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Физматгиз, 1961. – 312с.
10.2. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1978. – 304с.
10.3. Хемминг Р.В. Численные методы для научных работников и инженеров. – М.: Наука, 1972. – 400с.
10.4. Хаусхолдер А.С. Основы численного анализа. – М.: ИЛ, 1956. – 320с.
[1] Галуа Эварист (1811-1832) – французский математик. Труды по теории алгебраических уравнений положили начало развитию современной алгебры. Научное наследие Галуа – небольшое число весьма кратко написанных работ, из-за новизны идей, не понятых при жизни Галуа. Погиб на дуэли.
|
|
|


