 |
Метод итераций в подпространстве
|
|
|
|
Лекция 14
Итерации в подпространстве
Метод итераций в подпространстве
Метод основан на уже известном нам степенном методе. Отличие заключается в том, что итерации выполняются не с одним, а несколькими векторами.
Простейшая реализация метода заключается в следующем.
1. Выбираются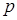 
нормированных и взаимно ортогональных векторов 
. Эти вектора удобно представить себе как столбцы матрицы 
размера 
:
. (17.1)
2. Выполняется итерация, которая в данном случае представляет собой умножение исследуемой матрицы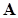 
на матрицу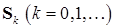 
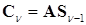. (17.2)
В этот момент проверяется сходимость. Если отношения элементов первого столбца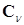 
и соответствующих элементов первого столбца 
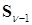одинаковы (в реальных вычислениях очень близки), то первый столбец есть собственный вектор, соответствующий наибольшему собственному значению матрицы 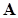. Само же это отношение и будет искомым собственным значением 
:
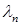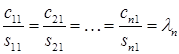. (17.3)
3. Столбцы полученной матрицы 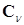ортонормируют (процесс Грама-Шмидта). Полученную матрицу размера 
обозначаем 
и ее столбцы рассматриваем как очередное приближение собственных векторов. Этот шаг является важным дополнением по сравнению со степенным методом. Если бы его не было, все столбцы стремились бы к одному и тому же собственному вектору 
.
4. Переход ко второму шагу алгоритма и продолжение итераций до достижения сходимости.
Алгоритм итераций в подпространстве используется, когда надо определить несколько собственных значений и соответствующих векторов. Если требуется определить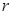 
собственных пар, то, с целью ускорения сходимости, для итераций используется несколько большее число векторов. Например, неплохим выбором количества итерационных векторов будет 
. Следует иметь в виду, что увеличение количества 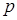итерационных векторов (иными словами, увеличение размерности подпространства) повышает скорость сходимости, но при этом каждая итерация будет требовать большего количества вычислений.
|
|
|
Пример. Для матрицы
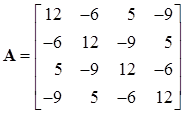
по методу итераций в подпространстве определить два наибольших собственных значения и соответствующие собственные векторы. Для справки, точное решение задачи:
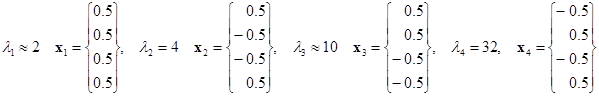
В качестве начальных векторов берем два единичных орта:
.
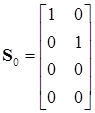Первая итерация:
.
Вторая итерация:
.
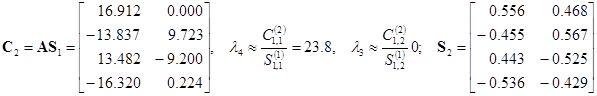Третья итерация:
.
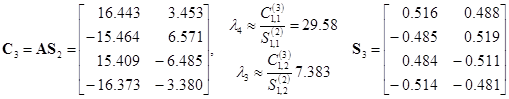Четвертая итерация:
.
Как видим, процесс движется в должном направлении. Правда, сходимость довольно медленная. Если продолжить вычисления, то точность в три значащие цифры после запятой будет достигнута после одиннадцатой итерации.
Использование процедуры Рэлея ‑ Ритца позволяет значительно усовершенствовать алгоритм. При этом описание алгоритма несколько усложняется, Но скорость сходимости итерационного процесса значительно повышается
1. Как и в предыдущем варианте, сначала формируется система начальных векторов, которые удобно представить в виде столбцов прямоугольной матрицы:
(17.4)
Эти векторы размерности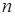 
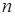( ‑ размер исследуемой матрицы 
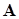) должны быть нормированы и ортогональны между собой. В остальном их выбор произволен. Количество итерируемых векторов 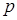(количество столбцов в матрице ) определяется исполнителем расчетов.
2. Выполняется умножение матрицы итерируемых векторов на исследуемую матрицу:
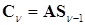(17.5)
Полученная матрица 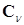имеет тот же размер (количество строк и столбцов), что и матрица 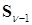, но столбцы ее уже не будут ортонормированны между собой.
3. Столбцы полученной матрицы 
ортонормируют с использованием процедуры Грама-Шмидта. Полученную матрицу размера обозначим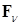 
.
4. В соответствии с процедурой Релея-Ритца формируется матрица
|
|
|
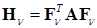(17.6)
5. Для полученной матрицы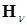 
размера 
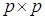решается полная проблема собственных значений:
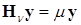(17.7)
Результатом решения (17.7) будут собственные значения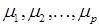 
и соответствующие собственные векторы 
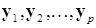. Из этих векторов формируем матрицу:
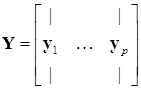(17.8)
6. Матрица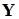 
дает возможность построить матрицу ортонормированных итерационных векторов очередного приближения
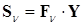(17.9)
В этот момент можно проверить, достигнута ли необходимая точность, или итерации следует продолжить. Для продолжения итераций следует вновь перейти к пункту 2 данного плана. Проверку сходимости можно выполнить путем сравнения матриц и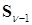
Пример. Рассматриваем ту же задачу, что и в предыдущем примере с тем же выбором начальных векторов:
,
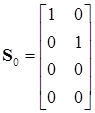Первая итерация:
; 
.
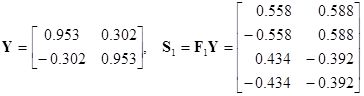Вторая итерация:
; 
.
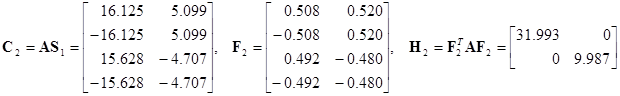Третья итерация:
; 
.
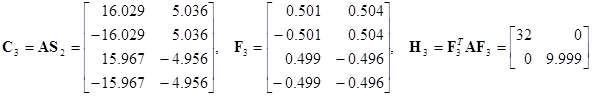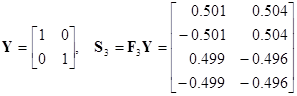Четвертая итерация:
; 
.
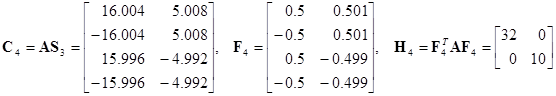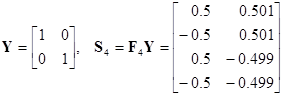Как видим, использование процедуры Рэлея ‑ Ритца значительно повышает скорость сходимости метода.
Литература
17.1. Парлетт Б. Симметричная проблема собственных значений. Численные методы. – М.: Мир, 1983. – 384с.
|
|
|
