 |
Краткие сведения о решении систем нелинейных уравнений
|
|
|
|
Лекция 9
Нелинейные системы
Краткие сведения о решении систем нелинейных уравнений
Системы нелинейных уравнений могут возникать при интегрировании уравнений движения деформируемых систем, при решении задач оптимизации и во многих других случаях. Наиболее часто количество уравнений в таких системах количество уравнений равно количеству неизвестных. Во всяком случае, это справедливо для большинства задач вычислительной механики.
Общий вид таких систем:
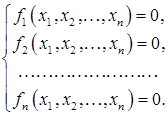 (9.1)
(9.1)
Как обычно запись системы (9.1) можно значительно упростить, введя векторные обозначения. Обозначим 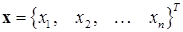 ‑ вектор, содержащий неизвестные, а
‑ вектор, содержащий неизвестные, а 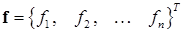 ‑ вектор функций.
‑ вектор функций.
Система (9.1) принимает вид
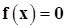 , (9.2)
, (9.2)
внешне совпадающий с единственным уравнением с одним неизвестным, методы решения которого были рассмотрены в предыдущих параграфах. Однако обобщение этих методов на многомерный случай представляет существенные трудности.
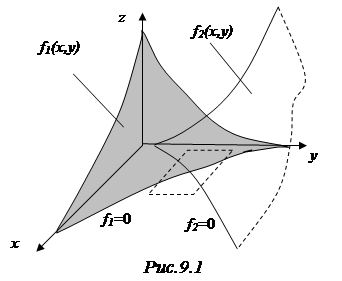 Начнем, как обычно, с графической иллюстрации (Рис.9.1). Рассмотрим систему двух уравнений с двумя неизвестными:
Начнем, как обычно, с графической иллюстрации (Рис.9.1). Рассмотрим систему двух уравнений с двумя неизвестными:
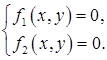
На рисунке изображены две поверхности, определяемые уравнениями 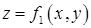 и
и 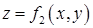 . Очевидно, что уравнения
. Очевидно, что уравнения 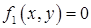 и
и 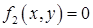 представляют собой уравнения линий пересечения этих поверхностей с плоскостью
представляют собой уравнения линий пересечения этих поверхностей с плоскостью 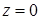 . Соответственно точка пересечения этих линий и определяет решение исходной системы.
. Соответственно точка пересечения этих линий и определяет решение исходной системы.
Попытка обобщить эти наглядные представления на системы с большим количеством уравнений, пожалуй, мало полезна. Хотя в некоторых книгах по численным методам (например, [9.1]) можно встретить формулировку типа: Решение представляет собой точку 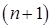 -мерного пространства, в которой
-мерного пространства, в которой 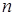 гиперповерхностей
гиперповерхностей  пересекаются с гиперплоскостью
пересекаются с гиперплоскостью 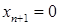 . Звучит красиво, но, на мой взгляд, наглядностью не отличается.
. Звучит красиво, но, на мой взгляд, наглядностью не отличается.
|
|
|
Уже на двумерном случае понятно, что метод половинного деления здесь, к сожалению, не работает. Для одного уравнения этот метод, не отличаясь высокой скоростью, был с другой стороны крайне надежным. Но для одного уравнения в методе бисекций на каждом шаге требовалось вычислить значения функций на границах интервала, то есть всего в двух точках. Уже для двух уравнений аналогичный подход требует определения значений функций на границе двумерной области (пунктирный прямоугольник на рисунке), то есть в бесконечном числе точек.
 Более плодотворной выглядит попытка применить идею метода касательных. На рис.9.2 изображены поверхности
Более плодотворной выглядит попытка применить идею метода касательных. На рис.9.2 изображены поверхности 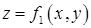 и
и 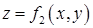 . И на этом рисунке видно, что эти две поверхности и плоскость
. И на этом рисунке видно, что эти две поверхности и плоскость 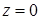 пересекаются в точке, координаты которой и представляют решение системы
пересекаются в точке, координаты которой и представляют решение системы
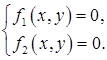
В качестве начального приближения мы принимаем некоторую точку 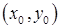 , изображенную на рисунке кружком. На первой поверхности этим значениям аргументов соответствует точка, отмеченная на рисунке крестиком, с координатами
, изображенную на рисунке кружком. На первой поверхности этим значениям аргументов соответствует точка, отмеченная на рисунке крестиком, с координатами 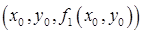 . На второй поверхности – точка с координатами
. На второй поверхности – точка с координатами 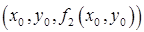 . Проведем через точку
. Проведем через точку 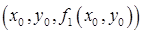 плоскость касательную к поверхности
плоскость касательную к поверхности 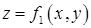 . На рисунке фрагмент этой плоскости изображен темным треугольником, ограниченным пунктирной линией. Через точку
. На рисунке фрагмент этой плоскости изображен темным треугольником, ограниченным пунктирной линией. Через точку 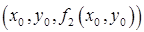 проводим плоскость касательную к поверхности
проводим плоскость касательную к поверхности 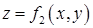 . На рисунке эта плоскость изображена треугольником, ограниченным линиями из точек. Точка
. На рисунке эта плоскость изображена треугольником, ограниченным линиями из точек. Точка 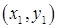 , в которой эти плоскости пересекаются между собой и с плоскостью
, в которой эти плоскости пересекаются между собой и с плоскостью 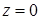 , принимается в качестве очередного приближения. И далее эта процедура повторяется до тех пор, пока не будет достигнута необходимая точность.
, принимается в качестве очередного приближения. И далее эта процедура повторяется до тех пор, пока не будет достигнута необходимая точность.
Теперь попробуем перевести эти довольно приблизительные рассуждения перевести на язык формул. Для случая 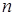 уравнений с
уравнений с 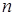 неизвестными начальное приближение определяется вектором:
неизвестными начальное приближение определяется вектором:

Очередное приближение можно представить как
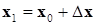 , или
, или 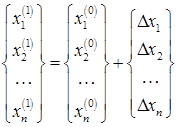
|
|
|
Если разложить функции 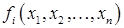 , определяющие систему (9.1) в ряд Тейлора в окрестности точки
, определяющие систему (9.1) в ряд Тейлора в окрестности точки 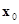 (см, например [9.2]), получим следующие выражения:
(см, например [9.2]), получим следующие выражения:
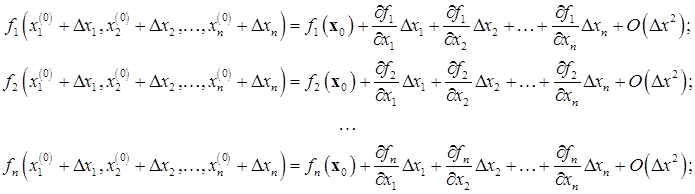 (9.3)
(9.3)
Производные здесь вычисляются, разумеется, в точке 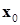 . В методе Ньютона-Рафсона (методе касательных) при определении очередного приближения мы заменяем функции
. В методе Ньютона-Рафсона (методе касательных) при определении очередного приближения мы заменяем функции 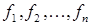 (криволинейные поверхности) их линейными приближениями (касательными плоскостями), то есть в выражениях (9.3) отбрасываем члены второго порядка малости
(криволинейные поверхности) их линейными приближениями (касательными плоскостями), то есть в выражениях (9.3) отбрасываем члены второго порядка малости  . Полагая значения функций в левой части уравнений (9.3) равными нулю, приходим к системе уравнений
. Полагая значения функций в левой части уравнений (9.3) равными нулю, приходим к системе уравнений
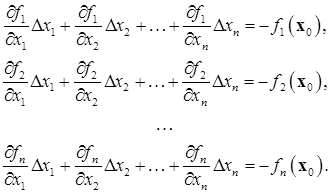
В матричной записи эта система выглядит таким образом:
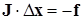 , (9.4)
, (9.4)
где
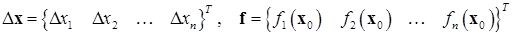 ,
,
а матрица 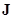
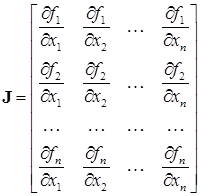 (9.5)
(9.5)
представляет собой хорошо известный по курсу матанализа якобиан.
В случае если якобиан не вырожден 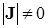 , система уравнений (9.4) имеет единственное решение:
, система уравнений (9.4) имеет единственное решение: 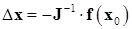 , и очередное приближение решения имеет вид:
, и очередное приближение решения имеет вид: 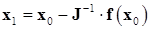 . Таким образом, итерационная формула метода Ньютона-Рафсона для системы линейных уравнений имеет вид:
. Таким образом, итерационная формула метода Ньютона-Рафсона для системы линейных уравнений имеет вид:
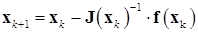 (9.6)
(9.6)
Если рассматривать якобиан как обобщение производной, то можно сказать, что формулы этого метода для системы уравнений и для одного уравнения совпадают.
При программной реализации обычно не вычисляют матрицу обратную якобиану непосредственно, а сначала вычисляют поправку, решая систему
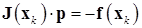 , (9.7)
, (9.7)
и затем определяют очередное приближение:
 . (9.8)
. (9.8)
Объем вычислений для систем, естественно, значительно больше, чем для одного уравнения и, к сожалению, не всегда сходится к решению. В программном комплексе MATLAB для решения систем уравнений можно использовать функцию fsolve (содержится в Optimization Toolbox). Если вы поэкспериментируете с этой функцией, то обнаружите, что не так уж редко функция будет сообщать либо о том, что сходимости добиться не удалось, либо о том, что процесс сходится к некоторой точке, но эта точка не является нулем функций системы.
Вообще проблема решения систем нелинейных уравнений вида еще далека от своего окончательного решения. Не случайно, поэтому, хорошие программы предусматривают возможность неудачи и сообщают о ее причинах.
Что касается метода Ньютона-Рафсона, определяемого формулой (9.6), то он, обладает квадратичной сходимостью, превосходя по эффективности другие методы. Однако для его успешной работы необходимо выполнение следующих условий:
|
|
|
· Якобиан должен быть достаточно хорошо обусловленной матрицей. Иначе будет затруднительно вычислить поправку 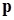 с хорошей точностью.
с хорошей точностью.
· Начальное приближение 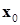 должно быть достаточно хорошим. Иначе первая же поправка, определяемая по формуле (9.7) может дать не приближение к решению, а удаление от него.
должно быть достаточно хорошим. Иначе первая же поправка, определяемая по формуле (9.7) может дать не приближение к решению, а удаление от него.
В формулировке обоих этих условий присутствует слово достаточно, не отличающееся здесь математической точностью. И действительно, чаще всего, определить ‑ достаточно ли хорошо выбрано начальное приближение можно только предприняв попытку решения.
Поэтому, как правило, метод Ньютона-Рафсона используют в комбинации с другими методами и применяя различные меры предосторожности. Здесь приведем, предложенную в книге [9.3] стратегию решения ‑ относительно простую, но достаточно надежную. Она основана на ограничении величины поправки 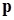 (уравнения (9.7) и (9.8)) и требовании уменьшения величин функций
(уравнения (9.7) и (9.8)) и требовании уменьшения величин функций  с каждой поправкой.
с каждой поправкой.
1) Вводится ограничение на величину поправки 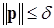 , где
, где 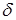 ‑ заданный допуск.
‑ заданный допуск.
2) Если 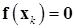 ‑ останов.
‑ останов.
3) Вычислить 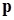 . Здесь используется не формула (9.7)
. Здесь используется не формула (9.7) 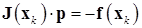 , но решается задача оптимизации (минимизации): определить
, но решается задача оптимизации (минимизации): определить 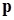 , обеспечивающее минимум функции
, обеспечивающее минимум функции 
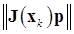 при условии
при условии 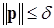 . (Здесь должны использоваться специальные методы оптимизации, не рассматриваемые в данном курсе. Ознакомиться с ними можно по упомянутой книге Каханера, Моулера, Нэша)
. (Здесь должны использоваться специальные методы оптимизации, не рассматриваемые в данном курсе. Ознакомиться с ними можно по упомянутой книге Каханера, Моулера, Нэша)
4) Если 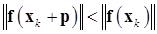 , то шаг принимается как удачный, полагается
, то шаг принимается как удачный, полагается 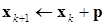 и
и 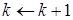 . Управление возвращается на второй шаг алгоритма.
. Управление возвращается на второй шаг алгоритма.
5) Иначе полагаем 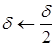 . Управление передается на третий шаг алгоритма
. Управление передается на третий шаг алгоритма
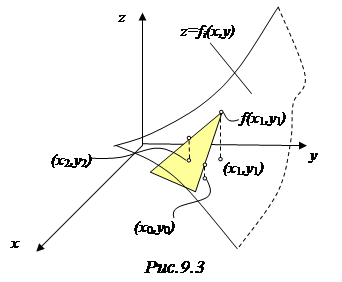
Возможно также обобщение метода секущих на многомерный случай. На рис.9.3 приведена соответствующая иллюстрация для системы двух уравнений. В этом случае для первого приближения надо выбрать три начальных точки 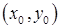 ,
, 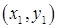 ,
,  . На каждой из поверхностей
. На каждой из поверхностей 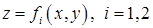 (на рисунке показана только одна из этих поверхностей) этим точкам соответствуют три точки 3-х мерного пространства:
(на рисунке показана только одна из этих поверхностей) этим точкам соответствуют три точки 3-х мерного пространства: 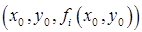 ,
, 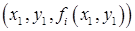 ,
, 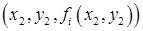 . Через эти три точки можно провести секущую плоскость. На рисунке эта плоскость изображена затемненным треугольником. Пересечение двух таких плоскостей с плоскостью
. Через эти три точки можно провести секущую плоскость. На рисунке эта плоскость изображена затемненным треугольником. Пересечение двух таких плоскостей с плоскостью 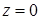 дает точку
дает точку  , которая считается новым приближением. Для следующей итерации одна из ранее выбранных точек 0,1,2 заменяется на новую 3-ю точку.
, которая считается новым приближением. Для следующей итерации одна из ранее выбранных точек 0,1,2 заменяется на новую 3-ю точку.
|
|
|
 В случае системы
В случае системы 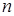 уравнений для проведения гиперплоскости в
уравнений для проведения гиперплоскости в 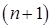 -мерном пространстве требуется задать
-мерном пространстве требуется задать 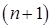 точку. В остальном последовательность действий остается такой же.
точку. В остальном последовательность действий остается такой же.
Существует много разновидностей метода секущих, использующий различные способы выбора точек и различные стратегии решения. Ознакомиться с ними можно по книге Ортеги, Рейнболдта [9.1]. Здесь же отметим только, что метод секущих и в многомерном случае можно рассматривать как вариант метода Ньютона-Рафсона с заменой производных их приближенными выражениями через значения функций в отдельных точках (разностными соотношениями).
Вопрос о сходимости методов здесь рассмотрим на примере метода простой итерации. Так же как и в случае одной функции можно ввести понятия неподвижной точки и сжимающего отображения
Рассмотрим некоторую 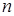 -мерную вектор-функцию
-мерную вектор-функцию 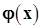 от
от 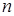 переменных. Здесь
переменных. Здесь 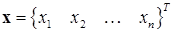 . Эту функцию можно рассматривать как оператор, отображающий точки
. Эту функцию можно рассматривать как оператор, отображающий точки 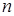 -мерного пространства на то же самое пространство.
-мерного пространства на то же самое пространство.
Определение 1. Точка  для которой
для которой  называется неподвижной точкой оператора (функции)
называется неподвижной точкой оператора (функции) 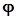 .
.
Определение 2. Оператор (функция) 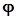 называется сжимающим оператором на некотором множестве
называется сжимающим оператором на некотором множестве 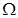 , если для любых значений
, если для любых значений 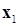 и
и 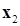 , принадлежащих этому множеству
, принадлежащих этому множеству 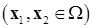 , выполняется неравенство
, выполняется неравенство
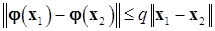 , (9.9)
, (9.9)
где 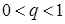 называется коэффициентом сжатия.
называется коэффициентом сжатия.
Для исследования сходимости итерационных методов принципиальное значение имеет следующая теорема:
Принцип сжимающих отображений. Пусть оператор 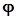 определен на множестве
определен на множестве 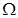 , представляющем собой окрестность некоторой точки
, представляющем собой окрестность некоторой точки 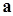 :
: 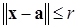 и является на этом множестве сжимающим оператором с коэффициентом сжатия
и является на этом множестве сжимающим оператором с коэффициентом сжатия 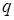 , причем
, причем
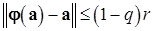 .
.
Тогда итерационный метод 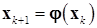 сходится к неподвижной точке оператора
сходится к неподвижной точке оператора 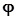 при любом начальном приближении
при любом начальном приближении 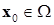 .
.
Доказательства этой теоремы здесь не приводится. Более подробную информацию по этому вопросу можно найти в книгах [9.1, 9.4].
Отметим, что, как и в случае одного уравнения, вместо условия (9.9) можно, с некоторыми оговорками, воспользоваться более строгим условием:
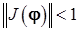 для
для 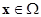 (9.10)
(9.10)
(норма якобиана функции 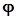 меньше единицы).
меньше единицы).
Сформулированный выше принцип сжимающих отображений применим для исследования сходимости только таких итерационных методов, которые являются разновидностями метода простой итерации. То есть метода, который исходную систему уравнений
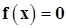
заменяет эквивалентной системой вида
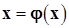
и определяет итерационную последовательность как
|
|
|
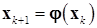
Метод Ньютона-Рафсона удовлетворяет этому описанию, если положить  . Метод секущих, в котором для получения очередного приближения используются уже не одна, а несколько точек, уже не является методом простой итерации. И исследование сходимости здесь представляет большие сложности.
. Метод секущих, в котором для получения очередного приближения используются уже не одна, а несколько точек, уже не является методом простой итерации. И исследование сходимости здесь представляет большие сложности.
Литература
9.1. Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. – М.: Мир, 1975. – 558 с.
9.2. Смирнов В.И. Курс высшей математики. Том I. – М.: Наука, 1967. – 480 с.
9.3. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение. – М.: Мир, 1998. – 575 с.
9.4. Самарский А.А., Гулин А.В. Численные методы. ‑ М.: Наука, 1989. – 432 с.
|
|
|


