 |
Метод наискорейшего спуска
|
|
|
|
Лекция 5. Метод сопряженных градиентов
Метод сопряженных градиентов
Метод, рассматриваемый в настоящем параграфе, предназначен для решения систем 
в случае, когда матрица 
является симметричной и положительно определенной. В этом он подобен методу Холецкого. Но в этом методе не требуется выполнять операции с полной матрицей 
. Достаточно иметь возможность для любого вектора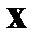 
получать вектор 
.
Рассмотрим следующую функцию:
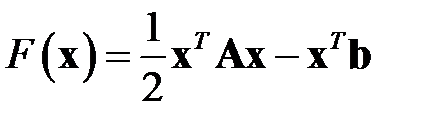(5.1)
Несложно убедиться, что условием минимума этой функции является выполнение системы линейных уравнений:
(5.2)
Таким образом, решение СЛАУ (5.1) и отыскание минимума функции (5.1) являются эквивалентными задачами.
Градиент функции (5.1):
(5.4)
Напомним, что градиент функции – это вектор, имеющий направление, в котором функция возрастает с наибольшей скоростью.
Отсюда следует, что если мы имеем какое-то очередное приближение вектора неизвестных 
, то следующее приближение 
логично искать в направлении, противоположном направлению градиента:
(5.5)
Введем обозначение:
(5.6)
Тогда (5.5) принимает простой вид:
(5.7)
Вектор 
называют вектором невязок системы 
. Смысл названия следующий. Если бы 
являлся решением этой системы, то, как видно из (5.6) вектор невязок был бы тождественно равен нулю. Таким образом, наличие ненулевых элементов в 
говорит о том, что 
не является решением системы . Геометрический смысл вектора невязки – направление, в котором функция (5.1) убывает быстрее всего. Или, как иногда говорят, направление наискорейшего спуска.
Остается определить, каким следует принять число 
. То есть, на какое расстояние следует переместиться от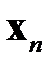 
в направлении 
, чтобы получить наилучшее возможное приближение для очередного приближения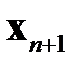 
?
|
|
|
Этот вопрос решается просто. Подставим в функцию (5.1) выражение для очередного приближения (5.7):
(5.8)
Поскольку 
‑ это фиксированный вектор предыдущего приближения, выражение (5.8) представляет собой функцию одной переменной 
. А условие минимума такой функции:
позволяет получить выражение для 
:
(5.9)
Это значение 
гарантирует, что для очередного приближения 
значение функции (5.1) будет меньше, чем для предыдущего. Заметим, что при получении формулы (5.9) использовался тот факт, что матрица 
является симметричной.
На основании этих выкладок можно сформулировать следующий итерационный алгоритм решения системы (или, что то же самое, минимизации функции (5.1)):
Метод наискорейшего спуска
1. Выбирается вектор начального приближения 
.
2. Для 
выполняются следующие вычисления
,
, (5.10)
3. Останавливать итерационный процесс следует, когда норма очередного вектора невязки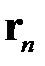 
окажется меньше заданной малой величины.
Обратите внимание на то, что для проведения вычислений не нужна вся матрица 
целиком. Достаточно иметь возможность для любого вектора получить произведение матрицы на этот вектор. Эта особенность алгоритма особенно важна для больших разреженных матриц.
Этот алгоритм выгладит очень простым. Но должен огорчить читателя. Это еще не конец параграфа. Сформулированный метод – это еще не метод сопряженных градиентов. И этот метод – метод наискорейшего спуска – обладает существенным недостатком.
Для систем с плохо обусловленной матрицей, когда собственные значения матрицы 
значительно различаются по величине, этот метод может сходиться очень медленно.
Причины этого можно наглядно объяснить следующим образом. Для таких задач линии уровня функции (5.1) представляют собой сильно вытянутые замкнутые линии (см рис.5.1). Как показано на этом рисунке, возникает ситуация, когда направление наискорейшего спуска направлено не к точке минимума функции (5.1), а почти перпендикулярно к желаемому направлению. Графически итерационный процесс в этом случае можно представить в виде ломаной из коротких отрезков. Каждый отрезок лишь незначительно приближает к искомому решению.
|
|
|
Рис.5.1
Метод сопряженных градиентов является усовершенствованием рассмотренного метода наискорейшего спуска.
Пусть очередное приближение решения системы (5.2): 
. Очередное приближение теперь ищется в виде:
(5.11)
Здесь вектор 
, который называется «вектором направления» и определяется следующим образом.
(5.12)
где 
‑ вектор направления предыдущей итерации.
Число 
определяется из условия А-сопряженности вектора направления 
к вектору 
. Под А-сопряженностью этих векторов понимается соотношение:
(5.13)
Несложные выкладки позволяют получить из (5.13) выражение для 
:
(5.14)
Величина 
определяется из тех же соображений, что и в методе наискорейшего спуска. Подставляя (5.11) в функцию (5.1) получим функцию одной переменной:
(5.15)
Условие минимума этой функции:
Позволяет получить выражение для 
:
(5.16)
Итак, получены все необходимые формулы для того чтобы определить следующий итерационный метод для решения систем линейных уравнений.
|
|
|
