 |
Обобщенная симметричная задача собственных значений
|
|
|
|
Лекция 13
Обобщенная проблема и процедура Релея Ритца
Обобщенная симметричная задача собственных значений
В рассмотренных выше примерах механическая система специально подбиралась таким образом, что матрица масс системы была диагональной. В этом случае (см. лекцию 10) уравнения колебаний (уравнения Лагранжа 2-го рода) приводятся к задаче
 (15.1)
(15.1)
 с симметричной матрицей
с симметричной матрицей  .
.
Однако рассмотрим следующий пример (рис. 15.1), отличающийся от примера из 10-й лекции лишь тем, что:
1) второй груз тяжелее первого в два раза;
2) пружины не считаются невесомыми, но имеют массу  .
.
 В этом случае вновь потенциальная энергия системы складывается из потенциальных энергий деформации пружин:
В этом случае вновь потенциальная энергия системы складывается из потенциальных энергий деформации пружин:
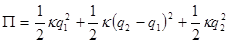 . (15.2)
. (15.2)
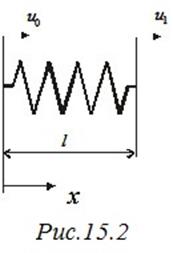
Что касается кинетической энергии системы, то сначала получим выражение для кинетической энергии отдельной пружины (рис. 15.2). Продольные перемещения в продольном направлении изменяются по линейному закону:
 (15.3)
(15.3)
Тогда, обозначив  массу пружины, получим для кинетической энергии пружины следующее выражение:
массу пружины, получим для кинетической энергии пружины следующее выражение:
 . (15.4)
. (15.4)
Теперь, имея формулу (15.4), мы можем без труда записать выражение для кинетической энергии всей системы (рис. 15.1), которая складывается из кинетических энергий двух грузов и трех пружин:
 . (15.5)
. (15.5)
Вновь, как в лекции 10, воспользуемся уравнениями Лагранжа 2-го рода:
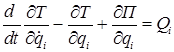 . (15.6)
. (15.6)
После вычисления производных кинетической и потенциальной энергий (15.5), (15.2) и подстановки их в (15.6) получим уравнения колебаний системы:
 (15.7)
(15.7)
или в матричном виде
 , (15.8)
, (15.8)
где
 . (15.9)
. (15.9)
Теперь стандартная подстановка  приводит (15.7) к виду
приводит (15.7) к виду
 . (15.10)
. (15.10)
Казалось бы, умножив (15.10) на  , это уравнение можно привести к виду (15.1):
, это уравнение можно привести к виду (15.1):
 . (15.11)
. (15.11)
Однако хотя и матрица жесткости  , и матрица инерции
, и матрица инерции  симметричны, матрица
симметричны, матрица  оказывается симметричной лишь в частных случаях. Таких, например, как приведенные в лекции 10 где матрица
оказывается симметричной лишь в частных случаях. Таких, например, как приведенные в лекции 10 где матрица  была диагональной. Для рассмотренной выше задачи, которая совсем ненамного сложней, получим, положив для определенности
была диагональной. Для рассмотренной выше задачи, которая совсем ненамного сложней, получим, положив для определенности  ,
,
|
|
|
 . (15.12)
. (15.12)
Что же это получается? Почти все рассмотренные методы были предназначены для симметричных матриц. И вот оказывается, что в большинстве случаев, представляющих практический интерес, эти методы неприменимы.
Конечно это не так, иначе мы не стали бы тратить столько времени на их изучение. Задача
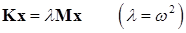 (15.13)
(15.13)
в случае симметричных матриц  и
и  сводится к задаче
сводится к задаче
 (15.14)
(15.14)
с симметричной матрицей 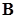 следующим образом.
следующим образом.
Сначала выполним разложение матрицы  по схеме Холецкого:
по схеме Холецкого:
 . (15.15)
. (15.15)
Это разложение возможно, так как матрица масс механической системы по физическому смыслу является положительно определенной. Подставляя (15.15) в (15.13) и вводя обозначение
 , (15.16)
, (15.16)
приводим систему (15.13) к виду
 (15.17)
(15.17)
где  .
.
Матрица 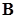 симметрична, так как
симметрична, так как
 . (15.18)
. (15.18)
Подводим итог. Собственные значения так называемой обобщенной задачи на собственные значения (15.13) при симметричных матрицах  и
и  совпадают с собственными значениями симметричной задачи (15.14), где матрица
совпадают с собственными значениями симметричной задачи (15.14), где матрица 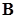 определяется через
определяется через  и
и  (15.17). При этом собственные вектора обобщенной задачи
(15.17). При этом собственные вектора обобщенной задачи  выражаются через собственные вектора симметричной задачи соотношением (15.16).
выражаются через собственные вектора симметричной задачи соотношением (15.16).
Заключительное замечание. В преобразовании (15.17) используется матрица, обратная к треугольной 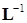 . Сложно ли получить матрицу обратную данной? Нет, не сложно, и особенно для треугольной матрицы. В самом деле, если ввести обозначение
. Сложно ли получить матрицу обратную данной? Нет, не сложно, и особенно для треугольной матрицы. В самом деле, если ввести обозначение  , то, согласно определению обратной матрицы,
, то, согласно определению обратной матрицы,
 (15.19)
(15.19)
Из определения матричного произведения следует, что (15.19) можно рассматривать как 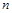 линейных систем вида:
линейных систем вида:
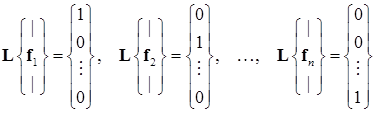 , (15.20)
, (15.20)
где  – столбцы матрицы
– столбцы матрицы  .
.
Поскольку матрица  - треугольная, системы (15.20) решаются очень легко. Кстати, с точки зрения эффективности алгоритма нет необходимости решать одну за другой
- треугольная, системы (15.20) решаются очень легко. Кстати, с точки зрения эффективности алгоритма нет необходимости решать одну за другой  систем (15.20). Гораздо меньше времени потребуется, если рассматривать (15.20) как одну систему, но с
систем (15.20). Гораздо меньше времени потребуется, если рассматривать (15.20) как одну систему, но с  правыми частями.
правыми частями.
|
|
|
Между прочим, в предыдущем замечании был почти полностью описан алгоритм вычисления обратной матрица, известный как метод Гаусса ‑ Жордана [1]. Для обращения произвольной невырожденной матрицы  по этому методу следует сначала сформировать матрицу размера
по этому методу следует сначала сформировать матрицу размера  и занести в первые
и занести в первые  столбцов матрицу
столбцов матрицу  , а в оставшиеся
, а в оставшиеся  столбцов – единичную матрицу порядка
столбцов – единичную матрицу порядка  :
:
 . (15.21)
. (15.21)
Далее к матрице применяется метод Гаусса. При этом сам процесс исключения выполняется только один раз, а операции с правыми частями повторяются для каждого столбца правой половины матрицы (15.21). Решение системы для каждого варианта правых частей заносится на место соответствующего столбца ‑ вектора правой части. Тогда по окончании процедуры Гаусса правые  столбцов (15.21) будут содержать
столбцов (15.21) будут содержать  решений системы вида:
решений системы вида:
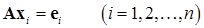 , (15.22)
, (15.22)
где через  обозначен
обозначен  -й столбец единичной матрицы.
-й столбец единичной матрицы.
Очевидно, что эти  столбцов и будут содержать матрицу обратную
столбцов и будут содержать матрицу обратную  , так как согласно (15.22)
, так как согласно (15.22)
 . (15.23)
. (15.23)
§ 16. Задачи большой размерности. Процедура Рэлея [2] -Ритца
До сих пор мы не задумывались над такими вопросами:
1. Хватит ли памяти компьютера, чтобы разместить в ней исследуемую матрицу?
2. Не окажется ли время, необходимое для решения задачи, чрезмерно большим?
Современная вычислительная техника обеспечивает пользователя такими ресурсами, что эти вопросы могут показаться излишними. Они действительно не возникают, пока размерность задачи
 (16.1)
(16.1)
не превышает нескольких сотен. Однако для сегодняшней вычислительной практики характерны задачи с размерностью  степеней свободы. К таким задачам относятся расчеты силовых конструкций самолета, ракеты, колебаний сопла ракетного двигателя, надежности ядерных реакторов, задачи аэро- и гидродинамики…[13.1].
степеней свободы. К таким задачам относятся расчеты силовых конструкций самолета, ракеты, колебаний сопла ракетного двигателя, надежности ядерных реакторов, задачи аэро- и гидродинамики…[13.1].
Если модель конструкции содержит  степеней свободы, то матрица жесткости будет состоять из
степеней свободы, то матрица жесткости будет состоять из  чисел. Объем памяти, необходимый для запоминания такой матрицы,
чисел. Объем памяти, необходимый для запоминания такой матрицы,  . Столько же памяти потребуется для собственных векторов. Кроме того, эти матрицы должны не просто запоминаться, но и активно использоваться в последовательных приближениях. Рассмотренные метод Якоби и QR-алгоритм не в состоянии решать задачи таких размеров за более-менее приемлемое время.
. Столько же памяти потребуется для собственных векторов. Кроме того, эти матрицы должны не просто запоминаться, но и активно использоваться в последовательных приближениях. Рассмотренные метод Якоби и QR-алгоритм не в состоянии решать задачи таких размеров за более-менее приемлемое время.
|
|
|
Однако задачи большой размерности имеют особенности, которые все-таки позволяют их решать, несмотря на ограниченность ресурсов и быстродействия современной вычислительной техники.
Во-первых, такие задачи возникают, как правило, при описании процессов, конструкций, явлений и т.п. с помощью либо МКЭ (метода конечных элементов), либо МКР (метода конечных разностей). Матрицы, получаемые при использовании этих методов, практически всегда сильно разрежены. Это значит, что при большой размерности самой матрицы большинство ее элементов равны нулю. Такие матрицы обычно не заносятся в память целиком, а запоминаются в компактной форме, без нулевых элементов. Возникает ситуация, когда нам надо решать задачу о собственных значениях  , не имея в своем распоряжении матрицу
, не имея в своем распоряжении матрицу  в явном виде, но имея лишь правило, позволяющее для произвольного вектора
в явном виде, но имея лишь правило, позволяющее для произвольного вектора  получать произведение
получать произведение  .Это, с одной стороны, полезно, так как позволяет уместить задачу в памяти компьютера. С другой стороны, алгоритм решения такой задачи не должен испытывать неудобств из-за того, что исследуемая матрица
.Это, с одной стороны, полезно, так как позволяет уместить задачу в памяти компьютера. С другой стороны, алгоритм решения такой задачи не должен испытывать неудобств из-за того, что исследуемая матрица  в явном виде недоступна.
в явном виде недоступна.
Во-вторых, обычно при решении таких задач важны не все собственные значения, а лишь значения, лежащие в определенной части спектра. Так, при расчете собственных колебаний конструкции планера самолета обычно практический интерес представляют лишь несколько низших частот.
Прежде чем перейти к рассмотрению методов для решения больших задач, необходимо рассмотреть алгоритм Рэлея ‑ Ритца, являющийся необходимой составной частью таких методов. В названии этого алгоритма соединились два имени, которые упоминаются преподавателями сопротивления материалов, теории упругости едва ли не чаще чем имена основателей этих научных дисциплин Коши, Ламе, Сен-Венана… Между тем оба этих ученых непосредственно не занимались вопросами механики деформируемых твердых тел.
|
|
|
Английский барон Джон Уильям Рейли (Rayleigh) является одним из основоположников теории звука (акустики) и теории колебаний. Его знаменитая теорема (1873 г.) гласит, что «при увеличении жесткости системы или уменьшении ее инерции главные частоты увеличиваются» [13.2]. Принцип Релея, который следует из его теоремы: отношение Рэлея
 (16.2)
(16.2)
минимально, если  равно первому собственному вектору и равно в этом случае наименьшему собственному значению
равно первому собственному вектору и равно в этом случае наименьшему собственному значению 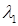 :
:
 . (16.3)
. (16.3)
Этот принцип часто используется для грубой оценки минимальной частоты механической системы. Для совершенно произвольного вектора 
 . (16.4)
. (16.4)
В простых случаях примерный вид низшей формы колебаний можно предугадать исходя из физического смысла задачи. Так, для консольной балки хорошим приближением выглядит квадратичная парабола, для колеблющейся струны – полуволна синусоиды.
Немецкий математик Ритц, опубликовав в 1909 г. статью о новом методе решения вариационных задач математической физики [13.3], возможно не подозревал, что к концу XX века его идеи, воплотившись в конце концов в методе конечных элементов, практически вытеснят из практики другие способы решения задач прочности, аэродинамики, теплопроводности и т.д.
Метод Ритца предназначен для решения вариационной задачи:
Среди всех функций  , определенных и непрерывных в интервале
, определенных и непрерывных в интервале  , имеющих непрерывные первую и вторую производные и удовлетворяющие краевым условиям
, имеющих непрерывные первую и вторую производные и удовлетворяющие краевым условиям  и
и  , найти такую, для которой
, найти такую, для которой
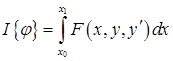 (16.5)
(16.5)
имеет наименьшее (или наибольшее) возможное значение.
В случае, если аналитическое решение задачи (16.5) невозможно или затруднительно, метод Ритца служит универсальной палочкой-выручалочкой:
1. Задаемся системой линейно-независимых функций
 , (16.6)
, (16.6)
удовлетворяющих граничным условиям:
 (16.7)
(16.7)
2. Предполагаем, что неизвестное решение задачи (16.5) можно представить в виде линейной комбинации
 . (16.8)
. (16.8)
3. Подстановка (8) в (5) превращает вариационную задачу в обычную задачу математического анализа об экстремуме функции многих переменных:
 (16.9)
(16.9)
4. В результате все дело сводится к нахождению  неизвестных коэффициентов
неизвестных коэффициентов  из системы
из системы  уравнений:
уравнений:
 (16.10)
(16.10)
Метод Ритца легко обобщается на двумерные  и трехмерные
и трехмерные  задачи.
задачи.
Хотя метод Ритца задуман для нахождения непрерывной функции  , его можно применить и для решения нашей задачи о собственных значениях матрицы
, его можно применить и для решения нашей задачи о собственных значениях матрицы  .
.
Алгоритм Рэлея-Ритца для задачи о собственных значениях:
1. Задаемся ортонормированной системой векторов:
 . (16.11)
. (16.11)
2. Предполагаем, что искомый собственный вектор можно представить в виде линейной комбинации векторов  :
:
 , (16.12)
, (16.12)
где
 . (16.13)
. (16.13)
3. Подставляя (16.12) в (16.1), получаем
|
|
|
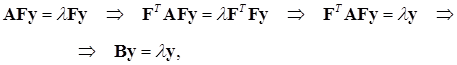 (16.14)
(16.14)
здесь введено обозначение  , а
, а  , так как матрица
, так как матрица  имеет ортонормированные столбцы.
имеет ортонормированные столбцы.
4. Решая задачу  , находим пары собственных значений и собственных векторов:
, находим пары собственных значений и собственных векторов:
 . (16.15)
. (16.15)
5. Аналогично решению вариационной задачи полагаем, что приближенное решение полной задачи (16.1) можно получить из решения сокращенной задачи (16.14)
 (16.16)
(16.16)
Здесь сразу следует оговориться, что хотя этот алгоритм является важной составной частью методов Ланцоша и метода итераций в подпространстве, однако сам по себе метод Рэлея – Ритца использовать для решения задачи о собственных значениях нельзя. Точность результатов полностью зависит от того, насколько нам повезет с выбором векторов  .
.
Пример. Для матрицы
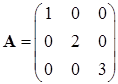 (16.17)
(16.17)
точное решение задачи  , очевидно, есть
, очевидно, есть
 (16.18)
(16.18)
Что получится, если применить процедуру Рэлея ‑ Ритца для поиска 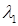 и
и 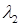 ?
?
Сначала выбираем в качестве ортонормированной системы векторов
 . (16.19)
. (16.19)
Тогда матрица 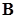 сокращенной задачи (16.14):
сокращенной задачи (16.14):
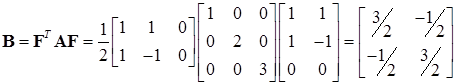 (16.20)
(16.20)
имеет собственные значения  .
.
Затем выберем следующую ортонормированную систему:
 (16.21)
(16.21)
и для сокращенной матрицы 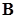
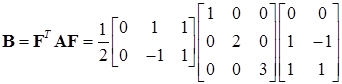 (16.22)
(16.22)
получим собственные значения  .
.
Как видим, в первом случае выбор векторов  и
и  оказался удачным. Причина этого в том, что первый собственный вектор матрицы
оказался удачным. Причина этого в том, что первый собственный вектор матрицы  лежит в плоскости, определенной векторами
лежит в плоскости, определенной векторами  и
и  . В результате
. В результате  точно совпало с первым собственным значением исследуемой матрицы. Во втором случае, напротив, вектора
точно совпало с первым собственным значением исследуемой матрицы. Во втором случае, напротив, вектора  и
и  были выбраны настолько неудачно, насколько это вообще возможно. Первый собственный вектор исследуемой матрицы
были выбраны настолько неудачно, насколько это вообще возможно. Первый собственный вектор исследуемой матрицы  не то что не лежит в плоскости векторов
не то что не лежит в плоскости векторов  и
и  , но даже ортогонален к ней.
, но даже ортогонален к ней.
Тем не менее, как бы ни был неудачен выбор векторов  в алгоритме Рэлея ‑ Ритца, всегда можно быть уверенным, что
в алгоритме Рэлея ‑ Ритца, всегда можно быть уверенным, что
1)  ;
;
2) если какой-нибудь собственный вектор исходной матрицы  точно представляется в виде линейной комбинации
точно представляется в виде линейной комбинации  , то в результате решения сокращенной задачи этот собственный вектор и соответствующее собственное значение будут найдены точно.
, то в результате решения сокращенной задачи этот собственный вектор и соответствующее собственное значение будут найдены точно.
Можно сказать, что процедура Релея-Ритца исходную задачу  , определенную для
, определенную для  -мерного алгебраического пространства, заменяет на задачу, представляющую собой, в некотором смысле, проекцию исходной задачи на
-мерного алгебраического пространства, заменяет на задачу, представляющую собой, в некотором смысле, проекцию исходной задачи на  -мерное подпространство (
-мерное подпространство ( ).
).
Литература
13.1. Данилин А.Н., Солдаткин А.Н. Вычислительные методы динамики упругих конструкций. – М.: Изд-во МАИ, 1996. ‑ 44с.
13.2. Рэлей Дж. В. Теория звука. Т.1 – М.: Наука, 1955. – 503с.
13.3. Ritz, W., 1909. „Über eine neue Method zur Lösung Gewisser Variationsprobleme der Mathematischen Physik.“ J. Rein. Angew. Math., 135:1-61.
[1] Жордан Камиль (1838-1922) – французский математик. Труды по алгебре, теории функций, топологии и кристаллографии.
[2] Рэлей (Рейли, Rayleigh) Джон Уильям, барон (1842-1919) – английский физик, один из основоположников теории колебаний. Фундаментальные труды по акустике, молекулярному рассеянию света. Нобелевский лауреат 1909 г.
|
|
|


