 |
Методы решения систем линейных уравнений
|
|
|
|
Лекция №3
Системы линейных уравнений. Метод Крамера, матричный способ, метод Гаусса
Системой линейных уравнений, содержащих m уравнений и п неизвестных, называется система вида
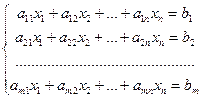
Числа 
называются коэффициентами системы; 
- свободными членами; 
- неизвестные.
Матрицей системы называется матрица, составленная из коэффициентов при неизвестных
Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов:
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет множество решений.В этом случае каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Две системы называются эквивалентными, если они имеют одно и то же общее решение. Эквивалентные системы получаются при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками системы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю. Однородная система всегда совместна, так как 
является решением системы. Это решение называется нулевым решением.
Решить систему уравнений – значит выяснить, совместна она или несовместна, если совместна – найти её общее решение.
Исчерпывающий ответ на вопрос о совместности системы линейных уравнений дает теорема Кронекера – Капелли.
Для того, чтобы система m линейных уравнений относительно n неизвестных была совместна (имела решение), необходимо и достаточно, чтобы ранг основной матрицы системы А был равен рангу расширенной матрицы системы В: т.е. r (A) = r (B)
|
|
|
Если r (A) = r (B) = n (числу неизвестных), то система имеет единственное решение.
Если r (A) = r (B) < n, то система имеет множество решений.
Методы решения систем линейных уравнений
Пусть дана система n линейных уравнений с n неизвестными:
.
Решение системы такого вида можно найти по методу Крамера, матричным способом, методом Гаусса.
1.Метод Крамера.
Если определитель системы отличен от нуля, то система имеет единственное решение, которое определяется по формулам:
,…., 
,
где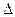 
- главный определитель системы, а 
(i=1,2,…,n) – определитель, полученный из главного определителя системы заменой i-того столбца столбцом свободных членов.
Если определитель системы 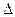= 0, а хотя бы один из определителей 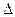I отличен от нуля, то система не имеет решения.
Если определитель системы 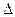= 0, и все 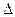I = 0, то система имеет множество решений.
Пример. Решить систему уравнений
Решение. Вычислим определител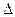и и 
:
Используя формулы Крамера, находим решение системы:
.
2.Матричный метод.
Введем обозначения: матрицу системы обозначим через А, матрицу-столбец неизвестных через Х, матрицу-столбец свободных членов через В
, 
, 
.
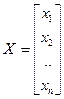Тогда систему линейных уравнений можно записать в виде:
.
Для решения этого матричного уравнения умножим обе части равенства слева на А-1:
Так как 
, то 
Откуда решение системы – матрица-столбец неизвестных находится по формуле:
, где А-1 – обратная матрица к матрице А.
Пример. Решить систему линейных уравнений матричным методом: 
.
Решение. Имеем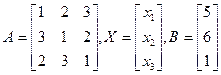 
.
Находим обратную матрицу к матрице А по формуле 
.
Определитель матрицы равен: detA = 18, присоединенная матрица равна: 
. Тогда обратная матрица будет равна:
.
Теперь находим матрицу Х по формуле 
, получим:
= 
.
Т.е. х1 = 1, х2 = -1, х3 = 2.
|
|
|
3. Метод Гаусса.
Это метод последовательного исключения неизвестных. Он заключается в том, что с помощью элементарных преобразований система линейных уравнений приводится к треугольному виду. Решая полученную систему уравнений с конца, находим все неизвестные.
Пример. Решить систему уравнений методом Гаусса:
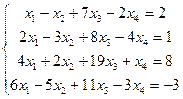
Решение. Для удобства преобразования будем выполнять не над уравнениями, а над матрицами, составленными из коэффициентов при неизвестных и свободных членов.
Составим матрицу из коэффициентов и свободных членов, и приведем ее к треугольному виду:
~ 
~ 
~ 
По полученной матрице составляем систему уравнений:
Начиная с последнего уравнения находим все неизвестные:
х3 = 0, х4 = -2, х2 = 3, х1 =1. Т.е. решение системы имеет вид:(1,3,0,-2).
Пример. Решить систему уравнений: 
.
Решение. Составим матрицу из коэффициентов при неизвестных и свободных членов, и приведем ее к треугольному виду.
~ 
~ 
Составляем систему: 
. Из последнего уравнения выразим переменную х2 через х3: х2 = 
и подставим в первое уравнение. Откуда находим переменную х1: х1 = 
. Т. е. решение системы примет вид: 
. Придавая переменной х3 различные числовые значения, получим множество решений системы.
Контрольные вопросы к лекции №3
1. Какая система называется совместной? Несовместной? Определенной? Неопределенной?
2. Сформулировать теорему Кронекера-Капелли.
3. В чем заключается метод Крамера?
4. Решение систем линейных уравнений матричным методом.
5. Метод Гаусса.
|
|
|
