 |
Сделайте выводы о соответствии выбранной парной линейной модели регрессии эмпирическим данным - по всем показателям адекватности и качества модели.
|
|
|
|
Лабораторная работа №1. Парная линейная регрессия
Цель работы
Построение парной линейной регрессии и проверка значимости.
Проверка статистической значимость значений коэффициентов регрессии и коэффициента корреляции.
Вычисление доверительных интервалов параметров линейной регрессии.
Построение прогноза и вычисление стандартных ошибок прогноза
Содержаниеотчета и представление работы
Отчет по работе оформляется в виде файла Excel и должен содержать полученные результаты с необходимыми пояснениями.
Задание к работе
Исходные данные смоделированы на основе линейной эконометрической модели:
 ,
,
где случайные величины  взаимно независимы и нормально распределены с нулевым математическим ожиданием и дисперсией
взаимно независимы и нормально распределены с нулевым математическим ожиданием и дисперсией  .
.
Исходные данные представляют собой двумерную выборку

По выборке необходимо построить парную линейную регрессию и проверить ее статистическую значимость.
1. Для заданных исходных данных постройте поле корреляции — диаграмму зависимости показателя  от фактора
от фактора  : тип диаграммы «Точечная» (без отрезков, соединяющих точки).
: тип диаграммы «Точечная» (без отрезков, соединяющих точки).

Рис. 1. Диаграмма зависимости показателя  от фактора
от фактора  .
.
2. Найдите выборочные характеристики  ,
, 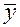 ,
,  ,
,  ,
,  ,
,  ,
,  , используя средства Excel, результаты вычислений оформить в виде таблицы (рис. 2.):
, используя средства Excel, результаты вычислений оформить в виде таблицы (рис. 2.):
— выборочные средние значения  и
и 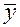 , функция AVERAGE/ СРЗНАЧ.
, функция AVERAGE/ СРЗНАЧ.
Вычисления в Excel реализованы по формулам  ,
,  ;
;
— смещенные выборочные оценки дисперсии  и
и  , функция VARP/ ДИСПР.
, функция VARP/ ДИСПР.
В Excel реализованы формулы  ,
,  .
.
— смещенные выборочные средние квадратические отклонения  и
и  , STDEVP/ СТАНДОТКЛОНП. Вычисления в Excel выполнены по формулам
, STDEVP/ СТАНДОТКЛОНП. Вычисления в Excel выполнены по формулам
 ,
,  .
.
— выборочный коэффициент корреляции  , функция CORREL/ КОРРЕЛ. В Excel реализуется формула:
, функция CORREL/ КОРРЕЛ. В Excel реализуется формула: 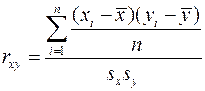 .
.
|
|
|

Рис. 2. Выборочные характеристики, вычисленные средствами Excel.
 3. Найдите коэффициенты a и b выборочной линейной регрессии, используя средства Excel
3. Найдите коэффициенты a и b выборочной линейной регрессии, используя средства Excel 
Для вычисления коэффициентов воспользуйтесь встроенной функцией LINEST/ ЛИНЕЙН (функция находится в категории “Статистические” и вычисляет выборочные оценки  и
и 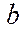 параметров
параметров  уравнения регрессии
уравнения регрессии  ):
):
1) В свободном месте рабочего листа выделите область ячеек размером 5 строк и 2 столбца для вывода результатов.
2) В Мастере функций (категория “Статистические”) выберите функцию LINEST /ЛИНЕЙН.
3) Заполните поля аргументов функции:
Известные_значения_y — адреса ячеек, содержащих значения признака  ;
;
Известные_значения_x — адреса ячеек, содержащих значения фактора  ;
;
Константа — логическое значение, указывающее на наличие свободного члена a в уравнении регрессии: укажите значение поля Константа равное 1, тогда свободный член рассчитывается обычным образом (если значение поля Константа равно 0, то свободный член полагается равным 0);
Статистика — логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет: укажите значение поля Статистика равное 1, тогда выводится дополнительная регрессионная информациям (если Статистика = 0, то выводятся только оценки параметров уравнения регрессии — оценки a и b).
4) После того, как будут заполнены все аргументы функции, нажмите комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.
Расчеты параметров регрессионной модели выводятся в виде таблицы:
Таблица 1.
Значение коэффициента 
| Значение коэффициента 
|
Стандартная ошибка  коэффициента
коэффициента 
| Стандартная ошибка  коэффициента
коэффициента 
|
Коэффициент детерминации 
| Оценка стандартного отклонения
остатков 
|
 -статистика -статистика
| Число степеней свободы, равное 
|
Регрессионная сумма квадратов 
| Остаточная сумма квадратов 
|
|
|
|

 |





 -статистика Число степеней свободы
-статистика Число степеней свободы
Регрессионная сумма квадратов Остаточная сумма квадратов


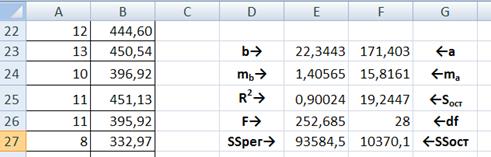
Рис. 3. Таблица результатов использования функции LINEST /ЛИНЕЙН.

4. Проверьте значения коэффициентов  ,
,  непосредственным вычислением по формулам:
непосредственным вычислением по формулам:


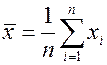 ,
,  ,
,  ,
, 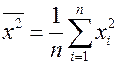

Рис. 4. Таблица значений коэффициентов  ,
,  , полученных непосредственным вычислением по формулам.
, полученных непосредственным вычислением по формулам.

5. Вычислите значения  по уравнению эмпирической регрессии:
по уравнению эмпирической регрессии:
 .
.
 6. Постройте на корреляционном поле прямую линию выборочной линейной регрессии по точкам
6. Постройте на корреляционном поле прямую линию выборочной линейной регрессии по точкам  .
.

Рис. 5. Результаты выполнения пунктов 5 и 6.

7. Вычислите остатки  .
.

8. Постройте график остатков (тип диаграммы — «Точечная»).

Рис. 5. График остатков  .
.
 9. Найдите величину средней ошибки аппроксимации
9. Найдите величину средней ошибки аппроксимации  :
:
 .
.

10. Вычислите коэффициент детерминации  непосредственно по формуле:
непосредственно по формуле:
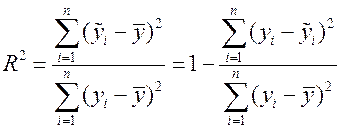
Сравните полученное значение коэффициента детерминации с вычисленным ранее с помощью функции CORREL/ КОРЕЛЛ выборочным коэффициентом корреляции.

11. Рассчитайте оценку  , стандартные ошибки параметров линейной регрессии
, стандартные ошибки параметров линейной регрессии  ,
,  и коэффициента корреляции
и коэффициента корреляции  непосредственно по формулам.
непосредственно по формулам.
 – несмещенная оценка дисперсии
– несмещенная оценка дисперсии  возмущений
возмущений 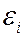 (теоретической остаточной дисперсии);
(теоретической остаточной дисперсии);
 – стандартная ошибка коэффициента регрессии
– стандартная ошибка коэффициента регрессии  ;
;
 – смещенные выборочное среднее квадратическое отклонения
– смещенные выборочное среднее квадратическое отклонения  ;
;
 – стандартная ошибка коэффициента регрессии
– стандартная ошибка коэффициента регрессии  ;
;
 – выборочный коэффициент корреляции;
– выборочный коэффициент корреляции;
 – смещенное выборочное среднее квадратическое отклонения
– смещенное выборочное среднее квадратическое отклонения  .
.
 12. Вычислите соответствующие значения
12. Вычислите соответствующие значения  – статистик для коэффициентов регрессии
– статистик для коэффициентов регрессии  ,
,  и коэффициента корреляции
и коэффициента корреляции  . Проверьте статистическую значимость полученных значений коэффициентов регрессии и коэффициента корреляции.
. Проверьте статистическую значимость полученных значений коэффициентов регрессии и коэффициента корреляции.
Статистика 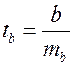 при выполнении гипотезы
при выполнении гипотезы  распределена по закону Стьюдента с n - 2 степенями свободы.
распределена по закону Стьюдента с n - 2 степенями свободы.
Из таблицы распределения Стьюдента с n - 2 степенями свободы по заданному уровню значимости выбирается значение 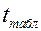 как критическая точка, соответствующая двусторонней области.
как критическая точка, соответствующая двусторонней области.
|
|
|
Тогда:
1) Если  , то гипотезу
, то гипотезу  следует отклонить и, следовательно, признать коэффициент b статистически значимым,
следует отклонить и, следовательно, признать коэффициент b статистически значимым,
2) Если  , то гипотезу
, то гипотезу  следует принять и, следовательно, признать коэффициент b статистически незначимым.
следует принять и, следовательно, признать коэффициент b статистически незначимым.
Статистика  при выполнении гипотезы
при выполнении гипотезы  распределена по закону Стьюдента с n - 2 степенями свободы.
распределена по закону Стьюдента с n - 2 степенями свободы.
Из таблицы распределения Стьюдента с n - 2 степенями свободы по заданному уровню значимости выбирается значение 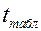 как критическая точка, соответствующая двусторонней области.
как критическая точка, соответствующая двусторонней области.
Тогда:
1) Если  , то гипотезу
, то гипотезу  следует отклонить и, следовательно, признать коэффициент a статистически значимым,
следует отклонить и, следовательно, признать коэффициент a статистически значимым,
2) Если  , то гипотезу
, то гипотезу  следует принять и, следовательно, признать коэффициент a статистически незначимым.
следует принять и, следовательно, признать коэффициент a статистически незначимым.
Статистика  при выполнении гипотезы
при выполнении гипотезы  (т.е. при отсутствии корреляционной связи, здесь
(т.е. при отсутствии корреляционной связи, здесь 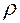 — генеральный коэффициент корреляции) распределена по закону Стьюдента с n - 2 степенями свободы.
— генеральный коэффициент корреляции) распределена по закону Стьюдента с n - 2 степенями свободы.
Из таблицы распределения Стьюдента с n - 2 степенями свободы по заданному уровню значимости 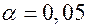 выбирается значение
выбирается значение 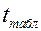 как критическая точка, соответствующая двусторонней области.
как критическая точка, соответствующая двусторонней области.
Тогда:
1) Если  , то гипотезу
, то гипотезу  следует отклонить и, следовательно, признать коэффициент
следует отклонить и, следовательно, признать коэффициент  статистически значимым,
статистически значимым,
2) Если  , то гипотезу
, то гипотезу  следует принять и, следовательно, признать коэффициент
следует принять и, следовательно, признать коэффициент  статистически незначимым.
статистически незначимым.
Проверка значимости коэффициента b одновременно является проверкой значимости парной линейной регрессии в целом. Еще один способ проверки значимости парной линейной регрессии основан на коэффициенте детерминации R2 и статистике, распределенной по закону Фишера с числом степеней свободы числителя равном 1 и числом степеней свободы знаменателя равном n - 2.
Табличные значения 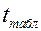 определяются с помощью функции TINV/СТЬЮДРАСПОБР. – вычисляет верхнее критическое значение
определяются с помощью функции TINV/СТЬЮДРАСПОБР. – вычисляет верхнее критическое значение  распределения Стьюдента с
распределения Стьюдента с  степенями свободы, соответствующее заданному уровню значимости
степенями свободы, соответствующее заданному уровню значимости  .
.
Аргументы этой функции:
Вероятность — уровень значимости  , можно принять равным 0,05 (т.е. 5%);
, можно принять равным 0,05 (т.е. 5%);
Степени_свободы — число степеней свободы, для парной линейной регрессии равно  , где
, где 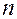 — число наблюдений.
— число наблюдений.
|
|
|

13. Проверьте значимость полученного уравнения регрессии в целом по критерию Фишера.
Если выполнены предположения регрессионного анализа, то при выполнении гипотезы  (что означает отсутствие взаимосвязи между x и y, а так же статистическую незначимость построенной парной регрессии) статистика
(что означает отсутствие взаимосвязи между x и y, а так же статистическую незначимость построенной парной регрессии) статистика  распределена по закону Фишера с числом степеней свободы числителя равном 1 и числом степеней свободы знаменателя равном n - 2.
распределена по закону Фишера с числом степеней свободы числителя равном 1 и числом степеней свободы знаменателя равном n - 2.
По таблице распределения Фишера-Снедекора при заданном уровне значимости определяется значение  как критическая точка
как критическая точка
при числе степеней свободы числителя равном 1 и числе степеней
свободы знаменателя равном n - 2.
Тогда:
1) Если  , то гипотезу
, то гипотезу  следует отклонить и, следовательно, признать построенное уравнение линейной регрессии статистически значимым,
следует отклонить и, следовательно, признать построенное уравнение линейной регрессии статистически значимым,
2) Если  , то гипотезу
, то гипотезу  следует принять и, следовательно, признать построенное уравнение статистически незначимым.
следует принять и, следовательно, признать построенное уравнение статистически незначимым.
Значение  можно определить с помощью функции FINV /FРАСПОБР. Аргументы этой функции:
можно определить с помощью функции FINV /FРАСПОБР. Аргументы этой функции:
Вероятность — уровень значимости  , можно принять равным 0,05 (т.е. 5%);
, можно принять равным 0,05 (т.е. 5%);
Степени_свободы1 — число степеней свободы числителя, равно 1 (т.к. один фактор);
Степени_свободы2 — число степеней свободы знаменателя, для парной регрессии равно  , где
, где  — число наблюдений.
— число наблюдений.

14. Вычислите доверительные интервалы параметров линейной регрессии.
Доверительные интервалы для параметров a и b с заданным уровнем доверия, в качестве которого на практике обычно выбирают вероятность 0,95 (соответствующую уровню значимости 0.05 или 5%).

 – стандартная ошибка коэффициента регрессии
– стандартная ошибка коэффициента регрессии  ;
;
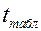 – критическое значение для заданного уровня значимости и заданного числа степеней свободы n - 2, определенное по таблицам распределения Стьюдента
– критическое значение для заданного уровня значимости и заданного числа степеней свободы n - 2, определенное по таблицам распределения Стьюдента
 ;
;
 – стандартная ошибка коэффициента регрессии
– стандартная ошибка коэффициента регрессии  .
.

15. Постройте прогноз среднего значения показателя и точечный прогноз значения  при значении
при значении  в 3 раза больше, чем среднее значение
в 3 раза больше, чем среднее значение  .
.
Точечный прогноз  значения показателя
значения показателя  согласно линейной парной регрессии для
согласно линейной парной регрессии для 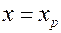 вычисляется по формуле
вычисляется по формуле

Интервальный прогноз (доверительный интервал прогноза) 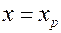 вычисляется аналогично доверительному интервалу параметров регрессии.
вычисляется аналогично доверительному интервалу параметров регрессии.
По таблицам распределения Стьюдента с n - 2 степенями свободы определяется 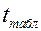 – критическое значение для заданного уровня значимости и числа степеней свободы n - 2, тогда
– критическое значение для заданного уровня значимости и числа степеней свободы n - 2, тогда

есть доверительный интервал прогноза индивидуального значения
показателя  в точке
в точке 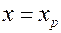 с заданным уровнем доверия
с заданным уровнем доверия
 16. Вычислите стандартные ошибки прогноза функции регрессии и индивидуального значения и доверительные интервалы полученных прогнозов.
16. Вычислите стандартные ошибки прогноза функции регрессии и индивидуального значения и доверительные интервалы полученных прогнозов.
|
|
|
Стандартная ошибка индивидуального прогноза определяется по формуле:

Очевидно, что чем дальше  от
от  , тем шире доверительный интервал прогноза, или, другими словами, тем выше погрешность прогноза.
, тем шире доверительный интервал прогноза, или, другими словами, тем выше погрешность прогноза.
 17. Получите результаты регрессионного анализа с помощью Пакета Анализ данных (Данные/Анализ данных … Регрессия | Tools/Data Analysis …Regression).
17. Получите результаты регрессионного анализа с помощью Пакета Анализ данных (Данные/Анализ данных … Регрессия | Tools/Data Analysis …Regression).
В диалоговом окне этой процедуры поля Входной интервал y, Входной интервал x, Константа имеют тот же смысл, что и для функции LINEST/ ЛИНЕЙН.
В поле Метки поставьте флажок, если первая строка в указанном диапазоне данных содержит названия столбцов.
Поставьте флажок в полях Остатки, График остатков, График подбора для того, чтобы получить соответствующую дополнительную информацию.
В результате выполнения процедуры Регрессия появляются три таблицы
- регрессионная статистика;
- дисперсионный анализ;
- таблица, содержащая коэффициенты регрессии, стандартные шибки, t - статистики и границы доверительных интервалов.

Множественный R – множественный коэффициент корреляции
 – выборочный коэффициент корреляции между фактическими
– выборочный коэффициент корреляции между фактическими  и расчетными
и расчетными  значениями зависимой переменной. В случае парной линейной регрессии этот коэффициент совпадает с выборочным коэффициентом корреляции
значениями зависимой переменной. В случае парной линейной регрессии этот коэффициент совпадает с выборочным коэффициентом корреляции 
( )
)
R-квадрат – коэффициент детерминации 
Нормированный R-квадрат – (скорректированный коэффициент детерминации)
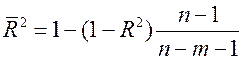
m – число факторов (для парной регрессии – один фактор, одна независимая переменная x, m = 1)
Стандартная ошибка – (выборочное стандартное отклонение остатков)

p – число параметров (для парной регрессии – параметры a и b, p = m + 1)
Наблюдения – n объем выборки.
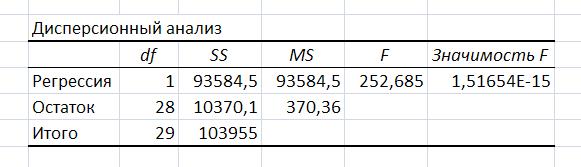
SSобщ – общая сумма квадратов отклонений  фактических значений
фактических значений  от выборочного среднего
от выборочного среднего 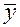 , SSобщ =103955.
, SSобщ =103955.
SSрег – сумма квадратов отклонений расчетных значений  от выборочного среднего
от выборочного среднего 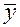 , обусловленная регрессией
, обусловленная регрессией  , SSрег = 93584,5.
, SSрег = 93584,5.
SSост – сумма квадратов остатков 
SSост = 10370,1
Эти суммы связаны равенством  , действительно 93584,5 + 10370,1 = 103955
, действительно 93584,5 + 10370,1 = 103955
MSрег – средний квадрат регрессии 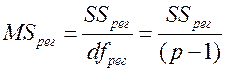
MSрег = 93584,5
MSост – средний квадрат остатков  MSост =370,36
MSост =370,36
F - статистика, служит для проверки значимость полученного уравнения регрессии в целом по критерию Фишера.
 , F = 252,685
, F = 252,685

df – число степеней свободы,
– df общ = n – 1 – число степеней свободы суммы SSобщ

– df рег = p – 1 – число степеней свободы суммы SSрег

– df ост = n – p – число степеней свободы суммы SSост

df общ = df рег + df ост
| Коэффициенты уравнения регрессии a = 171,49316b = 22,344279 | Стандартная ошибка определения коэффициентов ma = 15,81614505 mb =1,40564775 | t - статистика ta = 10,8372 tb = 15,8961 | Вероятность ошибки |







Нижние 95% – нижняя граница доверительного интервала с доверительной вероятностью 0,95, 
Верхние 95% – верхняя граница доверительного интервала с доверительной вероятностью 0,95, 
Сделайте выводы о соответствии выбранной парной линейной модели регрессии эмпирическим данным - по всем показателям адекватности и качества модели.
|
|
|


