 |
Д) Изучение экономических аспектов здравоохранения.
|
|
|
|
002. Наиболее полное определение вариационного ряда:
а) Однородная в качественном отношении статистическая совокупность, отдельные единицы которой характеризуют количественные различия изучаемого признака или явления;
б) Ряд чисел, сгруппированных в таблицу и полученных при измерении изучаемого признака у единиц наблюдения в соответствии с планом и программой исследования;
в) Количественное выражение изучаемого признака.
003. Обозначения элементов вариационного ряда:
а) V - варианта;
б) p - частота;
в) n - общее число наблюдений;
г) m - ошибка репрезентативности;
д) σ - среднее квадратическое отклонение.
004. Частота повторений варианты - это:
а) Число, указывающее, сколько раз встречается отдельная варианта в вариационном ряду, обозначаемое «p»;
б) Общее число наблюдений в вариационном ряду, обозначаемое «n»;
в) Варианта, расположенная в середине вариационного ряда, упорядоченного по возрастанию или убыванию, обозначаемая «Mе».
005. Различают следующие виды вариационных рядов:
а) Простой;
б) Ранжированный;
в) Сгруппированный;
г) Дискретный (прерывный);
д) Непрерывный;
е) Интервальный;
ж) Сложный;
з) Репрезентативный.
006. Вариационный ряд называется простым, если в нем …
а) Указано, сколько раз встречается каждая варианта;
б) Варианты расположены в порядке возрастания и указана Mо (мода);
в) Варианты расположены в порядке возрастания или убывания;
г) Каждая варианта встречается только один раз.
007. Вариационный ряд называется сгруппированным, если в нем …
а) Указано, сколько раз встречается каждая варианта;
б) Имеются варианты из двух разнородных совокупностей;
в) Имеются варианты из трех и более разнородных совокупностей;
|
|
|
г) Каждая варианта встречается только один раз.
008. Вариационный ряд называется ранжированным, если в нем …
а) Указано, сколько раз встречается каждая варианта;
б) Варианты расположены в порядке возрастания;
в) Варианты расположены в порядке убывания;
г) Каждая варианта встречается только один раз.
009. Коэффициент корреляции может изменяться в пределах (по модулю числа) …
а) От 1 до 10;
б) От 0 до 1;
в) От 0 до 100;
г) Могут встречаться любые значения.
010. Вариационный ряд называется дискретным, если в нем …
а) Указано, сколько раз встречается каждая варианта;
б) Варианты расположены в порядке возрастания;
в) Варианты представлены только целыми числами;
г) Варианты сгруппированы по величине.
011. Вариационный ряд называется непрерывным, если в нем …
а) Указано, сколько раз встречается каждая варианта;
б) Варианты расположены в порядке возрастания;
в) Варианты представлены только целыми числами;
г) Варианты представлены любыми числовыми значениями;
д) Варианты сгруппированы по величине.
012. Средняя величина – это …
а) Максимальная величина признака в вариационном ряду, характеризующая наивысший уровень явления в статистической совокупности;
б) Общая количественная характеристика изучаемого признака в вариационном ряду, вычисленная в качественно однородной статистической совокупности;
в) Общая характеристика всех признаков статистической совокупности.
013. Общими характеристиками значений вариант вариационного ряда являются:
а) Средняя арифметическая;
б) Мода;
в) Медиана;
г) Амплитуда;
д) Размах;
е) Лимит.
014. Средняя арифметическая расcчитываeтся следующими способами:
а) Простым;
б) Взвешенным;
в) Способом моментов;
г) Дискретным;
д) Непрерывным;
е) Сгруппированным.
015. Средняя арифметическая обозначается знаком:
|
|
|
а) Ϭ - сигма;
б) n малая;
в) М большая;
г) m малая;
д) r малая;
е) t малая.
016. Варианты в вариационном ряду обозначаются знаком …
а) Ϭ - сигма;
б) n;
в) М;
г) m;
д) V;
е) t.
017. Частота встречаемости варианты в вариационном ряду обозначается знаком:
а) Ϭ - сигма;
б) n;
в) М;
г) p;
д) V;
е) t.
018. Число наблюдений в вариационном ряду обозначается знаком:
а) Ϭ - сигма;
б) n;
в) М;
г) m;
д) p;
е) t.
019. Формула вычисления простой средней арифметической:
а) 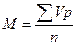 ;
;
б)  ;
;
в) 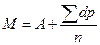 .
.
020. Формула вычисления взвешенной средней арифметической:
а) 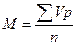 ;
;
б)  ;
;
в) 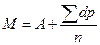 .
.
021. Формула вычисления средней арифметической по способу моментов:
а) 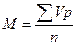 ;
;
б)  ;
;
в) 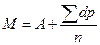 .
.
022. Основными свойствами средней арифметической величины являются…
а) Сумма всех отклонений от средней равна 0;
б) При умножении (делении) всех вариант на один и тот же множитель (делитель) средняя арифметическая умножается (делится) на тот же множитель (делитель);
в) Если прибавить (вычесть) ко всем вариантам одно и то же число, средняя арифметическая увеличивается (уменьшается) на то же число;
г) Может быть только целым числом;
д) Может быть только положительным числом.
023. Амплитуда (размах) вариант в вариационном ряду обозначается …
а) M большая;
б) m малая;
в) Аm;
г) r малая;
д) t малая;
е) Ϭ – сигма.
024. Амплитуда (размах) вариант в вариационном ряду вычисляется по формуле …
а)  ;
;
б)  ;
;
в)  .
.
025. Среднее квадратическое отклонение обозначается …
а) M;
б) m;
в) Аm;
г) r;
д) t;
е) Ϭ.
026. Среднее квадратическое отклонение характеризует…
а) Возможные отклонения параметров генеральной совокупности по сравнению с выборочной совокупностью;
б) Разницу между вариантой и средней арифметической;
в) Среднее отклонение всех вариант вариационного ряда от средней арифметической.
027. Среднее квадратическое отклонение может рассчитываться следующими способами:
а) Простым;
б) Как средневзвешенное;
в) Способом моментов;
г) Прямым;
д) Обратным.
028. Статистический критерий, которым можно сопоставить степень разнообразия вариационных рядов, если единицы измерения вариант в них различны, называется…
а) Ошибка репрезентативности;
б) Среднее квадратическое отклонение;
в) Коэффициент вариации;
|
|
|
г) Критерий Стьюдента;
д) Коэффициент корреляции.
029. Формула расчета коэффициента вариации:
а)  ;
;
б)  ;
;
в)  .
.
030. Степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации до 10%, является …
а) Малой;
б) Средней;
в) Сильной.
031. Степень рассеяния вариант вокруг средней арифметической,
если значение коэффициента вариации от 10 до 20%, является …
а) Малой;
б) Средней;
в) Сильной.
032. Степень рассеяния вариант вокруг средней арифметической, если значение коэффициента вариации более 20%, является …
а) Малой;
б) Средней;
В) Сильной.
033. «Правило трех сигм» - это…
а) Правило отбора единиц наблюдения в статистическую совокупность;
б) Вероятностная зависимость между значением средней арифметической, средним квадратическим отклонением и вариантами;
в) Отношение средней величины к среднему квадратическому отклонению.
034. Доверительный интервал – это …
а) Размах колебаний средней арифметической изучаемого признака, который можно оценить статистическими методами;
б) Разница между максимальной и минимальной вариантами;
в) Разница между средним квадратическим отклонением и ошибкой репрезентативности;
г) Отношение средней величины к среднему квадратическому отклонению.
035. Ошибка репрезентативности …
а) Является мерой изменчивости значения средней арифметической, которая может быть получена при повторных исследованиях;
б) Позволяет определить вероятность, с которой возможно перенести результаты изучения с выборочной совокупности на генеральную совокупность;
в) Служит оценкой рассеяния вариант.
036. Степень совпадения выборочной совокупности с генеральной оценивается с помощью:
а) Коэффициента корреляции;
б) Среднего квадратического отклонения;
|
|
|


