Погрешность результата измерения

 

Погрешность измерения – это алгебраическая разность между результатом измерения и истинным значением измеряемой физической величины. Обозначим погрешность Е (t). Ее выражение по определению (для детерминированной физической величины) имеет следующий вид

E (t) = Y (t) – x (t),

где Y (t) = – результат измерения как случайная функция; – математическое ожидание результата измерения; – центрированная случайная составляющая результата измерения как случайная функция, обусловленная наличием в процессе измерения случайных возмущающих факторов.

 

1.1 Исходные данные для расчета

 

Измеряемая физическая величина представляется следующей математической моделью

где С_i, 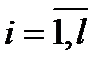- постоянные коэффициенты.

.

Математическое ожидание аддитивного возмущения, действующего на измеряемую величину, представляется также аналогичной математической моделью

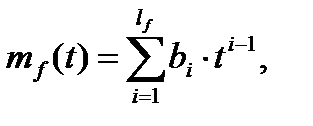
где b_i, - постоянные коэффициенты.

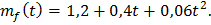
Спектральная плотность центрированной стационарной составляющей F (t) представляется следующими выражениями

1.

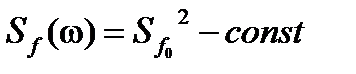
2.

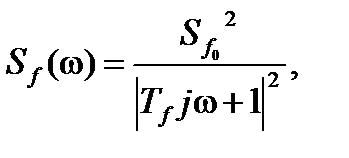
где T_f, S_{f o} – постоянные величины.

Характеристики среды оказывают двоякое влияние на результат измерения: во-первых, через искажение истинного значения измеряемой физической величины, а во-вторых, через измерение параметров, а следовательно и свойств средства измерения. Такой двоякий характер влияния среды на результат измерения послужил основанием для выделения двух основных составляющих погрешности.

 

1.2 Структурная схема формирования погрешности

 

В основу расчета характеристик погрешности результата измерения положена структурная схема формирования погрешности, приведенная на рис. 1.1.

 

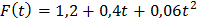
CИ

 

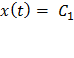
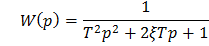
Рисунок 1. Структурная схема формирования погрешности:

x (t) – детерминированная измеряемая величина как функция времени; F (t) = m_f (t)+ F (t) – аддитивное случайное возмущение, накладывающееся на измеряемую величину; m_f(t) – математическое ожидание случайной функции F (t); F (t) = F (t) – m_f (t) – центрированная стационарная случайная функция со спектральной плотностью S_f (w); W (p) = k×W_o (p) – передаточная функция СИ; k = 1/ q = 1+D k – коэффициент чувствительности СИ; D k = – D q – отклонение коэффициента чувствительности от идеального значения, равного единице; q – размер единицы величины, воспроизводимой СИ; D q = q – 1 – погрешность единицы величины, воспроизводимой СИ; W_o (p) – нормированная передаточная функция СИ .

 

2 РАСЧЕТ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

 

Основными составляющими погрешности результата измерения, которые необходимо определить в работе являются: мультипликативная погрешность, аддитивная погрешность и суммарная погрешность. В области преобразования Лапласа выражения для этих составляющих и суммарной погрешности имеет следующий вид

уравнение суммарной погрешности;

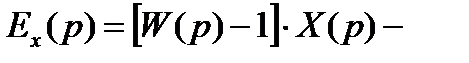уравнение мультипликативной погрешности;

уравнение аддитивной погрешности.

Используя обратное преобразование Лапласа, получим

(2.1)

(2.2)

(2.3)

где w₀(t) – нормированная весовая функция СИ,

d(t) – единичная d – функция.

Запишем выражение (2.1) в следующем виде

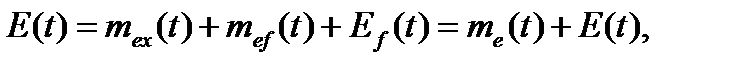(2.4)

где систематическая погрешность результата измерения,

– мультипликативная составляющая погрешности,

– аддитивная составляющая систематической погрешности (2.5),

центрированная случайная погрешность результата измерения, обусловленная случайной составляющей аддитивного возмущения, накладывающегося на измеряемую величину Х (t) на входе СИ.

 

2.1. Определение систематической погрешности результата измерения

 

Систематическая погрешность определяется на основе выражений (2.2), (2.4), (2.5) в двух режимах измерения: статическом и динамическом.

 

2.1.1 Статический режим измерения

 

Под статическим режимом измерения понимается такой режим измерения, при котором влияние инерционных свойств СИ на погрешность результата измерения пренебрежимо мало. При таком допущении можно принять и уравнения (2.2) и (2.5) записать в следующем виде

(2.7)

(2.8)

Из выражения (2.7) следует, что мультипликативная погрешность возникает из-за того, что D k = k – 1 ≠ 0, то есть из-за того, что СИ воспроизводит единицу величины не точно.

 

Пусть С ₁ = 12 В; D k =0.06; .

Решение:

На основе уравнений (2.7), (2.8) и (2.4) получим

- мультипликативная

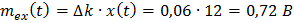
- аддитивная

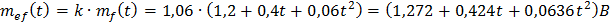
- суммарная

Графики мультипликативной, аддитивной и суммарной систематических погрешностей представлены на рисунке 2.

 

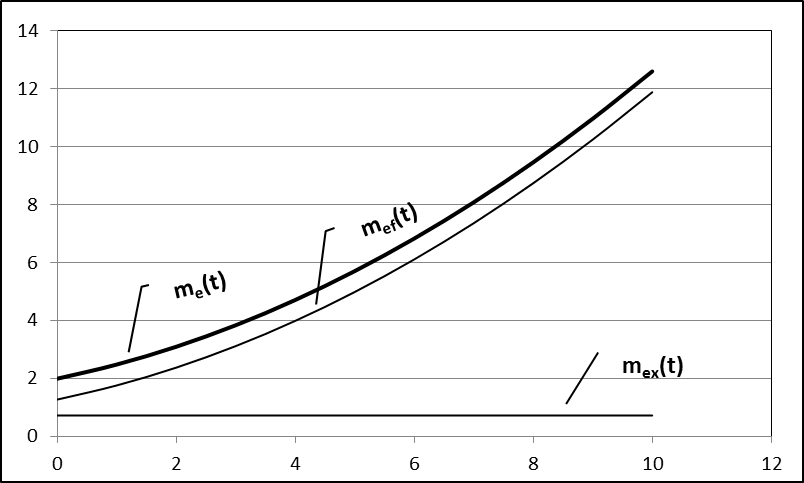
Рисунок 2. Графики мультипликативной, аддитивной и суммарной систематических погрешностей в статическом режиме

 

2.1.2. Динамический режим измерения

 

Под динамическим режимом измерения понимается такой режим измерения, при котором влиянием инерционных свойств СИ на погрешность результата измерения пренебречь нельзя. При таком допущении и, следовательно, определение мультипликативной погрешности сводится к интегрированию выражений (2.2) и (2.5).

Для случая 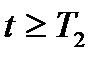(установившееся состояние СИ) и существования производных , выражения (2.2) и (2.5) могут быть представлены конечными суммами следующего вида

(2.9)

где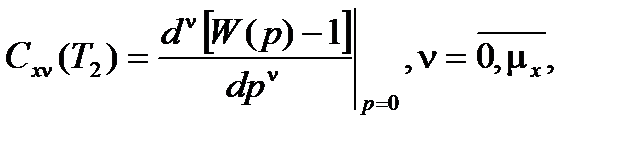

 

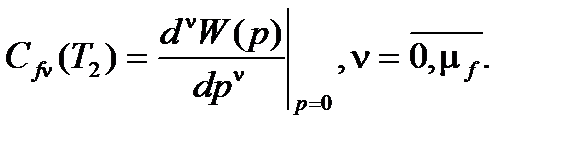
Пусть С ₁ = 12 В, D k = 0,01. Передаточная функция СИ равна

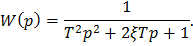
Требуется определить систематическую мультипликативную погрешность.

Решение:

Из выражения (2.9) имеем

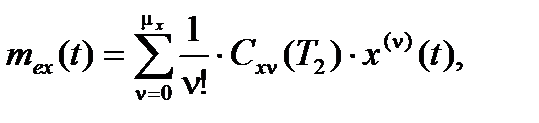
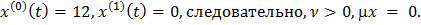
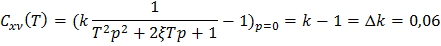
Используя полученные выражения, будем иметь

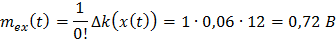
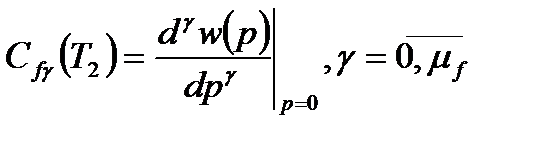
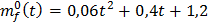
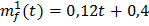
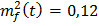
следовательно, µ=2

 

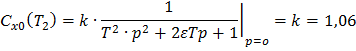
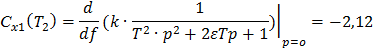
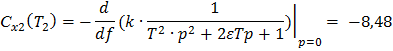
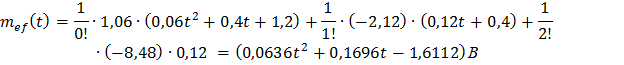
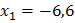
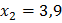
График систематической мультипликативной погрешности представлен на рисунке 3.

 

 

 

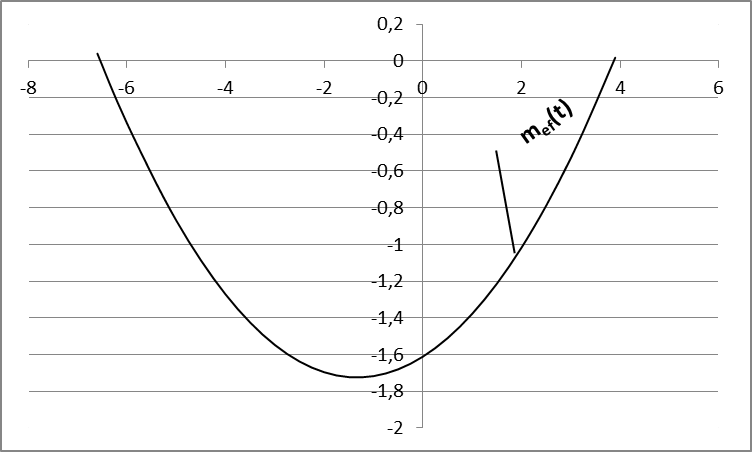
Рисунок 3. График систематической мультипликативной погрешности в динамическом режиме

 

2.2. Определение дисперсии случайной погрешности результата измерения

 

Согласно структурной схеме формирования погрешности, приведенной на рис. 1.1, центрированная случайная составляющая погрешности Е (t) обусловлена центрированным случайным возмущением F (t), характеризующимся спектральной плотностью S_f (w). Уравнения, связывающие случайные функции Е (t)и F (t), представлены выражением (2.6). Однако, это выражение не приспособлено для практического использования при определении характеристик случайной погрешности. Более предпочтительным является выражение, связывающее непосредственно спектральные плотности погрешности и случайного возмущения, а именно

(2.16)

где – спектральная плотность аддитивной погрешности Е_f (t),

– квадрат модуля частной характеристики СИ.

В свою очередь, спектральная плотность определяет такую важную числовую характеристику случайной погрешности как дисперсия. Выражение для дисперсии имеет следующий вид

.

После подстановки выражения (2.16) получим

(2.17)

В случае, если спектральная плотность S_f (w) выражается дробно-рациональной четной функцией, то интеграл

, (2.18)

где a_k, k 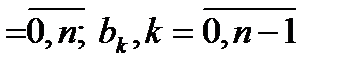- коэффициенты полиномов по j w соответственно знаменателя и числителя следующего выражения

, (2.19)

где полином степени n,

полином степени не выше 2×(n – 1).

Выражение для интегралов при n = имеют следующий вид

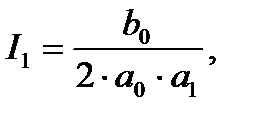
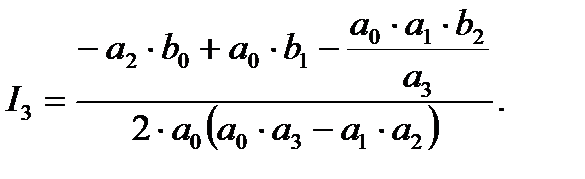
Таким образом, с учетом выражения (2.18) уравнение (2.17) запишется следующим образом

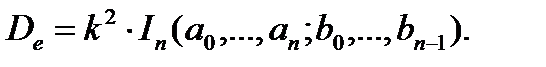(2.20)

 

Пусть k = 1,06,

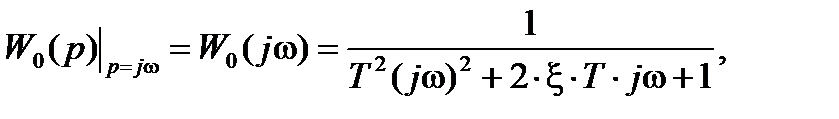
T=2 c, x = 0,7,

, ,

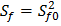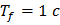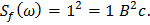
Решение:

На основе уравнения (2.18) получим

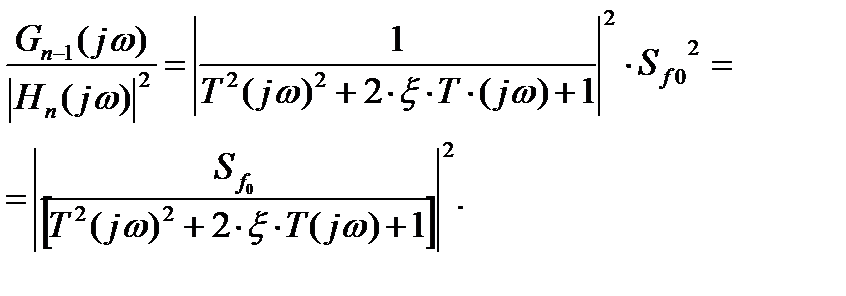
Из этого соотношения следует, что

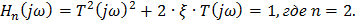
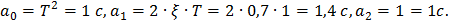
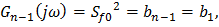
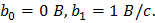
Для n = 2 имеем

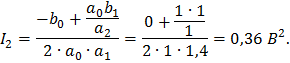
Используя выражение (2.17) получим

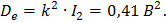
Заметим, что найденное значение дисперсии характеризует погрешность результата измерения для условия .

 

 

3 Разработка алгоритма обработки многократных измерений

 

3.1 Многократные измерения и их обработка

 

Качество результата измерения определяется величиной содержащейся в нем погрешности. Поэтому при измерении необходимо стремиться к тому, чтобы получить результат с минимальной погрешностью. Основными факторами, вызывающими появление погрешности результата измерения являются: метод измерения, несовершенство средства измерения, влияние условий измерения на параметры средств измерений и на измеряемую физическую величину и ее характер. Поэтому для получения высокоточных результатов необходимо создавать средства измерения, которые обладали бы малой инерционностью 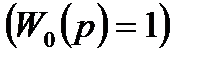и минимальным отклонением коэффициента чувствительности от номинального значения , а также устойчивостью к внешним возмущающим воздействиям.

В реальных условиях при решении конкретных измерительных задач результат все равно будет содержать погрешность, поэтому для ее оценки и исключения из результата измерения необходимо использовать эффективные алгоритмы. Одним из путей решения этой проблемы - это применение многократных измерений и последующая обработка их результатов.

Многократное измерение - это измерение, при котором результат представляется совокупностью нескольких возможных значений. Результат измерения по своей природе всегда является случайной величиной. По определению каждая случайная величина связана с некоторым множеством возможных значений (конечным - для дискретной величины, несчетным -для непрерывной случайной величины). При измерении результат принимает одно из значений этого множества случайным образом. Повторяя измерения можно получить результаты многократных измерений.

Процесс многократных измерений достаточно длительный по времени, причем каждое возможное значение появляется в определенный фиксированный момент времени. Это означает, что совокупность возможных результатов измерений при многократных измерениях представляет упорядоченную совокупность - некоторую функцию дискретного аргумента времени, или иначе - последовательность. В практике измерений количество дискретных значений аргумента можно представить как , и , где - возможное значение результата измерения в момент t_k. Такую последовательность принято называть «выборкой объема n».

Последовательность , , содержит больше информации об измеряемой физической величине, чем однократное измерение, при котором результат принимает одно возможное значение, поэтому на ее основе можно получить более точную оценку значения измеряемой физической величины.

Таким образом, задача обработки результатов многократных измерений сводится к тому, чтобы построить такое преобразование случайной последовательности , и , которое обеспечивало бы оптимальную оценку значения измеряемой физической величины. Аналитическое представление такого преобразования называется алгоритмом обработки многократных измерений.

Исходными данными для построения алгоритма обработки многократных измерений являются: математическая модель измеряемой величины в виде ,

где - постоянные коэффициенты,

- базисные функции,

- план измерений, и допущение о равноточности и некоррелированности многократных измерений.

 

3.2. Исходные данные и общие выражения для вектора оценки и ковариационной матрицы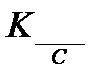

Математическая модель измеряемой величины являются параметрической и имеет следующий вид

,

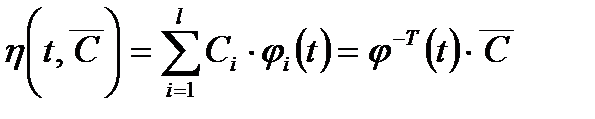где - вектор коэффициентов,

-транспонированные вектор – столбец базисных функций.

План измерений задается и имеет следующую структуру: , -дискретные значения аргумента t, в которых производится однократное измерение функции отклика. Таким образом, объем многократных измерений по данному плану равно 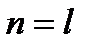. Предполагается, что многократные измерения являются равноточными и некоррелированными.

Пусть

 

- вектор многократных измерений

- матрица базисных функций размера

.

Решение:

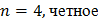
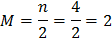
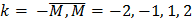
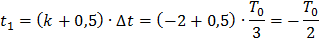
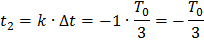
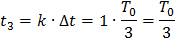
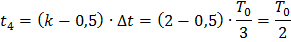
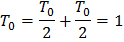
3.3 Определение выражений для оценок коэффициентов и их дисперсии

 

Базисными функциями модели являются , .

Найдем элементы матрицы базисных функций:

 

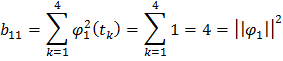
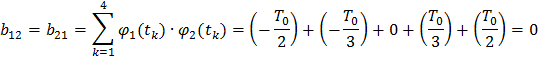
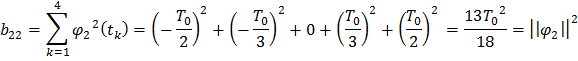
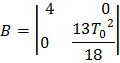
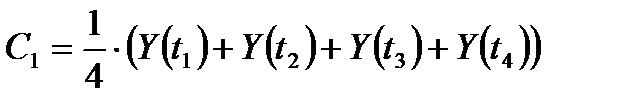
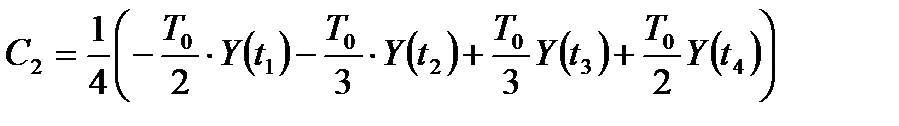
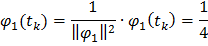
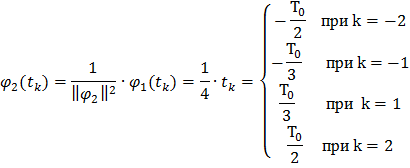
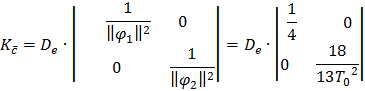
Найдем выражение для дисперсии оценок коэффициентов

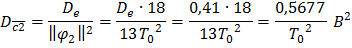
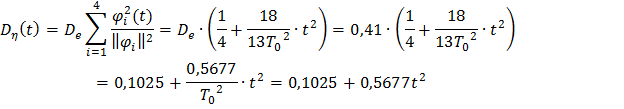
Графическое изображение дисперсии показано на рисунке 4.

 

Рисунок 4. График дисперсии оценки математической модели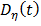

СПИСОК ПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

 

1 Владимирова, Т.М. Аналитические методы определения погрешности результата измерения: [Текст] / метод. указания к выполнения практических работ / Т.М. Владимирова. – Архангельск: АГТУ, 2008. – 23 с.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: