 |
Выбор оптимального портфеля
|
|
|
|
Оптимальный портфель – это единственный из эффективных портфелей, который является наилучшим для конкретного инвестора.
При выборе оптимального портфеля решаются 2 задачи:
1. определение эффективного множества портфелей,
2. выбор из этого эффективного множества единственный наилучший для конкретного инвестора.
Эффективные и оптимальные портфели.
Плоскость «Риск-доходность».
σ – риск; а – ожидаемая доходность
Кривые 
называют кривыми безразличия «риск-доходность». Это индивидуальные характеристики конкретных инвесторов. Другие инвесторы могут иметь иные предпочтения, но абсолютное большинство инвесторов при возрастании риска повышают требовательность к доходности. Портфель, оптимальный с точки зрения инвестора, соответствует точке касания кривой (дуга ANME), характеризующей эффективное множество портфелей и кривой безразличия конкретного инвестора (
) – точка N на рис.1. Эта точка соответствует наиболее высокому уровню удовлетворенности, которого может достигнуть данный инвестор. Другой инвестор может выбрать другой портфель.
12. Линия рынка капитала, линия рынка ценных бумаг. β -коэффициент
Линия рынка капитала – это линия RMZ на рис.1. Точка N, в которой кривая безразличия касается границы эффективного множества, отражает выбор оптимального портфеля, обеспечивающего инвестору самую высокую доходность при величине риска 
. Однако инвестор может сделать лучший выбор, чем портфель N. Он может достигнуть более высокой кривой безразличия, если в дополнение к множеству рисковых портфелей, воспользуется безрисковым активом, который обеспечивает гарантированную доходность 
- на оси доходности эта точка, из которой исходит линия рынка капитала RMZ. Включение безрискового актива в свой портфель позволяет достигнуть комбинации риска и доходности на прямой линии рынка капитала. Используя новые возможности, инвестор перейдет из точки N в точку R, которая находится на более высокой кривой безразличия. Доходность такого портфеля определяется:
|
|
|
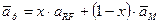, где
- доходность портфеля, включающего безрисковый актив,
- доля безриского актива в портфеле,
- доходность безриского актива,
- доходность портфеля рисковых активов.
, где
- среднее квадратическое отклонение доходности рискового портфеля.
В модели оценки доходности финансовых активов САРМ рисковость ценных бумаг измеряется ее β – коэффициентом. Он характеризует изменчивость доходности конкретной акции относительно доходности рынка ценных бумаг. Некая средняя акция имеет β=1. Акция, изменчивость доходности которой больше, чем в среднем на рынке, имеет β больше 1. Акция, изменчивость доходности которой меньше, чем в среднем на рынке, имеет β меньше 1.
Уравнение связи между риском и доходностью акции называется уравнением рынка ценных бумаг:
, где
- требуемая доходность i-ой акции (ставка дисконтирования),
- безрисковая доходность (доходность государственных ценных бумаг, депозитов в наиболее надежных банках),
- требуемая доходность рыночного портфеля, состоящего из всех акций, которыми торгуют на рынке (среднерыночный уровень доходности),
- β – коэффициент i-ой акции.
- премия за риск владения акцией.
13. Концепция β – коэффициента
Показатели средней акции по определению должны варьироваться в соответствии с изменением ситуации на рынках, измеряемыми биржевыми индексами. Средняя акция имеет β – коэффициент = 1. Это означает, что при изменении ситуации на рынке рост или снижение на один процентный пункт характеристики акции меняются в том же направлении на один процентный пункт. Если акция имеет β – коэффициент = 0,5, то её характеристики будут меняться в два раза медленнее, чем в среднем на рынке. Портфель, состоящий из таких акций, будет иметь риск, равный половине риска портфеля из всех акций рынка, имеющих β – коэффициент = 1.
|
|
|
Если β – коэффициент = 2, то изменчивость характеристик акций в два раза выше по сравнению со средней акцией, поэтому портфель, состоящий из таких акций, имеет риск в 2 раза выше среднего портфеля.
Формула β – коэффициента портфеля ценных бумаг:
, где
- доля i -ой ценной бумаги в портфеле,
- β – коэффициент,
n – число ценных бумаг в портфеле.
Добавление в портфель акции, имеющей β>1, увеличивает значение 
и повышает рисковость портфеля (или наоборот).
Расчет β – коэффициентов.
Величина фактической доходности конкретной акции и доходности на рынке акций в среднем по календарным периодам оказываются взаимосвязаны. Эта взаимосвязь выражается линейной зависимостью, которую можно получить путем статистической обработки данных биржевой статистики:
, где
- доходность i -ой акции,
- доходность рынка в среднем,
, - коэффициенты уровня регрессии,
Е – случайная ошибка.
|
|
|
