 |
Частные термодинамические процессы.
|
|
|
|
Реферат по Теплотехники
Выполнил Студент: Сат А. Э.
Группа: МНТ -14
Проверил: Павловец В.И.
Новокузнецк 2016
Содержание
Тема 2.
2.1.Политропный процесс.
2.2.Частные термодинамические процессы.
2.3.Теплоемкость.
2.4.Расчет количества теплоты, необходимой для нагрева физических тел.
Тема 3.
3.1.Теплообменные процессы и установки в транспортно-технологических комплексах.
3.2.Конвективный режим работы теплотехнических агрегатов.
3.3.Сложный теплообмен в теплотехнических устройствах.
3.4.Радиационный режим работы промышленных печей.
Тема 4.
4.1.Использование топлива в металлургии, энергетике, транспортно-технологических комплексах и в других отраслях промышленности.
4.2.Экологические аспекты горения топлива.
4.3.Мероприятия, направленные на повышение эффективности сжигания топлива.
4.4.Транспортно-технологические машины и системы в структуре топливно-энергетического комплекса.
Тема 2.
Политропный процесс.
Политропный процессом называется термодинамический процесс, в процессе которого удельная теплоёмкость газа остаётся неизменной.
В политропном процессе распределение подводимого тепла между изменением внутренней энергии и работой газа, характеризуемое величиной
,
остается неизменным, поскольку dq = c×dT и
.
Где буквой с обозначается постоянная для этого процесса теплоемкость газа.
Уравнение политропы в 
– диаграмме может быть выведено из аналитических выражений первого закона термодинамики
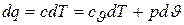
и 
откуда получаем
и 
.
Разделив второе равенство на первое, имеем
.
Обозначая постоянную для данного процесса величину 
через n, получаем
,
а после разделения переменных
|
|
|
.
Интегрируя полученное дифференциальное уравнение, находим
и окончательно
. (4.22)
В этом уравнении величина n называется показателем политпропы. Будучи постоянным для каждого конкретного процесса, численное значение этого показателя определяет характер процесса.
Так, при n = 0 уравнение политропы принимает вид
p = const,
т.е. превращается в уравнение изобары. Следовательно, изобара представляет собой политропу с n = 0.
Аналогично этому легко показать, что изотерма – это политропа с показателем n = 1, а адиабата – это политропа с показателем n = k.
Согласно определению политропного процесса изохора также является политропой, поскольку для нее с = сJ = const. Показатель политропы для изохорного процесса можно определить следующим образом.
Из уравнения политропы следует, что
.
Так как для линии J = const должно быть
.
То 
.
Все соотношения, вытекающие из уравнения политропы 
, должны быть аналогичными соотношениям, вытекающим из уравнения адиабаты 
, и получаются из них путем замены показателя адиабаты k на показатель политропы n.
Таким образом, связь между параметрами газа в двух состояниях при политропном процессе выражается формулами
, (4.23)
а формулы для работы изменения объема газа в политропном процессе имеют вид
(4.24)
и 
. (4.25)
Согласно первому закону термодинамики для политропного процесса
.
Сравнивая полученное выражение с формулой
,
находим зависимость
или учитывая, что 
, имеем окончательно
. (4.26)
Таким образом, в зависимости от показателя политропы теплоемкость газа в политпропных процессах может иметь различные значения, что наглядно иллюстрируется графиком с = f (n), приведенным на рисунке 4.5. В частности, для изохорного процесса, когда 
, с = сJ; для изобарного процесса, когда n = 0, c = cp; для изотермического процесса, когда n = 1, 
; наконец, для адиабатного процесса, когда n = k, c = 0.
Далее график показывает, что на участке 1< n < k, т.е. для политропных процессов, расположенных между изотермой и адиабатой, значение теплоемкости отрицательно. Это объясняется тем, что на указанном участке числитель и знаменатель выражения
|
|
|
имеют разные знаки.
Действительно, при политропном расширении в этом случае тепло подводится, но температура понижается; при политропном сжатии, наоборот, тепло отводится, но температура повышается.
Логарифмируя уравнение политропы , получаем
.
Это отношение в логарифмической системе координат изображается прямой линией (например, 1–2 на рис. 4.6). Поэтому, для того чтобы установить, является ли политропным процесс, изображенный в –диаграмме какой – либо линией, следует несколько точек этой линии перенести в логарифмическую систему координат. Если все точки расположатся на одной прямой, то график изображает политропный процесс с показателем
.
Частные термодинамические процессы.
Термодинамическим процессом называется процесс перехода рабочего тела (газа или пара) из одного состояния начального в другое (конечное) состояние.
Термодинамические процессы состоят из четырех процессов изменения состояния идеального газа:
1) изохорного, который протекает при постоянном объеме;
2) изобарного, который протекает при постоянном давлении;
3) изотермического, который протекает при постоянной температуре;
4) адиабатного, который протекает без теплообмена с окружающей средой.
Теплоемкость.
Теплоёмкостью тела это физическая величина, которая обозначается C. Она определяет отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:
Единицей измерения теплоёмкости в системе СИ является Дж/К.
Теплоемкость вещества это теплоемкость единицы массы данного вещества. Единицей измерения является Дж/(кг К).
Молярная теплоемкость это теплоемкость 1 моля данного вещества. Единицей измерения молярной теплоемкости является Дж/(моль К).
Теплоемкость определяется для веществ в трех агрегатных состояниях (твердые тела, жидкости, газы) и для соединений частиц и квазичастиц.
Если рассматривать не конкретное физическое тело, а вещества то различают удельную теплоёмкость — теплоёмкость единицы массы этого вещества и молярную — теплоёмкость одного моля этого вещества.
|
|
|
2.4. Расчет количества теплоты, необходимой для нагрева физических тел.
|
|
|
