Емкостное сопротивление в цепи переменного тока

Введение

Цель данного проекта состоит в том, чтобы получить достаточно полное представление об электрических цепях и их составных элементах, их математических описаниях, основных методах анализа и расчета этих, т.е. в создании научной базы для последующего изучения различных специальных электротехнических дисциплин.

Задачи проекта заключаются в освоении теории физических явлений, положенных в основу создания и функционирования различных электротехнических устройств, а также в привитии практических навыков использования методов анализа и расчета электрических цепей для решения широкого круга задач.

В данном проекте рассмотрены три задачи:

Первая задача на знание законов Кирхгофа и нахождение баланса мощностей;

Вторая задача на нахождение емкостное сопротивление в цепи переменного тока;

Третья задача на решение задач по переходным процессам в линейных цепях классическим методом.

 

1.
Законы Кирхгофа. Баланс мощностей

 

Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным ветвям. Значения токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.

Первый закон Кирхгофа устанавливает зависимость между токами для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

∑ I =0

Формула 1. Первый закон Кирхгофа.

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла, - с противоположным знаком (отрицательным).

Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

 

∑ E = ∑ IR

 

Формула 2. Второй закон Кирхгофа.

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.

Все расчеты в электрических цепях проверяют балансом мощностей.

Баланс основан на законе сохранения и превращения энергии: сколько энергии выработали источники, столько же ее нагрузки должны потребить. Вместо энергии в балансе можно использовать мощность. Выработанная мощность всеми источниками должна быть равна суммарной мощности, расходуемой в нагрузках.

Баланс мощностей можно сформулировать так: алгебраическая сумма мощностей источников, должна быть равна арифметической сумме мощностей нагрузок. Если направление ЭДС и направление тока ветви не совпадают, то составляющая мощности этого источника в балансе мощностей берется со знаком «минус».

1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа.

I Закон Кирхгофа:

 

·   а - I₁+I₃-I₄=0

·   б - I₄-I₅+I₆=0

·   в - I₁+I₂-I₆=0

I₁R₁-I₂R₂+I₃R₃=E₁-E₂

I₂R₂+I₆R₆+I₅R₅=E₂

I₃R₃+I₄R₄+I₅R₅=0

 

2. Определить токи в ветвях методом контурных токов.

 

I₁₁(R₁+R₂+R₃) - I₂₂R₂+I₃₃R₃=E₁-E₂

I₂₂(R₂+R₅+R₆) - I₁₁R₂+I₂₂R₅=E₂₃₃(R₃+R₄+R₅) - I₁₁R₃+I₂₂R₅=0

 

I₁₁-6I₂₂+9I₃₃= -95

(-6) I₁₁+15I₂₂+6I₃₃=110

I₂₂+6I₂₂+23I₃₃=0

 

 

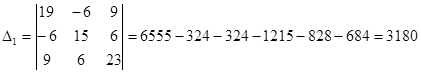
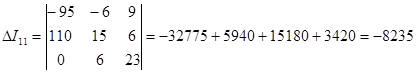
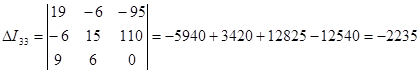
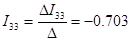₁=I₁₁=-2.59A₂=-I₁₁+I₂₂=-3.293A₃=I₁₁+I₃₃=-3.293A₄=I₃₃=-0.703A₅=I₂₂+I₃₃=5.876A₆=I₂₂=6.579A

 

Проверка: 

а) - I₁+I+I₄=0

 

2.59-3.293+0.703=0

 

3. Определить токи в ветвях методом узловых потенциалов.

 

φ₁=0

φ _a=(g₁+g₄+g₃) - φ_бg₄ - φ_вg₁=E₁g₁

φ_б=(g₄+g₅+g₆) - φ_аg₄ - φ_вg₆=0

φ_a=(g₁+g₂+g₆) - φ_аg₁ - φ_бg₆=E₁g₁+E₂g₂₁=1/R₁=0.25 См g₄=1/R₄=0.125 См₂=1/R₃=0.167 См g₅=1/R₅=0.167 См₃=1/R₃=0.111 См g₆=1/R₆=0.333 См

,486 φ_a-0.125 φ_б-0,25 φ_в=-3.75

φ_а+0,625 φ_б-0,333 φ_б=0

,254 φ_а-0,333 φ_б+0,75 φ_в=22,12

 

 

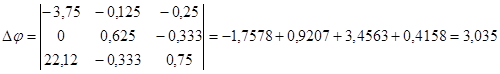
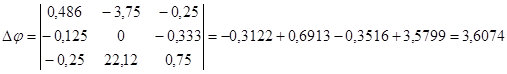
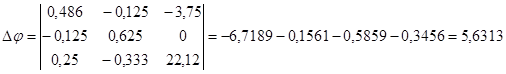
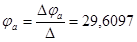
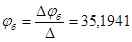
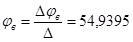
I₁=(φ_a - φ_в+Е₁) g₁=-2.58 A₂=(-φ_в+Е₂) g₂=9.195 A₃=-φ_a*g₃=-3.287 A₄=(φ_a-φ_б) g₄=-0.698 A₅=φ_б*g₅=5.877 A₆=(φ_в-φ_б) g_в=6.575 A

Емкостное сопротивление в цепи переменного тока

кирхгоф мощность емкостный сопротивление

Емкостное сопротивление это сопротивление переменному току, которое оказывает электрическая емкость. Ток в цепи с емкостью опережает напряжение по фазе на 90 градусов. Емкостное сопротивление является реактивным, то есть потерь энергии в нем не происходит как, например, в активном сопротивлении. Емкостное сопротивление обратно пропорционально частоте переменного тока.

Проведем эксперимент, для этого нам понадобится. Конденсатор лампа накаливания и два источника напряжения один постоянного тока другой переменного. Для начала построим цепь, состоящую из источника постоянного напряжения, лампы и конденсатора все это включено последовательно.

При включении тока лампа вспыхнет на короткое время, а потом погаснет. Так как для постоянного тока конденсатор имеет большое электрическое сопротивление. Оно и понятно ведь между обкладками конденсатора находится диэлектрик, через который постоянный ток не способен пройти. А вспыхнет лампа по тому, что в момент включения источника постоянного напряжения идет кратковременный импульс тока, заряжающий конденсатор. А раз ток идет значит и лампа светится.

Теперь в этой цепи заменим источник постоянного напряжения на генератор переменного. При включении такой цепи мы обнаружим, что лампа буде светится непрерывно. Происходит это по тому, что конденсатор в цепи переменного тока заряжается за четверть периода. Когда напряжение на нем достигнет амплитудного значения, напряжение на нем начинает уменьшаться, и он будет, разряжается следующие четверть периода. В следующие пол периода процесс повторится снова, но напряжение в этот раз уже будет отрицательным.

Таким образом, в цепи непрерывно течет ток хотя он и меняет при этом свое направление дважды за период. Но через диэлектрик конденсатора заряды не проходят. Как же это происходит.

Представим себе конденсатор, подключаемый к источнику постоянного напряжения. При включении, источник убирает электроны с одной обкладки, тем самым создавая на ней положительный заряд. А на второй обкладке добавляет электронов, создавая тем самым равный по величине, но противоположный по знаку отрицательный заряд. В момент перераспределения зарядов в цепи протекает ток заряда конденсатора. Хотя электроны при этом не движутся через диэлектрик конденсатора.

Если теперь из цепи исключить конденсатор, то лампа будет светить ярче. Это говорит о том, что емкость создает сопротивление, току ограничивая его величину. Происходит это из-за того что при заданной частоте тока значение ёмкости мало и она не успевает накопить достаточно энергии в виде зарядов на своих обкладках. И при разряде будет протекать ток меньше чем способен развить источник тока.

Отсюда следует, что емкостное сопротивление зависит как от частоты, так и от величины емкости конденсатора.

Дано:

 

 

R= 40 ом

X_L= 60 ом

X_C= 30 ом= 50 ом

Z-? I -?φ -?

Реактивное сопротивление - электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).

 

 

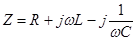
Индуктивное сопротивление (X_L) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи:

 

 

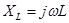
Ёмкостное сопротивление (X_C). Величина ёмкостного сопротивления зависит от ёмкости элемента C и также частоты протекающего тока ʄ:

 

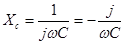
Исходя из всего вышенаписанного, приходим к записи:

 

 

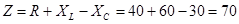
Находим значение комплексного тока. Комплексный ток находится по формуле:

 

 

Находим коэффициент мощности по формуле:

 

 

Поделиться:

Воспользуйтесь поиском по сайту: