 |
Метод доказательства «от противного»
|
|
|
|
Дополнительное построение
Продли медиану
Характеристика метода. Довольно часто, когда в условии задачи фигурирует медиана треугольника, бывает полезным продлить ее за точку, лежащую на стороне треугольника, на отрезок, равный самой медиане. Полученная новая точка соединяется с вершиной (вершинами) исходного треугольника, в результате чего образуются равные треугольники. Равенство соответствующих элементов этих треугольников помогает найти неизвестную величину или доказать предложенное утверждение.
|
|
Задача. Докажите, что треугольник является равнобедренным, если совпадают проведенные из одной и той же вершины медиана и биссектриса.
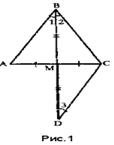
Решение. Рассмотрим треугольник ABC (рис. 1). Пусть отрезок BM – его медиана и биссектриса. Продлим BM на отрезок MD = BM. Образовались равные треугольники AMB и MCD (1-й признак равенства треугольников).
Из равенства этих треугольников имеем:
(1) AB = CD и (2) Ð 1 = Ð 3.
 |
Используя равенство (2) и то, что Ð 1 = Ð 2 (по условию), получим, что треугольник BCD равнобедренный, а, следовательно, BC = CD. Используя полученный вывод и равенство (1) доказываем, что AB = BC, откуда следует истинность утверждения задачи.
Принцип непрерывности
|
|
Характеристика метода. Пусть величина k (угол, длина, площадь) зависит от положения точки X на отрезке (ломаной или другой линии). Если при одном положении X на отрезке k < 0, а при другом положении X на отрезке k > 0, то найдется такое положение X на этом отрезке, при котором k = 0.
Задача. В равностороннем треугольнике ABC проведена медиана AA 1. Есть ли такая точка X на AA 1, из которой отрезок BC виден под прямым углом.
Решение. Будем искать такое положение точки X, при котором Ð BXC = 90°. Начнем мысленно перемещать точку X по отрезку AA 1 от A к A 1. Обозначим величину угла BXC за j. Когда точка X находится достаточно близко от точки A (рис. 2), тогда мало отличается от 6°, а поэтому j< 90°. Когда точка X находится достаточно близко от (рис. 3), тогда j.
|
|
|
мало отличается от 180°, а поэтому j> 90°. Значит при каком-то положении точки X на AA 1 j.
 |  | ||
= 90°.
Метод доказательства «от противного»
Характеристика метода. Имеем для доказательства утверждения вида A Þ B (A – условие, B – заключение). Суть доказательства данным методом состоит в следующем:
1) Предполагаем, что заключение B не выполняется.
2) Путем логических рассуждений приходим к тому, что условие A не выполняется, т. е. получаем противоречие с условием.
3) Дальнейший анализ показывает, что причина полученного противоречия кроется в первоначальном предположении.
4) Делаем вывод, что это предположение неверно и, следовательно, заключение B выполняется (что и требовалось доказать).
Задача. Какое наибольшее число острых углов может быть в выпуклом многоугольнике?
Решение. Легко показать, что три острых угла в многоугольнике может быть (например, в треугольнике). Все попытки построить какой-нибудь выпуклый n -угольник с четырьмя острыми углами оказываются тщетными. Возникает гипотеза: максимальное количество острых углов выпуклого многоугольника – три. Докажем ее.
1) Пусть найдется выпуклый многоугольник с большим числом углов, например, с четырьмя.
2) В этом случае сумма четырех острых углов будет меньше, чем 90°•4 или 180°•2. Сумма же остальных n – 4 углов будет меньше, чем 180°•(n – 4). Тогда сумма всех углов n -угольника меньше, чем 180°•2 + 180°•(n – 4) = 180°•(n – 2), а это невозможно для выпуклого n -угольника (сумма его углов равна 180°•(n – 2)).
3) Полученное противоречие кроется в исходном предположении.
4) Наше предположение относительно существования четырех (а как показывает анализ рассуждений и большего количества) острых углов неверно. Следовательно, максимальное количество острых углов выпуклого n -угольника – три.
|
|
|
Доказательство выдвинутой гипотезы завершает решение задачи.
|
|
|


