 |
Уравновешивание и равномерность хода двигателя
|
|
|
|
АВТОМОБИЛЬНЫЕ ДВИГАТЕЛИ
Кинематика и динамика поршневого ДВС
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
 «НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯРОСЛАВА МУДРОГО»
«НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯРОСЛАВА МУДРОГО»
АВТОМОБИЛЬНЫЕ ДВИГАТЕЛИ
Кинематика и динамика поршневого ДВС
Учебное пособие к курсовому проекту по дисциплине
«Автомобили и двигатели: Автомобильные двигатели»
Специальность 190601 «Автомобили и автомобильное хозяйство»
УДК 629. 113. 004 Печатается по решению
РИС НовГУ
Автомобильные двигатели: 2. Кинематика и динамика поршневого ДВС: Учебное пособие к курсов. проекту. / Авт.- сост.: А. В. Капустин, Н.Н. Заводов; НовГУ им. Ярослава Мудрого. – Великий Новгород, 2011. -? с.
Настоящее учебное пособие является второй частью пособия по проектированию поршневых двигателей внутреннего сгорания и включает разделы кинематического, динамического расчета и графического анализа кривошипно-шатунного механизма, расчета неравномерности крутящего момента, равномерности хода двигателя и уравновешенности ДВС.
Учебное пособие предназначено для студентов специальности 190601 – автомобили и автомобильное хозяйство, изучающих дисциплину «Автомобили и двигатели: Автомобильные двигатели» и отвечает требованиям Государственного образовательного стандарта высшего профессионального образования (ГОС ВПО) по направлению подготовки дипломированного специалиста 190601 – «Автомобилии автомобильное хозяйство».
Рецензенты: Н.М. Андрианов,
доктор техн. наук, профессор
Я.П. Энсон
канд. техн. наук, доцент
|
|
|
СОДЕРЖАНИЕ
1. Кинематический расчет………………………….
2. Динамический расчет…………
3 Уравновешивание и равномерность хода двигателя………
Приложение
Список литературы..
Кинематический расчет
В общем случае расчет выполняется для центрального кривошипно-шатунного механизма и ниже изложена методика расчета такого КШМ.
По желанию студента при соответствующем обосновании можно выполнять расчет дезаксиального (смещенного) КШМ или КШМ с прицепным шатуном. В этом случае следует пользоваться дополнительной учебной литературой.
Перемещение поршня (мм) определяется по формуле
Sn = R [(1 – cosj) +  (1 – cos2j)], (1.1)
(1 – cos2j)], (1.1)
где R – радиус кривошипа, мм;
 – характеристика КШМ (отношение радиуса кривошипа к длине шатуна
– характеристика КШМ (отношение радиуса кривошипа к длине шатуна  = R/Lш);
= R/Lш);
j – угол поворота коленчатого вала.
За начало отсчета угла j принято положение КШМ в верхней мертвой точке (ВМТ), начало впуска для четырехтактных ДВС. Положительное вращение коленчатого вала – по часовой стрелке.
Значение выражения [(1 – cosj) +  (1 – cos2j)] можно принять из таблицы 1.1.
(1 – cos2j)] можно принять из таблицы 1.1.
Радиус кривошипа принять из теплового расчета R=S/2, S – ход поршня.
Значение  должно соответствовать принятому
должно соответствовать принятому  в тепловом расчете при построении индикаторной диаграммы.
в тепловом расчете при построении индикаторной диаграммы.
Скорость поршня Vп, м/с рассчитывается по формуле
(размерность R – м)
Vп = w×R× (sinj +  × sin2j), (1.2)
× sin2j), (1.2)
гдеw – угловая скорость вращения кривошипа, рад/с.
Значение выражения (sinj +  × sin2j) принимается из таблицы1.2.
× sin2j) принимается из таблицы1.2.
Ускорение поршня jn, м/сек2 рассчитывается по формуле
jn = w2 × R (cosj + l × cos2j), (1.3)
где значение (cosj+l×cos2j) можно выбрать из таблицы 1.3.
Таблица 1.1
| j° | Значения (1 – cos j) +  (1 – cos 2j) при l (1 – cos 2j) при l
| j° | |||||||
| 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | ||
| 0,0000 0,0188 0,0743 0,1640 0,2836 0,4276 0,5900 0,7640 0,9428 1,1200 1,2900 1,4480 1,5900 1,7132 1,8156 1,8960 1,9537 1,9884 2,0000 | 0,0000 0,0190 0,0749 0,1653 0,2857 0,4306 0,5938 0,7684 0,9476 1,1250 1,2948 1,4524 1,5938 1,7162 1,8177 1,8973 1,9543 1,9886 2,0000 | 0,0000 0,0191 0,0755 0,1665 0,2877 0,4335 0,5975 0,7728 0,9525 1,1300 1,2997 1,4568 1,5975 1,7191 1,8197 1,8985 1,9549 1,9887 2,0000 | 0,0000 0,0193 0,0761 0,1678 0,2898 0,4364 0,6013 0,7772 0,9573 1,1355 1,3045 1,4612 1,6013 1,7220 1,8218 1,8998 1,9555 1,9889 2,0000 | 0,0000 0,0194 0,0767 0,1690 0,2918 0,4394 0,6050 0,7816 0,9622 1,1400 1,3094 1,4656 1,6050 1,7250 1,8238 1,9010 1,9561 1,9890 2,0000 | 0,0000 0,0196 0,0773 0,1703 0,2939 0,4423 0,6088 0,7860 0,9670 1,1450 1,3142 1,4700 1,6088 1,7279 1,8259 1,9023 1,9567 1,9892 2,0000 | 0,0000 0,0197 0,0779 0,1715 0,2960 0,4452 0,6125 0,7905 0,9719 1,1500 1,3191 1,4745 1,6125 1,7308 1,8280 1,9035 1,9573 1,9893 2,0000 | 0,0000 0,0199 0,0784 0,1728 0,2980 0,4482 0,6163 0,7949 0,9767 1,1550 1,3239 1,4789 1,6163 1,7338 1,8300 1,9048 1,9578 1,9895 2,0000 |
|
|
|
Таблица 1.2
| j° | Знак | Значения (sinj +  ×sin2j) при λ ×sin2j) при λ
| Знак | j° | |||||||
| 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | ||||
| + + + + + + + + + + + + + + + + + + + | 0,0000 0,2146 0,4191 0,6039 0,7610 0,8842 0,9699 1,0168 1,0258 1,0000 0,9438 0,8626 0,7621 0,6478 0,5246 0,3961 0,2649 0,1326 0,0000 | 0,0000 0,2164 0,4224 0,6083 0,7659 0,8891 0,9743 1,0201 1,0276 1,0000 0,9420 0,8593 0,7577 0,6429 0,5197 0,3917 0,2616 0,1308 0,0000 | 0,0000 0,2181 0,4256 0,6126 0,7708 0,8940 0,9786 1,0233 1,0293 1,0000 0,9403 0,8561 0,7534 0,6380 0,5148 0,3874 0,2584 0,1291 0,0000 | 0,0000 0,2198 0,4288 0,6169 0,7757 0,8989 0,9829 1,0265 1,0310 1,0000 0,9386 0,8529 0,7491 0,6331 0,5099 0,3831 0,2552 0,1274 0,0000 | 0,0000 0,2215 0,4320 0,6212 0,7807 0,9039 0,9872 1,0297 1,0327 1,0000 0,9369 0,8497 0,7448 0,6281 0,5049 0,3788 0,2520 0,1257 0,0000 | 0,0000 0,2232 0,4352 0,6256 0,7856 0,9088 0,9916 1,0329 1,0344 1,0000 0,9352 0,8465 0,7404 0,6232 0,5000 0,3744 0,2488 0,1240 0,0000 | 0,0000 0,2249 0,4384 0,6299 0,7905 0,9137 0,9959 1,0361 1,0361 1,0000 0,9335 0,8433 0,7361 0,6183 0,4951 0,3701 0,2456 0,1223 0,0000 | 0,0000 0,2266 0,4416 0,6342 0,7954 0,9186 1,0002 1,0393 1,0378 1,0000 0,9318 0,8401 0,7318 0,6134 0,4902 0,3658 0,2424 0,1206 0,0000 | – – – – – – – – – – – – – – – – – – – |
Таблица 1.3
| j° | Знак | Значения (cos j + l cos 2j) при l | Знак | j° | |||||||
| 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | ||||
| + + + + + + + + – – – – – – – – – – – | 1,2400 1,2103 1,1235 0,9860 0,8077 0,6011 0,3800 0,1582 0,0519 0,2400 0,3991 0,5258 0,6200 0,6845 0,7243 0,7460 0,7559 0,7593 0,7600 | 1,2500 1,2197 1,1312 0,9910 0,8094 0,5994 0,3750 0,1505 0,0613 0,2500 0,4085 0,5335 0,6250 0,6862 0,7226 0,7410 0,7482 0,7499 0,7500 | 1,2600 1,2291 1,1389 0,9960 0,8111 0,5977 0,3700 0,1428 0,0707 0,2600 0,4179 0,5412 0,6300 0,6879 0,7209 0,7360 0,7405 0,7405 0,7400 | 1,2700 1,2385 1,1465 1,0010 0,8129 0,5959 0,3650 0,1352 0,0801 0,2700 0,4273 0,5488 0,6350 0,6897 0,7191 0,7310 0,7329 0,7311 0,7300 | 1,2800 1,2479 1,1542 1,0060 0,8146 0,5942 0,3600 0,1275 0,0895 0,2800 0,4367 0,5565 0,6400 0,6914 0,7174 0,7260 0,7252 0,7217 0,7200 | 1,2900 1,2573 1,1618 1,0110 0,8163 0,5925 0,3550 0,1199 0,0989 0,2900 0,4461 0,5641 0,6450 0,6931 0,7157 0,7210 0,7176 0,7123 0,7100 | 1,3000 1,2667 1,1695 1,0160 0,8181 0,5907 0,3500 0,1122 0,1083 0,3000 0,4555 0,5718 0,6500 0,6949 0,7139 0,7160 0,7099 0,7029 0,7000 | 1,3100 1,2761 1,1772 1,0210 0,8198 0,5890 0,3450 0,1045 0,1177 0,3100 0,4649 0,5795 0,6550 0,6966 0,7122 0,7110 0,7022 0,6935 0,6900 | + + + + + + + + – – – – – – – – – – – |
|
|
|
Расчеты по формулам (1.1 – 1.3) можно выполнять через j=30° поворота коленчатого вала (ПКВ). По полученным значениям следует построить графики Sn = f(j), Vn = f(j), jn = f(j).
Динамический расчет
Динамическим расчетом определяют силы, действующие в КШМ, в зависимости от угла поворота коленчатого вала.
Силы давления газов, действующие на площадь поршня, для упрощения динамического расчета заменяют одной сосредоточенной силой, направленной по оси цилиндра и приложенной к оси поршневого пальца.
Ее значение определяют произведением перепада давлений (над поршнем и под поршнем) на площадь поршня по формуле
Рг = 1000·(рг – р0)×Fn, кН (2.1)
где рг– давление газов над поршнем, МПа;
р0 – давление газов под поршнем, равное приблизительно атмосферному давлению, МПа;
Fn – площадь поршня в м2.
Для анализа динамической нагруженности элементов КШМ индикаторную диаграмму из координат р-V перестраивают в развернутую индикаторную диаграмму в координатах р-φ. Это перестроение можно выполнить графически по методу профессора Ф.А. Брикса или аналитически, используя зависимость (1.1) и уравнение политропного процесса.
Учитывая развитие вычислительных методов, изложим методику аналитического метода перестроения индикаторной диаграммы четырехтактного двигателя.
При положении поршня в ВМТ в момент начала впуска давление над поршнем равно давлению остаточных газов – рr, принятому в тепловом расчете. В конце процесса впуска давление рг равно давлению ра. В промежуточных положениях КШМ между ВМТ и нижней мертвой точкой (НМТ) начиная с φ=30° значения рг можно принимать рг=ра.
В процессе сжатия от φ=180° до φ= (360-φс¢) надпоршневое давление рг можно рассчитать по уравнению политропного процесса сжатия с принятым в тепловом расчете показателем политропы n1
|
|
|
рг·Vх  = ра·Vа
= ра·Vа  , (2.2)
, (2.2)
где Vx – текущий надпоршневой объем;
Vа – полный объем цилиндра.
Vа= Vh +Vc, (2.3)
где Vh и Vc – рабочий и полный объемы.
Vx= Vс+Vh·[(1 – cosj) + λ·(1 – cos2j)/4]/2 (2.4)
После подстановки (2.3) и (2.4) в (2.2), последующих алгебраических преобразований с учетом того, что Vа/Vс=ε, а Vh/Vс=ε-1 получим расчетное выражение
 , (2.5)
, (2.5)
При φ=360°давление принимают из теплового расчета при скруглении индикаторной диаграммы рс״≈1,2·рс..
По экспериментальным данным максимальное давление в конце сгорания достигается при угле поворота коленчатого вала после ВМТ, равному по абсолютной величине углу начала видимого сгорания – φс¢ (момент отрыва линии давлений от сгорания над линией давлений от сжатия). Поэтому можно принять рz при φ=360+ φс¢. Для двигателя с искровым зажиганием это давление равно действительному давлению, уточненному при скруглении индикаторной диаграммы в тепловом расчете. Для дизельного двигателя максимальное давление сгорания равно расчетному значению.
На участке расширения от φ=360+ φс¢ до момента открытия выпускного клапана (точка в¢ на индикаторной диаграмме), расчет текущих давлений выполняется по аналогии с расчетом в процессе сжатия по формуле
 , (2.6)
, (2.6)
где 
 – расчетное давление в конце расширения, принимается из теплового расчета.
– расчетное давление в конце расширения, принимается из теплового расчета.
Давление в момент открытия выпускного клапана определяется по формуле (2.6) при подстановке угла jв¢=180-φвып=540-φвып аналогично определению этого давления в тепловом расчете при скруглении индикаторной диаграммы.
Давление в конце расширения при j=540 °ПКВ (на индикаторной диаграмме точка – в¢¢). принимается равным среднему значению между расчетным рb и начальным ра, т. е. рв¢¢=(рb+ ра)/2. Далее от давления рв¢¢ в НМТ до давления рr в ВМТ (j=720 °ПКВ) можно принять уменьшение давлений примерно пропорционально углу φ.
По данным расчета строится действительная (точнее приближенная к действительной диграмме) развернутая индикаторная диаграмма. Эту диаграмму можно строить или в единицах измерения давления, или в единицах измерения силы. Соответственно и остальные силы, действующие в КШМ, определяются в тех же единицах измерения. При переходе от сил к давлениям и обратно делят или умножают соответствующие значения на площадь поршня.
Пример расчета и построения развернутой индикаторной диаграммы в размерности сил (Рг в кН) приведен в Приложении.
Сила инерции возвратно-поступательно движущихся масс определяется по формуле, кН
|
|
|
Рj = - mj×jп,/1000 = -mj×R ×w2 (сosj + lсos2j)/1000, (2.7)
где jп – ускорение поршня в м/с2, принимается из предыдущих расчетов или рассчитывается;
mj – приведенная к оси поршневого пальца масса КШМ, совершающая возвратно-поступательное движение, кг;
R – радиус кривошипа, м;
w – угловая скорость, рад/с.
Приведенная масса mj определяется
mj= mп+mшп, (2.8)
где mп – масса поршневой группы (комплекта), кг;
mшп – масса шатуна, приведенная к оси поршневого пальца, кг.
Приведенная масса составляет mшп=(0,2-0,3)·mш; mш– масса шатуна.
Обычно расчет mj выполняют
mj= mп+0,275·mшп, (2.9)
Массы поршневой группы и шатуна можно определить по статистическим данным конструктивных масс, представляющих отношение массы соответствующего элемента КШМ к площади поршня
m′=m/Fп, (2.10)
Конструктивные массы m′ в зависимости от диаметра поршня (D подставлять в мм) представлены в таблице 1.4.
Таблица1.4
| Тип двигателя | Частота вращения, об/мин | Конструктивная масса m′, кг/м2 | |
| поршневая группа | шатун | ||
| Двигатели с искровым зажиганием | n≤4500 n>4500 | (1,08…1,2)·D (1,2…1,25)·D | (1,35…1,45)·D (1,7…2,0)·D |
| Дизели автомобильные | n≤3000 n>3000 | (1,8…2,0)·D (1,5…1,7)·D | (2,1…2,25)·D (1,6…1,9)·D |
| Дизели тракторные | (2,0…2,2)·D | (2,3…2,5)·D |
Сила инерции возвратно-поступательно движущихся масс так же, как и сосредоточенная сила от давления газов, действует по оси цилиндра. Их равнодействующая (суммарная сила) определяется алгебраическим (с учетом только знаков + и -) суммированием этих двух сил, т.е.
Р∑=Рг+Рj (2.11)
Сила Р∑ действует по оси цилиндра. За положительное направление принято направление в сторону коренной шейки коленчатого вала.
Нормальная сила N (кН), действующая по нормали на стенку цилиндра определяется
N = Р∑ · tgb (2.12)
Сила N считается положительной, если создаваемый ею момент относительно оси коленчатого вала направлен противоположно направлению вращения вала двигателя.
Сила S (кН), действующая вдоль шатуна, определяется
S = Р∑ · (1/ cosb) (2.13)
Она считается положительной, если сжимает шатун, и отрицательной, если растягивает.
Сила К (кН), направленная по радиусу кривошипа
К = Р∑×cos (j + b)/cosb (2.14)
Сила К считается положительной, если она сжимает щеки колена.
Тангенциальная сила Т (кН), направленная по касательной к окружности радиуса кривошипа
Т = Р∑ · sin(j + b)/cosb (2.15)
Сила Т принимается положительной, если направление создаваемого ею момента совпадает с направлением вращения коленчатого вала.
Численные значения тригонометрических функций, входящих в формулы (2.12)…(2.15), приведены в таблицах 1.5 – 1.8.
Таблица 1.5
| j° | Знак | Значения tg b при l | Знак | j° | |||||||
| 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | ||||
| + + + + + + + + + + + + + + + + + + + | 0,042 0,082 0,121 0,156 0,186 0,211 0,230 0,241 0,245 0,241 0,230 0,211 0,186 0,156 0,121 0,082 0,042 | 0,043 0,086 0,126 0,162 0,194 0,220 0,240 0,252 0,256 0,252 0,240 0,220 0,194 0,162 0,126 0,086 0,043 | 0,045 0,089 0,131 0,169 0,202 0,230 0,250 0,263 0,267 0,263 0,250 0,230 0,202 0,169 0,131 0,089 0,045 | 0,047 0,093 0,136 0,176 0,210 0,239 0,260 0,273 0,278 0,273 0,260 0,239 0,210 0,176 0,136 0,093 0,047 | 0,049 0,096 0,141 0,182 0,218 0,248 0,270 0,284 0,289 0,284 0,270 0,248 0,218 0,182 0,141 0,096 0,049 | 0,050 0,100 0,146 0,189 0,226 0,257 0,280 0,295 0,300 0,295 0,280 0,257 0,226 0,189 0,146 0,100 0,050 | 0,052 0,103 0,151 0,196 0,234 0,267 0,291 0,306 0,311 0,306 0,291 0,267 0,234 0,196 0,151 0,103 0,052 | 0,054 0,106 0,156 0,202 0,243 0,276 0,301 0,316 0,322 0,316 0,301 0,276 0,243 0,202 0,156 0,106 0,054 | – – – – – – – – – – – – – – – – – – – |
Таблица 1.6
| j° | Знак | Значения 1 / сosb при l | Знак | j° | |||||||
| 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | ||||
| + + + + + + + + + + + + + + + + + + + | 1,001 1,003 1,007 1,012 1,017 1,022 1,026 1,029 1,030 1,029 1,026 1,022 1,017 1,012 1,007 1,003 1,001 | 1,001 1,004 1,008 1,013 1,019 1,024 1,028 1,031 1,032 1,031 1,028 1,024 1,019 1,013 1,008 1,004 1,001 | 1,001 1,004 1,009 1,014 1,020 1,026 1,031 1,034 1,035 1,034 1,031 1,026 1,020 1,014 1,009 1,004 1,001 | 1,001 1,004 1,009 1,015 1,022 1,028 1,033 1,037 1,038 1,037 1,033 1,028 1,022 1,015 1,009 1,004 1,001 | 1,001 1,005 1,010 1,016 1,024 1,030 1,036 1,040 1,041 1,040 1,036 1,030 1,024 1,016 1,010 1,005 1,001 | 1,001 1,005 1,01 1,018 1,025 1,032 1,039 1,043 1,044 1,043 1,039 1,032 1,025 1,018 1,01 1,005 1,001 | 1,001 1,005 1,01 1,019 1,027 1,035 1,041 1,046 1,047 1,046 1,041 1,035 1,027 1,019 1,01 1,005 1,001 | 1,001 1,006 1,012 1,020 1,029 1,037 1,044 1,049 1,050 1,049 1,044 1,037 1,029 1,020 1,012 1,006 1,001 | + + + + + + + + + + + + + + + + + + + |
Таблица 1.7
| j° | Знак | Значения сos (j+b)/сosb при l | Знак | j° | |||||||
| 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | ||||
| + + + + + + + + – – – – – – – – – – – | 0,978 0,912 0,806 0,666 0,500 0,317 0,126 0,064 0,245 0,411 0,558 0,683 0,785 0,866 0,926 0,968 0,992 | 0,977 0,910 0,803 0,662 0,494 0,309 0,117 0,075 0,256 0,422 0,568 0,691 0,792 0,870 0,929 0,969 0,992 | 0,977 0,909 0,801 0,657 0,488 0,301 0,107 0,085 0,267 0,432 0,577 0,699 0,798 0,875 0,931 0,970 0,993 | 0,977 0,908 0,798 0,653 0,482 0,293 0,098 0,095 0,278 0,443 0,586 0,707 0,804 0,879 0,934 0,971 0,993 | 0,976 0,907 0,795 0,649 0,476 0,285 0,088 0,106 0,289 0,453 0,596 0,715 0,810 0,883 0,937 0,973 0,993 | 0,976 0,906 0,793 0,645 0,469 0,277 0,078 0,117 0,300 0,464 0,606 0,723 0,816 0,887 0,939 0,974 0,994 | 0,975 0,905 0,790 0,640 0,463 0,269 0,069 0,127 0,311 0,475 0,615 0,731 0,822 0,892 0,942 0,975 0,994 | 0,975 0,903 0,788 0,636 0,457 0,261 0,059 0,138 0,322 0,485 0,625 0,739 0,829 0,896 0,944 0,976 0,994 | + + + + + + + + – – – – – – – – – – – |
Таблица 1.8
| j° | Знак | Значения sin (j+b) / сosb при l | Знак | j° | |||||||
| 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | 0,31 | ||||
| + + + + + + + + + + + + + + + + + + + | 0,215 0,419 0,605 0,762 0,886 0,972 1,018 1,027 0,943 0,861 0,760 0,646 0,524 0,395 0,265 0,133 | 0,216 0,423 0,609 0,767 0,891 0,976 1,022 1,029 0,941 0,858 0,756 0,641 0,519 0,391 0,261 0,131 | 0,218 0,426 0,613 0,772 0,896 0,981 1,025 1,030 0,939 0,854 0,751 0,636 0,513 0,387 0,258 0,129 | 0,220 0,429 0,618 0,777 0,901 0,985 1,029 1,032 0,937 0,851 0,747 0,631 0,508 0,382 0,255 0,127 | 0,221 0,432 0,622 0,782 0,906 0,990 1,032 1,034 0,936 0,847 0,742 0,626 0,503 0,378 0,252 0,126 | 0,223 0,436 0,627 0,788 0,912 0,995 1,035 1,036 0,934 0,844 0,737 0,620 0,498 0,373 0,248 0,124 | 0,225 0,439 0,631 0,793 0,917 0,999 1,039 1,038 0,932 0,840 0,733 0,615 0,493 0,369 0,245 0,122 | 0,227 0,442 0,636 0,798 0,922 1,004 1,043 1,040 0,930 0,837 0,728 0,610 0,488 0,364 0,242 0,121 | – – – – – – – – – – – – – – – – – – – |
Расчеты всех сил выполняются в форме таблицы. По расчетным данным строят графики применения сил N, S, R и N в зависимости от угла поворота коленчатого вала j.
Пример расчета сил и их графики приведены в Приложении.
Крутящий момент одного цилиндра Мi ., МН×м:
Мi. = Т×R, (2.16)
Величина и характер изменения тангенциальных сил и крутящих моментов по углу поворота коленчатого вала всех цилиндров двигателя одинаковы и отличаются лишь угловыми интервалами, равными угловым интервалам между рабочими ходами в отдельных цилиндрах. Поэтому для подсчета суммарной тангенциальной силы или суммарного крутящего момента двигателя достаточно иметь данные тангенциальной силы и крутящего момента только одного цилиндра.
Угловой интервал (период изменения) тангенциальной силы и крутящего момента четырехтактного двигателя определяется
q = 720 /i, (2.17)
гдеi – число цилиндров.
Суммирование значений тангенциальных сил и крутящих моментов всех цилиндров двигателя можно выполнить аналитически или графически. По полученным данным строится график тангенциальной силы или крутящего момента всех цилиндров двигателя для углового интервала от j=0 до j=q.
Среднее значение тангенциальной силы или крутящего момента определяется путем алгебраического (с учетом знаков + и -) суммирования площадей, образованных графиком тангенциальной силы (крутящего момента), ординатами крайних точек углового интервала и осью абсцисс и делением этой площади на отрезок абсциссы между крайними точками. Полученное таким образом значение ординаты в масштабе отражает значение средней величины тангенциальной силы или крутящего момента всех цилиндров многоцилиндрового ДВС.
Правильность расчетов проверяется путем сравнения данных теплового расчета
Мср = Мi = Ме /hм, (2.18)
Тср=Ме/(hм·R) (2.19)
и Мср или Тср, полученных по площади из графиков М или Т.
Результаты не должны отличаться между собой более 5 %.
Пример расчета Тср приведен в Приложении.
Уравновешивание и равномерность хода двигателя
В курсовом проекте следует оценить максимальную величину неуравновешенности разрабатываемого двигателя от сил инерции первого и второго порядка и их продольных моментов и показать пути их полного уравновешивания.
Следует определить следующие суммарные значения:
∑РjI=? ∑РjII=? ∑MjI=? ∑MjII=? (3.1)
Центробежные силы от вращающихся масс всегда можно уравновесить с помощью противовесов на продолжении щек кривошипов и поэтому их можно не рассматривать.
В случае выбора конструктивной схемы полностью уравновешенного двигателя значения величин (2.19) равны нулю.
Уравновешенность двигателя зависит от компоновки блока цилиндров двигателя (линейные ПДВС, V-образные и т.д.), числа коленчатых валов (одно- двух- или многовальные ПДВС), расположения кривошипов коленчатого вала (плоские или пространственные коленчатые валы). Ввиду большого конструктивного разнообразия ПДВС анализ уравновешенности двигателей не приводится. Студент выбирает конструкцию ДВС по своему усмотрению и при анализе уравновешенности двигателя должен использовать дополнительную литературу.
Изменение крутящего момента с периодом q = 720 /i оценивается коэффициентом неравномерности крутящего момента
m = (Мmax – Мmin)/Мср, (3.2)
Изменение крутящего момента неизбежно вызывает изменение угловой скорости двигателя – w. Это изменение принято оценивать коэффициентом неравномерности хода двигателя
d= (wmax – wmin)/ wср, (3.3)
Для получения требуемого коэффициента d (d=0,02…0,025 – для динамичных автомобилей; d=0,005…0,01 – для двигателей тракторов и тягачей) в конструкции двигателей предусматривается маховик, в котором сосредотачивается практически весь момент инерции Jм. Увеличением Jм можно получить сколь угодно малую величину d.
Момент инерции маховика определяют исходя из безразмерного момента инерции – Ψ, оцениваемого по формуле
Ψ= Jм·wном2/Мном (3.4)
где wном – скорость двигателя на номинальном режиме;
Мном – крутящий момент двигателя на номинальном режиме.
Для большинства автотракторных двигателей значение Ψ изменяется в пределах Ψ =200…350.
Задавшись значением Ψ, из (3.4) можно определить момент инерции маховика Jм
Jм = Ψ·Мном/wном2, (3.5)
а затем массу маховика mм,
mм, = 4· Jм/Dмср2 (3.6)
где Dмср – средний диаметр маховика.
Для предварительных расчетов можно принять Dмср = (2...3)×S,
где S – ход поршня.
Внешний диаметр маховика Dм выбирается с учетом обеспечения допустимых окружных скоростей.
Допустимая окружная скорость маховика Vм:
– для чугунных маховиков Vм £ 25...30 м/с;
– для стальных маховиков Vм £ 40...45 м/с.
Тогда
Dм £60×Vм /(p × nном), (3.7)
где nном– номинальная частота вращения коленчатого вала.
Внешний диаметр маховика Dм учитываем при разработке чертежей двигателя.
Приложение
Динамический анализ ПДВС
Динамический анализ кривошипно-шатунных механизмов двигателей с искровым зажиганием и дизельных двигателей одинаков. Поэтому ниже приведем пример динамического анализа только для ДсИЗ с центральным КШМ..
Пусть из теплового расчета имеем: р0=0,1 МПа; ра=0,086 МПа; рс=1,58 МПа;
рz =5,97 МПа; рzд=5,07 МПа; рr=0,11 МПа; n1=1,37; n2=1,27; рb=0,40 МПа;
Vh=0,45 дм3= 450 см3; Vc=60,8 см3; Vа=510,8 см3; λ=0,26. Число цилиндров двигателя i=6. Действительное давление в конце сжатия рс״≈1,2·1,58 =1,90 МПа. Диаметр цилиндра D=84 мм, ход поршня S=82 мм (уточненный рабочий объем цилиндра –484 см3). Площадь поршня Fп=0,00554 м2.
Начало основной фазы сгорания (точка с¢) φс¢ =25 °ПКВ до ВМТ, угол открытия выпускного клапана до НМТ φвып=60 °ПКВ.
Степень сжатия ε=8.4. Частота вращения n=5400 об/мин; ω=π·n/30=3,14·5400/30=565,2 рад/с.
Радиус кривошипа R=S/2=82/2=41 мм.
Определим силу давления газов, используя формулы (2.1), (2.2), (2.5) и (2.6).
В ВМТ при φ=0° давление газов равно рг=рr=0.11 МПа. От φ=30° до φ=180° давление газов равно рг= ра=0,086 МПа. При φ=360° рг= рс״=1,90 МПа. Принимаем максимум давления при 15 °ПКВ после ВМТ, т.е. при φ=375°.
Действительное давление в конце расширения определим как среднее арифметическое между рb=0,40 МПа и ра=0,086 МПа. рb״=(0,40+0,086)/2=0,243 МПа.
При углах от φ=210° до φ=330° давление рассчитываем по формуле (2.5)
В процессе расширения от φ=390° до φ=(540°-φвып) расчет давления выполняем по формуле (2.6). Действительное давление на участке расширения от φвып до НМТ (φ=540°) определяем методом линейной интерполяции (снижение давления по прямой зависимости). Давление на линии выпуска (выталкивания) газов так же находим методом линейной интерполяции между давлениями рb״=0,243 МПа и рr=0.11 МПа. Снижение давления на каждые 30 °ПКВ составит ∆р=(0,243-0,11)/6≈0,022 МПа.
Конструктивная масса поршневой группы для двигателя с искровым зажиганием и n>4500 об/мин m′=(1,2…1,25)D=(1,2…1,25)·84=100,8…105 кг/м2.
Масса поршневой группы равеа
mп= m′· Fп=(100,8…105)·0,00554=0,558…0,582 кг. Примем mп=0,57 кг.
Конструктивная масса шатунной группы для двигателя с искровым зажиганием и n>4500 об/мин m′=(1,7…2,0)D=(1,7…2,0)·84=142,8…168 кг/м2.
Масса шатунной группы равеа
mп= m′· Fп=(142,8…168)·0,00554=0,791…0,931 кг. Примем mп=0,90 кг.
Приведенная к оси поршневого пальца масса инерции по (2.9)
mj= 0,57+0,275·0,9 =0,82 кг.
Для удобства расчета в табличной форме определим величину mj·R·ω2/1000= 0,82·0,041·565,22/1000=10,73994.
Расчеты выполнены в таблице П1
Таблица П1
| φ, °ПКВ | 1-cоsφ+λ·(1- cоs2φ)/4 | рг, МПа | рг- р0, МПа | Рг, кН | cоsφ+λ· cоs2φ | Рj, кН | Р∑, кН |
| 0,11 | 0,01 | 0,055 | 1,2600 | -13,532 | -13,477 | ||
| 0,1665 | 0,086 | -0,014 | -0,078 | 0,9960 | -10,697 | -10,775 | |
| 0,5975 | 0,086 | -0,014 | -0,078 | 0,3700 | -3,974 | -4,052 | |
| 1,13 | 0,086 | -0,014 | -0,078 | -0,2600 | 2,792 | 2,714 | |
| 1,5975 | 0,086 | -0,014 | -0,078 | -0,6300 | 6,766 | 6,688 | |
| 1,8985 | 0,086 | -0,014 | -0,078 | -0,7360 | 7,925 | 7,847 | |
| 0,086 | -0,014 | -0,078 | -0,7400 | 7,948 | 7,870 | ||
| 1,8975 | 0,092 | -0,008 | -0,044 | -0,736 | 7,925 | 7,881 | |
| 1,5975 | 0,112 | 0,012 | 0,067 | -0,6300 | 6,866 | 6,933 | |
| 1,13 | 0,167 | 0,067 | 0,371 | -0,26 | 2,792 | 3,163 | |
| 0,5975 | 0,321 | 0,221 | 1,224 | 0,3700 | -3,974 | -2,750 | |
| 0,1665 | 0,823 | 0,723 | 4,005 | 0,9960 | -10,697 | -6,692 | |
| 1,90 | 1,8 | 9,972 | 1,2600 | -13,532 | -3,560 | ||
| 0,0096 | 5,07 | 4,97 | 27,534 | 1,1840 | -12,716 | 14,818 | |
| 0,1665 | 3,245 | 3,145 | 17,423 | 0,9960 | -10,697 | 6,726 | |
| 0,5975 | 1,357 | 1,257 | 6,964 | 0,3700 | -3,974 | 2,990 | |
| 1,13 | 0,739 | 0,639 | 3,540 | -0,2600 | 2,792 | 6,332 | |
| 1,5975 | 0,513 | 0,413 | 2,288 | -0,6300 | 6,866 | 9,154 | |
| 1,8985 | 0,378* | 0,278 | 1,540 | -0,7360 | 7,925 | 9,465 | |
| 0,243 | 0,143 | 0,792 | -0,7400 | 7,948 | 8,740 | ||
| 1,895 | 0,221 | 0,121 | 0,670 | -0,736 | 7,925 | 8,595 | |
| 1,5975 | 0,199 | 0,099 | 0,548 | -0,6300 | 6,766 | 7,314 | |
| 1,13 | 0,177 | 0,077 | 0,427 | -0,26 | 2,792 | 3,219 | |
| 0,5975 | 0,155 | 0,055 | 0,305 | 0,3700 | -3,974 | -3,669 | |
| 0,1665 | 0,133 | 0,033 | 0,183 | 0,9960 | -10,697 | -10,514 | |
| 0,11 | 0,01 | 0,055 | 1,2600 | -13,532 | -13,477 |
*определено так (0,243+0,513)/2=0,378.
В таблице П2 выполнены расчеты сил, действующих в КШМ, по формулам (2.12) – (2.15) и крутящего момента одного цилиндра ДВС по (2.16).
Таблица П2
| φ, °ПКВ | Р∑, кН | 
| N, кН | 
| S, кН | 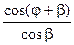
| К, кН | 
| Т, кН | М Н·м |
| -13,477 | -13,477 | -13,477 | ||||||||
| -10,775 | 0,131 | -1,412 | 1,009 | -10,872 | 0,801 | -8,631 | 0,613 | -6,605 | -271 | |
| -4,052 | 0,230 | -0,932 | 1,026 | -4,157 | 0,301 | -1,220 | 0,981 | -3,975 | -163 | |
| 2,714 | 0,267 | 0,725 | 1,035 | 2,809 | -0,267 | -0,725 | 2,714 | |||
| 6,688 | 0,230 | 1,538 | 1,026 | 6,862 | -0,699 | -4,675 | 0,751 | 5,023 | ||
| 7,847 | 0,131 | 1,028 | 1,009 | 7,918 | -0,931 | -4,676 | 0,387 | 3,037 | ||
| 7,870 | 7,870 | -1 | -7,870 | |||||||
| 7,881 | -0,131 | -1,032 | 1,009 | 7,952 | -0,931 | -7,337 | -0,387 | -3,050 | -125 | |
| 6,933 | -0,230 | -1,595 | 1,026 | 7,113 | -0,699 | -4,846 | -0,751 | -5,207 | -213 | |
| 3,163 | -0,267 | -0,845 | 1,035 | 3,274 | -0,267 | -0,845 | -1 | -3,163 | -130 | |
| -2,750 | -0,230 | 0,633 | 1,026 | -2,822 | 0,301 | -0,828 | -0,981 | 2,698 | ||
| -6,692 | -0,131 | 0,877 | 1,009 | -6,752 | 0,801 | -5,360 | -0,613 | 4,102 | ||
| -3,560 | -3,560 | -3,56 | ||||||||
| 14,818 | 0,067 | 0,993 | 1,003 | 14,862 | 0,943 | 13,973 | 0,322 | 4,771 | ||
| 6,726 | 0,131 | 0,881 | 1,009 | 6,787 | 0,801 | 5,388 | 0,613 | 4,123 | ||
| 2,990 | 0,230 | 0,688 | 1,026 | 3,068 | 0,301 | 0,900 | 0,981 | 2,933 | ||
| 6,332 | 0,267 | 1,691 | 1,035 | 6,554 | -0,267 | -1,691 | 6,332 | |||
| 9,154 | 0,230 | 2,105 | 1,026 | 9,392 | -0,699 | -6,399 | 0,751 | 6,875 | ||
| 9,465 | 0,131 | 1,240 | 1,009 | 9,550 | -0,931 | -8,812 | 0,387 | 3,663 | ||
| 8,740 | 8,740 | -1 | -8,740 | |||||||
| 8,595 | -0,131 | -1,126 | 1,009 | 8,672 | -0,931 | |||||
|
|
|


