Квантово-механическая модель строения атома

Модели строения атома

Модель Томсона

Первая модель строения атома была предложена Дж. Томсоном в 1904 г.,

согласно которой атом – положительно заряженная сфера с вкрапленными в нее электронами. Несмотря на свое несовершенство томсоновская модель

позволяла объяснить явления испускания, поглощения и рассеяния света атомами, а также установить число электронов в атомах легких элементов.

Модель Резерфорда

Модель Томсона была опровергнута Э. Резерфордом (1911 г.), который доказал, что положительный заряд и практически вся масса атома сконцентрированы в малой части его объема – ядре, вокруг которого двигаются электроны. Эта модель строения атома известна как планетарная,

т. к. электроны вращаются вокруг ядра подобно планетам солнечной системы.

Согласно законам классической электродинамики, движение электрона по окружности вокруг ядра будет устойчивым, если сила кулоновского притяжения будет равна центробежной силе. Однако, в соответствии с теорией электромагнитного поля, электроны в этом случае должны двигаться по спирали, непрерывно излучая энергию, и падать на ядро. Однако атом устойчив.

К тому же при непрерывном излучении энергии у атома должен наблюдаться непрерывный, сплошной спектр. На самом деле спектр атома состоит из отдельных линий и серий.

Таким образом, данная модель противоречит законам электродинамики и не объясняет линейчатого характера атомного спектра.

 

Модель Бора

В 1913 г. Н. Бор предложил свою теорию строения атома, не отрицая при этом полностью предыдущие представления. В основу своей теории Бор положил два постулата.

Первый постулат говорит о том, что электрон может вращаться вокруг ядра только по определенным стационарным орбитам. Находясь на них, он не излучает и не поглощает энергию. При движении по любой стационарной орбите запас энергии электрона (Е_1, Е₂ …) остается постоянным. Чем ближе к ядру расположена орбита, тем меньше запас энергии электрона Е₁ ˂ Е₂ …˂ Е_n.

Энергия электрона на орбитах определяется уравнением:

 

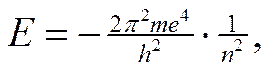
где m – масса электрона, h – постоянная Планка, n – 1, 2, 3… (n=1 для 1-ой орбиты, n=2 для 2-ой и т.д.).

Второй постулат говорит о том, что при переходе с одной орбиты на другую электрон поглощает или выделяет квант (порцию) энергии.

Если подвергнуть атомы воздействию (нагреванию, облучению и др.), то электрон может поглотить квант энергии и перейти на более удаленную от ядра орбиту. В этом случае говорят о возбужденном состоянии атома. При обратом переходе электрона (на более близкую к ядру орбиту) энергия выделяется в виде кванта лучистой энергии – фотона. В спектре это фиксируется определенной линией. На основании формулы

,

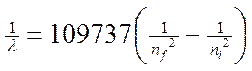где λ – длина волны, n = квантовые числа, характеризующие ближнюю и дальнюю орбиты, Бор рассчитал длины волн для всех серий в спектре атома водорода. Полученные результаты соответствовали экспериментальным данным. Стало ясным происхождение прерывистых линейчатых спектров. Они – результат излучения энергии атомами при переходе электронов из возбужденного состояния в стационарное. Переходы электронов на 1-ю орбиту образуют группу частот серии Лаймана, на 2-ю – серию Бальмера, на 3-ю серию Пашена (табл. 1).

Таблица 1

Проверка формулы Бора для серий водородного спектра

Название серии	λ, А Экспериментальная	λ, А Вычисленная Бором
Пашена	18751,3 12817,5 10938,0 10049,8
Бальмера	6564,66 4862,71 4102,91 3971,20 3799,00 3712,70	6564,70 4862,80 4341,70 4102,93 3971,23 3799,01 3712,62
Лаймана		1215,68 1025,73 972,5

 

Однако, теория Бора не смогла объяснить расщепление линий в спектрах многоэлектронных атомов. Бор исходил из того, что электрон – это частица, и использовал для описания электрона законы, характерные для частиц. Вместе с тем накапливались факты, свидетельствующие о том, что электрон способен проявлять и волновые свойства. Классическая механика оказалась не в состоянии объяснить движение микрообъектов, обладающих одновременно свойствами материальных частиц и свойствами волны. Эту задачу позволила решить квантовая механика – физическая теория, исследующая общие закономерности движения и взаимодействия микрочастиц, обладающих очень малой массой (табл. 2).

Таблица 2

Свойства элементарных частиц, образующих атом

Частица	Заряд	Масса
Кл	Условн.ед.	г	А.е.м.
Электрон	- 1,6·10-19	-1	9,10·10-28	0,00055
Протон	1,6·10-19	+1	1,67·10-24	1,00728
Нейтрон			1,67·10-24	1,00866

 

Квантово-механическая модель строения атома

В основе современной теории строения атома лежат следующие основные положения:

1. ЭЛЕКТРОН ИМЕЕТ ДВОЙСТВЕНУЮ (корпускулярно-волновую) ПРИРОДУ.

Электрон, как и другие элементарные частицы (протон, нейтрон), обладает определенной массой и зарядом, т.е. ведет себя как частица. В то же время, движущийся электрон проявляет волновые свойства, например характеризуется способностью к дифракции (рассеяние световых лучей) и интерференции (наложение световых волн). Для любой элементарной частицы справедливо уравнение (Луи де Бройль), связывающее параметры волны и частицы

,

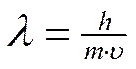где λ – длина волны электрона, h - постоянная Планка, m – масса электрона,

υ – скорость движения электрона.

2. ДЛЯ ЭЛЕКТРОНА НЕВОЗМОЖНО ОДНОВРЕМЕННО ТОЧНО ИЗМЕРИТЬ КООРДИНАТУ И СКОРОСТЬ.

В силу наличия у микрочастиц волновых свойств невозможно в каждый момент времени точно фиксировать их положение в пространстве и определять

с любой точностью скорость их движения. Чем точнее мы измеряем один параметр, тем больше неопределенность в другом. Принцип неопределенности сформулирован Гейзенбергом (1927 г.) и имеет математическое выражение

,

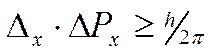где Δ_х – неопределенность положения частицы по оси х, ΔР_х = Δ(m·υ) – неопределенность составляющей импульса по оси х.

Из формулы видно, что чем меньше значение Δ_х , т.е. чем определеннее положение частицы, тем больше ΔР_х, т.е. тем неопределеннее ее импульс. Неопределенность в свойствах микрообъектов проявляется тем в большей степени, чем в большей степени выражена его волновая функция (чем меньше его масса). Поэтому неопределенность в положении электрона значительно больше, чем неопределенность в положении ядра атома.

2. ЭЛЕКТРОН В АТОМЕ НЕ ДВИЖЕТСЯ ПО ОПРЕДЕЛЕННЫМ

ТРАЕКТОРИЯМ, А МОЖЕТ НАХОДИТСЯ В ЛЮБОЙ ЧАСТИ ОКОЛОЯДЕРНОГО ПРОСТРАНСТВА, однако вероятность его нахождения в разных частях этого пространства неодинакова.

Вероятность нахождения электрона в разных местах околоядерного пространства можно определить с помощью уравнения Шредингера

,

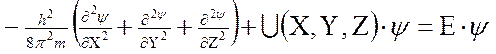где h – постоянная Планка, m – масса электрона, U – потенциальная энергия,

Е – полная энергия, ψ – волновая (пси) функция. Первый член уравнения

соответствует кинетической энергии частицы (Е_к) с массой m. При короткой записи Е_к описывается оператором Лапласа

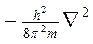
где - оператор Лапласа.

Упрощенный вид уравнения Шредингера

.

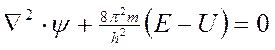Решение этого уравнения связано с большими математическими трудностями. Точное решение оно имеет для атома водорода и для одноэлектронных частиц. Для сложных атомов уравнение Шредингера может быть решено только приблизительно. Решая его находят энергию электрона, а также функцию координат электрона X, Y, Z и времени τ: 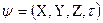. Волновая функция ψ представляет собой амплитуду трехмерной электронной волны. Причем она имеет как положительные, так и отрицательные значения. Квадрат модуля волновой функции 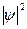характеризует вероятность нахождения электрона в некотором объеме. Эту величину называют также электронной плотностью. Если в соответствии с Ур авнением Шредингера получим, что , где - определенный объем, то это значит, что в данном объеме электрон находится 0,1 времени, а 0,9 – в другом месте, т.е. можно утверждать, что электронная плотность в данном объеме равна 0,1. Совокупность мест пространства, где 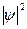имеет максимальное значение называют электронной орбиталью.

Таким образом, электронной орбиталью или электронным облаком называется часть околоядерного пространства, в котором вероятность пребывания электрона максимальна.

Поверхность, охватывающая ядро атома, за пределами которой вероятность пребывания электрона исчезающее мала, называют граничной поверхностью орбитали, которая и передает форму самой орбитали.

4. ЯДРА АТОМОВ СОСТОЯТ ИЗ ПРОТОНОВ И НЕЙТРОНОВ

(общее название - нуклоны).

Число протонов в ядре равно порядковому номеру элемента в таблице Д.И. Менделеева, а сумма протонов и нейтронов его атомному числу. Массовое число (А), заряд ядра (Z), равный числу протонов, и число нейтронов (N)

связаны соотношениями: Z = А – N, N = А – Z, А = Z + N.

Атомы с одинаковыми Z, но разными А и N, называют изотопами.

 

Квантовые числа

Решение уравнения Шредингера позволяет найти волновые функции, при этом выяснено, что для полного определения каждого решения необходимы три целых числа – квантовые числа. Можно сказать, что квантовые числа описывают совокупность движений электронов в атоме.

ГЛАВНОЕ КВАНТОВОЕ ЧИСЛО (n) определяет общую энергию электрона на данной орбитали и принимает значения n = 1, 2, 3, 4….

Чем больше n, тем больше объем внутреннего пространства атомной орбитали, т.е. растет удаленность электрона от ядра атома. Все электроны с одинаковым значением главного квантового числа образуют электронный слой. Приняты следующие обозначения электронных слоев:

Значение n ……………………………. 1 2 3 4 5 6 7

Обозначение слоя (уровня) ………….. K L M N O P Q.

Зная главное квантовое число можно определить максимальное число электронов, которое может находиться на этом уровне по формуле N_е = 2n².

Возможное число подуровней для каждого электронного уровня численно равно значению n– первый уровень (n = 1) состоит из одного подуровня, второй уровень (n = 2) – из двух и т.д. (табл.3).

ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО (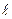), которое иногда называют побочным квантовым числом, определяет форму электронного облака и принимает значения от нуля до n-1. Область электронного уровня, в котором содержатся орбитали определенной формы называется энергетическим подуровнем. Подуровень, содержащий s-орбитали, называется s-подуровнем,

р-орбитали - р-подуровнем и т.д. Например, при n = 1, 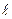= 0 (на первом уровне существуют только s-электроны). При n = 3, 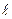= 0, 1, 2 (на третьем уровне содержит 3s-, 3р- и 3d-электроны).

Таблица 3

Максимальное число подуровней и орбиталей на энергетических уровнях

 

Энергетический уровень	Число подуровней	Типы орбиталей	Орбитали,
К (n = 1)		1s
L (n = 2)		2s 2p	-1, 0, +1
M (n = 3)		3s 3p 3d	-1, 0, +1 -2, -1, 0, +1, +2
N (n = 4)		4s 4p 4d 4f	-1, 0, +1 -2, -1, 0, +1, +2 -3, -2, -1, 0, +1, +2, +3

 

Если 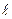= 0, электронное облако имеет сферическую форму;

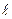= 1 - электронное облако имеет форму симметричной восьмерки (гантель).

С ростом численного значения орбитального квантового числа форма электронного облака усложняется.

МАГНИТНОЕ КВАНТОВОЕ ЧИСЛО характеризует ориентацию данной орбитали в пространстве. Магнитное квантовое число принимает целочисленные значения от - 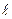до + 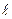, включая ноль. Например, для 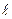= 2, магнитные квантовые числа имеют значения -2, -1, 0, +1, +2, т.е. в данной подоболочке (d-подуровень) существует пять орбиталей. Соответственно на

s-подуровне (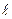 = 0) имеется одна орбиталь; на р-подуровне ( 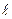= 1) – три орбитали; на f-подуровне – семь орбиталей. Атомную орбиталь обозначают в виде клеточки □. Тогда число орбиталей на соответствующих подуровнях будет равно: s-подуровень - □; р-подуровнь - □□□; d-подуровень - □□□□□;

f-подуровнь - □□□□□□□.

Вышерассмотренные квантовые числа полностью характеризуют три определяющих свойства электрона-волны: длину, направление и амплитуду. Однако у электрона-частицы имеется особое свойство, называемое спином. Упрощенно спин можно рассматривать как вращение электрона вокруг собственной оси. Поэтому в теорию строения атома введено еще одно

СПИНОВОЕ КВАНТОВОЕ ЧИСЛО (m_s), которое может принимать два значения в соответствии с двумя возможными направлениями вращения:

m_s = + ½ (электрон вращается по часовой стрелке вокруг своей оси и имеет обозначение), m_s = - ½ (электрон вращается против часовой стрелки вокруг своей оси и имеет обозначение).

 

Многоэлектронные атомы

В многоэлектронном атоме на электрон действует не только сила притяжения со стороны положительного заряженного ядра, но и отталкивание со стороны других электронов. Электроны внутренних электронных уровней атома ослабляют притяжение внешнего электрона ядром – экранируют внешний электрон от ядра. Это экранирование оказывается различным для электронов с разной формой электронного облака. Поэтому в многоэлектронных атомах энергия электрона зависит не только от главного квантового числа, но и от орбитального квантового числа, которое определяет форму электронной орбитали.

Распределение электронов в атоме по уровням и орбиталям происходит в соответствии с принципами Паули, Хунда, наименьших энергий.

Принцип Паули

Принцип (запрет) Паули гласит: в атоме не может быть двух электронов, имеющих одинаковыезначения всех четырех квантовых чисел. Отсюда следует, что на каждой орбитали может быть не более двух электронов, причем они должны иметь антипараллельные спины.

Правило Гунда

В соответствии с этим правилом заполнение орбиталей данного подуровня происходит таким образом, чтобы достигалось максимальное значение суммарного спинового числа (∑m_s).

Поделиться:

Воспользуйтесь поиском по сайту: