Научная деятельность Петровского

Реферат

По спецкурсу “ Математики – политические и государственные деятели России XVIII-XX вв.”

Математик И.Г. Петровский (1901-1973) – ректор Московского государственного университета им. М.В. Ломоносова.

 

 

Выполнил:

Непомнящий Алексей Сергеевич

группа М-23

Проверил:

к.и.н, доцент кафедры истории

Прядко Иван Андреевич

Красноярск

1998

 

Иван Георгиевич Петровский

5(18) января 1901 - 15 января 1973

Ректор Московского университета: 1951 г. – 1973

Декан механико-математического факультета МГУ: 1939 г. - 1944 г.

 

 

План

Введение___________________________________________________________________ 4

Студенческие годы__________________________________________________________ 5

Научная деятельность Петровского___________________________________________ 6

Педагогическая и общественная деятельность________________________________ 10

Работа на посту ректора МГУ______________________________________________ 13

Отзывы коллег_____________________________________________________________ 15

Заключение________________________________________________________________ 17

Используемые источники___________________________________________________ 19

 

Введение

В данном реферате мной делается попытка рассказать об одном из известнейших и талантливейших математиков XX века – Иване Георгиевиче Петровском. Я хочу осветить не только его поистине грандиозную научную деятельность, ведь Петровский – автор современной теории дифференциальных уравнений, автор многих научных работ по другим областям математики, которые пользуются авторитетом в научной среде, но и как о талантливом организаторе и общественном деятеле. Петровский с 1951-го года и до самой своей смерти в 1973-м году был ректором Московского Государственного Университета, под его руководством в МГУ начали работать десятки новых кафедр, новые факультеты. Также Петровский был замечательным педагогом и оставил после себя великолепные книги по курсам, прочитанным им на механико-математическом факультете МГУ. Исследовать жизнь и деятельность этого поистине гениального человека я и пытаюсь.

Студенческие годы

Иван Георгиевич Петровский родился 5-го января (18-го по новому стилю) 1901-го года в г. Севске Орловской губернии в купеческой семье. Дата рождения Ивана Георгиевича приводится по его автобиографии (архив отдела редких книг НБ МГУ, Ф.22, оп.1, ед.хр.65, л.5). Интересно, что в сохранившейся метрике указывается другая дата - 6 января 1901 г. (архив МГУ, Ф.260, оп.1, д.1, л.1). Городское реальное училище он окончил в 1917-м году с отличными отметками по всем дисциплинам, кроме двух: математики и рисования. Но (парадоксы педагогики!) рисовать он любил, любовь к искусству, живописи (среди особо любимых им художников можно назвать Рембрандта, Серова, Нестерова и других) станет в дальнейшем неотъемлемой частью его всесторонне развитой одаренной натуры, а его фундаментальные труды в области математики вообще, и в области построения общей теории обыкновенных дифференциальных уравнений в частности, во многом и надолго определят характер ряда направлений современной науки. Окончив училище, Петровский едет в Москву в надежде поступить в Московский университет. Сначала он поступает на естественное отделение физико-математического факультета Московского университета, но вскоре оставляет его и возвращается в семью, переехавшую к этому времени в Елизаветград. Здесь он учится в Механико-машиностроительном институте, где проявился его интерес к математике. Как пишет сам Петровский в автобиографии, первой его математической книгой была “Теория чисел” немецкого ученого Петера Густава Дирихле. Эта книга так поразила его красотой мыслей и фактов, что навсегда повернула его в сторону математики. Также немалое влияние на Петровского произвела и книга Николая Егоровича Жуковского по теоретической механике. Вернувшись в университет в 1922-м году, он определяется на математическое отделение физико-математического факультета.

В 1927-м году студент пятого курса Иван Петровский принял участие в первом Всероссийском съезде математиков, выступив с приветственной речью от имени молодежи физико-математического факультета МГУ.

Петровский в свои студенческие годы, пришедшиеся на послевоенные, голодные для России годы, имел мало условий для учебы. Ему приходилось днем зарабатывать деньги на жизнь и вечерами учиться самостоятельно по книгам. Ему пришлось сменить множество профессий: он был и дворником, и грузчиком, и учителем. Так, с 1923-го по 1930-й год он работал преподавателем математики на рабфаке Высших художественно-творческих мастерских (ВХУТЕМАС), и с некоторыми из своих учеников, ставших впоследствии скульпторами, художниками, музыкантами, он сохранил дружеские отношения и в будущем.

Научная деятельность Петровского

Большое влияние на молодого Петровского оказал профессор Дмитрий Федорович Егоров, аспирантом которого он был в 1927-1930-х годах. Егоров занимался задачами в области дифференциальной геометрии, теории интегральных уравнений, теории функций и других областях прикладного математического анализа. Таким образом, род будущих исследований самого Петровского был предопределен в это время. Его первая научная работа была посвящена исследованию задачи Дирихле об отыскании гармонической функции, задаваемой уравнением (частный вид уравнения Лапласа на плоскости), имеющей большое значение в прикладных задачах механики. Петровским в 1928-м году впервые была доказана общая теорема единственности решения этой задачи. Позже, в 1941-м году, Петровским была решена более общая задача Дирихле для уравнений Лапласа. С тех лет, проведенных в аспирантуре под началом Егорова, большинство работ Петровский посвятил исследованиям дифференциальных уравнений. Но вообще Петровский никогда не замыкался на исследовании какой-либо отдельной области математики. Напротив, он старался интегрировать различные разделы математики, применял методы, характерные для одного из разделов к другому. 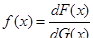Так, Петровскому принадлежит полное решение задачи об определении примитивной F(x) по значению производной относительно заданной G(x), настойчиво выдвигавшейся академиком Н. Н. Лузиным в конце двадцатых годов. Выработанные при решении этой задачи методы Петровский применил к решению задач теории вероятности. Этот метод описан в книге А. И. Хинчина “Асимптотические законы теории вероятности”.

Тридцатые годы для Ивана Георгиевича были наполнены наиболее интенсивной и напряженной творческой и научной работой пожалуй, за всю его жизнь. С 1929-го года Петровский начинает преподавать в МГУ. Он не только читал курсы по дифференциальным уравнениям, интегральным уравнениям и другие, но также организовывал и участвовал в работе научных семинаров, посвященных разным проблемам прикладной математики.

В тридцатые годы Петровским получены фундаментальные результаты в различных областях математики: в алгебраической геометрии, теории вероятностей, теории обыкновенных дифференциальных уравнений, математической физике, теории уравнений с частными производными.

В 1933-м году опубликована первая работа Петровского в области алгебраической геометрии – “Вопросы о топологической природе алгебраических кривых и поверхностей в действительной области”. До Петровского этим вопросом занимался немецкий математик Д. Гильберт, но не смог достичь в этой области существенных результатов ввиду очень большой сложности темы. Замечательные результаты изучения этого вопроса описаны Петровским в 1938-м году, позже он вернулся к этой теме в сотрудничестве с О. А. Олейник и опубликовал результаты в 1949-м году.

В отличие от этой работы, которая носила характер пионерского исследования, его статья о поведении интегральной кривой, задаваемой системой уравнений в окрестности особой точки осталась без продолжения, так как тема была исчерпывающе разработана.

С 1936-го года Петровский работает над задачей Коши и по вопросу об аналитичности решений для системы уравнений в частных производных. Эти работы принесли Петровскому наибольшую известность и были удостоены Государственной премии, поэтому мы рассмотрим их чуть подробнее.

Эти работы сделали решительный шаг в построении новой теории дифференциальных уравнений в частных производных. Фактически, Петровским была построена новая теория со своей классификацией, методами, определениями. Основным направлением в изучении теории дифференциальных уравнениях в частных производных с середины XIX века являлось изучение их с точки зрения существования аналитических функций. Центральное место здесь заняли теоремы, доказанные Софьей Васильевной Ковалевской. При всей значимости и общности результатов этого направления они были оторваны от соответствующих практических задач, были чисто теоретическими, так как гипотеза аналитичности решений и начальных условий оказывалась часто плохой идеализацией действительности.

В конце XIX-го - начале XX-го веков это классическое направление было почти вытеснено противоположным: стали изучаться уравнения математической физики, то есть специальные краевые задачи, подсказанные физикой и механикой непрерывных сред при помощи аппарата, также заимствованного из физики, то есть рассмотрение волн, колебаний и прочего. Но и этот подход не удовлетворял задаче общего развития, требуя перехода к третьему этапу: общему и систематическому изучению систем дифференциальных уравнений с точки зрения тех специальных их свойств, которые выявляются при решении отдельной краевой задачи математической физики, то есть выяснению того, какие краевые задачи “свойственны” данной системе уравнений. В этом направлении до Петровского был высказан ряд общих соображений и получен ряд ценных результатов, но именно работы Петровского показали, что в этом направлении можно продвинуться так далеко, что уже вырисовываются контуры будущей общей теории дифференциальных уравнений, улавливаются все те их существенные черты, которые определяют их естественно - научное применение, и в то же время свободны от исследований второго периода, когда создается такое положение, что теория дифференциальных уравнений в частных производных сводится к коллекции отдельных специальных задач.

Петровский    выделил и изучил классы эллиптических, гиперболических и параболических систем уравнений с частными производными, изучил задачи с начальными условиями для параболических и гиперболических систем в 1936-м году, установил аналитичность решений эллиптических систем в 1937-м году. Работы Петровского, созданные в это время, актуальны и поныне. Специалисты отмечают, что “несмотря на “чисто математический” характер основных работ Петровского, в них по существу проявляется его взгляд на математику как на неотъемлемую часть естествознания, на которой основываются вывод и понимание количественных и качественных закономерностей, составляющих содержание наук о природе”.

К основным исследованиям по условиям существованию и корректности задачи Коши в 1943-1945-х годах Петровский присоединил глубокие исследования о зависимости решения от начальных данных. Иногда этот вопрос называют задачей о лакунах. Этот метод, хотя и созданный Петровским в ходе теоретических изысканий, получил широкое практическое применение. Пользуясь своими открытиями, Петровский сам решал специальные задачи математической физики, как, например, задача о распространении волн Рэлея.

12	Поделиться:

Воспользуйтесь поиском по сайту: