Тема 2. Численное интегрирование. Решение обыкновенных дифференциальных уравнений.

Методические указания и задания к контрольной работе.

А) Каждый студент вначале должен решить контрольные задания, для чего определить параметр своего контрольного задания: S = (N+1), где N – значение последней цифры зачетки.Решение задач должно быть оформлено аккуратно и содержать все промежуточные расчеты. Оформляется произвольным образом. Образцы решений приведены ниже.

Задания:

1. Методом Ньютона или хорд найти корень уравнения x³ +2x – 13 -5+s =0 с точностью e = 10^-3.

i
xi
yi	–1+s	1+s	2+s	4+s	6+s

 

2. Построить по методу наименьших квадратов многочлен первой степени и оценить степень приближения. Значения y_i в точках x_i, i =0, 1, 2, 3, 4 приведены в таблице.

3. Вычислить приближенно по формуле левых, правых или средних прямоугольников (по желанию) интеграл с шагом h =0,1.

Б) Ответить на т еоретические вопросы:

. Вариант первой темы выбирается по последней цифре зачетки, а второй по предпоследней цифре.

Тема 1. Понятие погрешности. Решение уравнений

1. Понятие численных методов.

2. Классификация нелинейных уравнений.

3. Исследование уравнений и отделение корней.

4. Методы решения. Понятие итерации.

5. Источники погрешности решения задач на ЭВМ.

6. Дать описание алгоритма метода половинного деления.

7. Необходимые условия сходимости метода половинного деления.

8. Условие окончания счета метода простой итерации. Погрешность метода.

9. Описание алгоритма метода хорд. Графическое представление метода. Вычисление погрешности.

0. Описание алгоритма метода касательных (Ньютона). Графическое представление метода. Условие выбора начальной точки.

Тема 2. Численное интегрирование. Решение обыкновенных дифференциальных уравнений.

1. Постановка задачи численного интегрирования

2. Метод средних прямоугольников

3. Метод трапеций

4 Метод Симпсона (метод парабол)

5 Правило Рунге практической оценки погрешности

7. Опишите решение задачи Коши методом Эйлера.

8. Опишите решение задачи Коши модифицированным методом Эйлера.

9 Опишите решение задачи Коши методом Рунге-Кутта.

0. Что такое порядок точности метода и как он связан с его эффективностью? Приведите примеры методов разных порядков.

Задача 1. Решение нелинейных уравнений.

Используется итерационные процедуры, которые предполагают:

а) задание начального приближения Хо.

б) использование рекуррентных формул

метод Ньютона 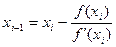или метод хорд где

i=1,2,….до сходимости.

в) критерий остановки дальнейших вычислений по достижении заданной точности:

или , где έ – заданная точность.

Пример решения: решить уравнение х³ – 7 = 0.

1. Находим интервал изоляции корня. Он расположен на отрезке [1,3]. На концах отрезка функция f(x) = x³ – 7 принимает разные знаки. f(1)=-6, а f(3)=20, следовательно корень внутри этого интервала.

2. Находим первую и вторую производную функции f(x):

f^’ (x) = 3x², f^’’ (x) = 6x.

1. За х₀ принимаем тот конец интервала, где знаки функции и второй производной совпадают. Это условие выполняется в точке х₀ =3.
2. Проводим расчеты по формуле метода Ньютона и результаты заносим в таблицу.

а) Задаем нулевое приближение x₀ =3, вычисляем значение функции f(x)=20 и ее производной f^’ (3)=27.

б) Затем находим отношение f(3)/f^’ (3)=0.7407 и вычисляем очередное значение

x₁ = x₀ –f(x₀)/f (x₀):

x₁ = 3 – 20/27 = 3-0.7407 = 2.2593.

в) Аналогично находим х₂ и т. д.

Результаты расчетов заносим в таблицу

n	x	f (x)	f’ (x)	f(x)/f’ (x)
				0.7407
	2.2563	4.5325	15.3133	0.2960
	1.9633	0.5676	11.5636	0.0491
	1.9142	0.0139	10.9925	0.0013
	1.9129	-0.0003

г) На четвертой итерации значение f(x) по модулю меньше заданной точности, поэтому дальнейшие расчеты не проводим.

Ответ: Корень уравнения равен 1.9129.

 

Задача 2. Линейная регрессия.

Уравнение линейной регрессии y(x) = a + bx, где и где черта сверху означает среднее значение.

Пример решения:

По данным таблицы построить аппроксимационный многочлен первой степени, т.е. найти уравнение линейной регрессии. Оценить степень приближения.

i
x
y	-1

Решение: для решения задачи составляются таблицы, содержащая значения необходимые для расчетов. Расчеты удобно проводить используя пакет Excel.

1. Таблица для нахождения коэффициентов а иb.

 

 

В таблице индекс sr обозначает среднее значение соответствующих переменных.

 

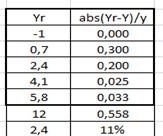1. Для оценки качества модели составляется вторая таблица:

В этой таблице приводятся значения Yr, вычисленные по уравнению регрессии и относительные отклонения расчетных и табличных оценок, взятые по модулю.

В предпоследней строке соответствующие суммы, а в последней их средние значения. 11% - это средняя погрешность модели, которую можно считать удовлетворительной.

1. Приведем график, полученный на компьютере:

На нем отмечены табличные значения, вид уравнения и коэффициент детерминации R².

Он показывает долю вариаций, объясненную регрессией.

 

 

Задача 3. Численное интегрирование.

Интервал интегрирования разбивается на n интервалов. Затем находится шаг h и Xi:

h=(b-a)/n, Xi= a + i*h.Здесь а – нижний предел, в – верхний предел, n – число участков разбиения.

Для численного интегрирования используются квадратурные формулы

, где Xi некоторые точки на отрезке [a,b].

Для используемых формул левых, правых и средних прямоугольников имеем:

.

Решение примера(S = 0):

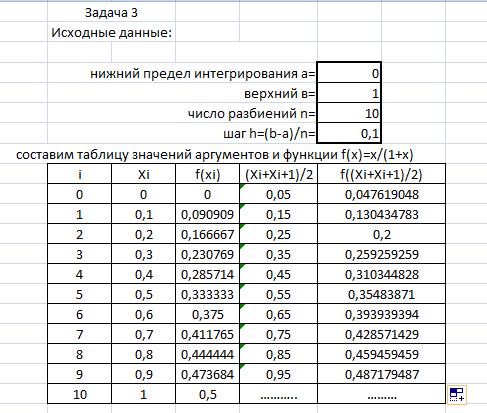
По данным таблицы и приведенным выше формулам находим значения интеграла по различным формулам

Сравним с точными значениями

Делаем вывод, что формула средних прямоугольников обеспечивает удовлетворительную точность.

Литература

Основная

1. Численные методы. / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. 5-е изд. – М.: БИНОМ. 2007. – 636 с.
2. Численные методы (линейная алгебра и нелинейные уравнения) / Вербжицкий.- М.: ООО «издательский дом «ОНИКС»», 2005.-432 с.
3. Численные методы (математический анализ и обыкновенные дифференциальные уравнения) / Вербжицкий.- М.: ООО «издательский дом «ОНИКС»», 2005.-400 с.
4. Численные методы. / Е.А. Волков.-М.: Наука, 1987. – 248 с.

 

Дополнительная

1. Численные методы анализа. / Б.П. Демидович, И.А. Марон, Э.З. Шувалова. – М.: Физматгиз, 1963, 400 с.
2. Основы вычислительной математики / Б.П. Демидович, И.А. Марон. –М.: Физматгиз, 1966, 664 с.
3. Численные методы решения инженерных задач в пакете MathCAD/ И.А. Бедарев, О.Н. Белоусова, Н.Н. Федорова. Новосибирск, СИБСТРИН, 2005, 96 с.
4. Интернет – ресурсы по темам

 

 

Поделиться:

Воспользуйтесь поиском по сайту: