На плоскости даны две окружности (известны координаты центра и радиусы). Требуется проверить, пересекаются ли они.

Обмен значениями

Поменять значения переменных A и B между собой:

а) используя дополнительную переменную;

б) не заводя дополнительных переменных.

Два бандита»

(Время: 1 сек. Память: 16 Мб Сложность: 4%)

Бандиты Гарри и Ларри отдыхали на природе. Решив пострелять, они выставили на бревно несколько банок из-под пива (не больше 10). Гарри начал простреливать банки по порядку, начиная с самой левой, Ларри — с самой правой. В какой-то момент получилось так, что они одновременно прострелили одну и ту же последнюю банку.

Гарри возмутился и сказал, что Ларри должен ему кучу денег за то, что тот лишил его удовольствия прострелить несколько банок. В ответ Ларри сказал, что Гарри должен ему еще больше денег по тем же причинам. Они стали спорить кто кому сколько должен, но никто из них не помнил сколько банок было в начале, а искать простреленные банки по всей округе было неохота. Каждый из них помнили только, сколько банок прострелил он сам.

Определите по этим данным, сколько банок не прострелил Гарри и сколько банок не прострелил Ларри.

Входные данные: 2 числа — количество банок, простреленных Гарри и Ларри соответственно.

Выходные данные: 2 числа — количество банок, не простреленных Гарри и Ларри соответственно.

Журавлики»

(Время: 1 сек. Память: 16 Мб Сложность: 7%)

Петя, Катя и Сережа делают из бумаги журавликов. Вместе они сделали S журавликов. Сколько журавликов сделал каждый ребенок, если известно, что Петя и Сережа сделали одинаковое количество журавликов, а Катя сделала в два раза больше журавликов, чем Петя и Сережа вместе?

Зарплата»

(Время: 1 сек. Память: 16 Мб Сложность: 4%)

В отделе работают 3 сотрудника, которые получают заработную плату в рублях. Требуется определить: насколько зарплата самого высокооплачиваемого из них отличается от самого низкооплачиваемого.

Расстояния в Плоском мире

Плоский мир имеет форму диска. Существует только одна дорога, ведущая с севера на юг диска. Эта дорога проходит через центр диска и её называют Осевой. Остальные дороги проложены с запада на восток или с востока на запад от городов Плоского мира до Осевой дороги. Если два города не расположены на одном отрезке дороги, ведущем до Осевой дороги, то, чтобы добраться из одного города в другой, путешественникам нужно сначала дойти до Осевой дороги, затем дойти до дороги, ведущей в нужный город, и затем по ней дойти до города.

Установим систему координат следующим образом. Центр диска имеет координаты (0,0). Ось Y совпадает с Осевой дорогой. Пусть один город имеет координаты (X ₁,  Y ₁), а другой город – координаты (X ₂,  Y ₂). Тогда расстояние между городами, у которых Y ₁ ≠  Y ₂, вычисляется по формуле| X ₁| + | X ₂| + | Y ₁− Y ₂|, а расстояние между городами, у которых Y ₁ =  Y ₂, вычисляется по формуле | X ₁ −  X ₂|.

Напишите программу, определяющую расстояние, которое нужно пройти по дорогам, чтобы попасть из города с координатами (X ₁,  Y ₁) в город с координатами (X ₂,  Y ₂).

Игра»

(Время: 1 сек. Память: 16 Мб Сложность: 4%)

В свободное время одноклассники Вася и Петя любят играть в различные логические игры: морской бой, крестики-нолики, шахматы, шашки и многое другое. Ребята уже испробовали и поиграли во всевозможные классические игры подобного рода, включая компьютерные. Однажды им захотелось сыграть во что-нибудь новое, но ничего подходящего найти не удалось. Тогда Петя придумал следующую игру «Угадайка»: Играют двое участников. Первый загадывает любое трехзначное число, такое что первая и последняя цифры отличаются друг от друга более чем на единицу. Далее загадавший число игрок переворачивает загаданное число, меняя первую и последнюю цифры местами, таким образом получая еще одно число. Затем из максимального из полученных двух чисел вычитается минимальное. Задача второго игрока – угадать по первой цифре полученного в результате вычитания числа само это число. Например, если Вася загадал число 487, то перестановкой первой и последней цифры он получит число 784. После чего ему придется вычесть из 784 число 487, в результате чего получится число 297, которое и должен отгадать Петя по указанной первой цифре «2», взятой из этого числа. Петя успевает лучше Васи по математике, поэтому практически всегда выигрывает в играх такого типа. Но в данном случае Петя схитрил и специально придумал такую игру, в которой он не проиграет Васе в любом случае. Дело в том, что придуманная Петей игра имеет выигрышную стратегию, которая заключается в следующем: искомое число всегда является трехзначным и вторая его цифра всегда равна девяти, а для получения значения последней достаточно отнять от девяти первую, т.е. в рассмотренном выше случае последняя цифра равна 9-2=7. Помогите Пете еще упростить процесс отгадывания числа по заданной его первой цифре, написав соответствующую программу.

 

1) Дан размер файла в байтах. Переведите эту величину в килобайты.

2) Дана масса M в килограммах. Используя операцию деления нацело, найдите количество полных тонн в ней.

3) С некоторого момента прошло 234 дня. Сколько полных недель прошло за этот период?

4) Даны целые положительные числа A и B (A > B). На отрезке длины A размещено максимально возможное количество отрезков длины B (без наложений). Определите длину незанятой части отрезка A, а также количество отрезков B, размещенных на отрезке A.

5) Дано двузначное число. Найдите сумму и произведение его цифр.

6) Дано трехзначное число. Выведите число, полученное при прочтении исходного числа справа налево.

7) Дано трехзначное число. В нем зачеркнули первую слева цифру и приписали ее справа. Выведите полученное число.

8) Дано трехзначное число. В нем зачеркнули первую справа цифру и приписали ее слева. Вывести полученное число.

9) С начала суток прошло N секунд. Определите: а) сколько полных часов прошло с начала суток; б) сколько полных минут прошло с начала очередного часа; в) сколько полных секунд прошло с начала очередной минуты.

10) Дни недели пронумерованы следующим образом: 0 — воскресенье,1 — понедельник, 2 — вторник, ..., 6 — суббота. Дано целое число K, лежащее в диапазоне 1–365. Определите номер дня недели для K -го дня года, если известно, что в этом году 1 января было понедельником (четвергом, субботой, днем недели с номером N).

11) Даны целые положительные числа A, B, C. На прямоугольнике размера A × B размещено максимально возможное количество квадратов со стороной C (без наложений). Найдите количество квадратов, размещенных на прямоугольнике, а также площадь незанятой части прямоугольника.

12) Дан номер некоторого года (целое положительное число). Определите соответствующий ему номер столетия, учитывая, что, к примеру, началом 20 столетия был 1901 год.

 

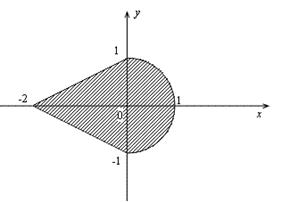
1) Определить, попадет ли точка в заштрихованную область

Ограничения: время – 2s, память – 32MB

2) Определить f(x)

Ограничения: время – 2s, память – 32MB

3) Выяснить, можно ли прямоугольник со сторонами a,  b уместить внутри прямоугольника со сторонами c,  d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.

4) Студент добирался домой в другой город: вначале на автобусе t1 часов со скоростью v ₁, затем на велосипеде t ₂ часов со скоростью v ₂, затем пешком t ₃ часов со скоростью v ₃. В середине пути он делал остановку в придорожном кафе. На чем он тогда передвигался?

Новая столешница

Ограничения: время – 2s, память – 256 MB

Владелец трактира "Залатанный барабан" Чарли решил изменить форму столешницы стойки бара с прямоугольной на треугольную, чтобы ему не приходилось вставать со стула, когда он собирает кружки, оставленные посетителями на углу барной стойки. Но новую столешницу нужно внести в трактир через какое-нибудь окно или дверь.

Напишите программу, которая определяет по размерам столешницы и проема в стене, можно ли внести столешницу в трактир через этот проем. Толщину столешницы считать несущественной. Столешницу можно поворачивать при затаскивании любым образом.

6) Составить программу, которая будет находить, на сколько квадратов, стороны которых выражены натуральными числами, можно разрезать данный прямоугольник, если от него каждый раз отрезается квадрат максимально большой площади.

На плоскости даны две окружности (известны координаты центра и радиусы). Требуется проверить, пересекаются ли они.

Симметрия

Многие из вас, вероятно, знакомы с понятием симметрии относительно прямой. Пусть на плоскости расположена прямая L и точка A. Точка B называется симметричной точке A относительно прямой L, если отрезок АВ перпендикулярен прямой L и делится пополам точкой пересечения с ней. В частности, если точка А лежит на прямой L, то точка B совпадает с точкой А.

Задана прямая L, параллельная одной из осей координат, и точка А. Найдите точку В, симметричную А относительно L.

9. Дано целое число. Если оно является положительным (сюда же относится и нулевое значение), то прибавить к нему 1; в противном случае вычесть из него 2. Вывести полученное число.

10. Ввести два числа. Если хотя бы одно из них является положительным, выдать оба числа на экран. Если же оба числа – отрицательны, выдать на экран сообщение: «Вы не ввели ни одного положительного числа».

11. Создайте приложение, позволяющее правильно (с опорой на область допустимых значений) вычислять арифметическое выражение. Исходные данные вводить с использованием текстового поля (выражения возьмите из пр. работ №3 и 4).

12. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной сумму этих значений, а если равны, то присвоить переменным нулевые значения. Вывести новые значения переменных A и B

13. Создайте проект решения квадратного уравнения.

14. Определите четность или нечетность введенного числа.

15. Имеется дискета объемом N Мбайт. Определите, поместится ли на нее печатный труд на М листах при К строчках на странице и L символов в строке. Определите объем свободного места на дискете.

16. Ввести три числа. Вывести на экран те из них, которые принадлежат интервалу (2,5 – 5,2).

17. В компьютер вводятся длины трех отрезков. Ваш проект должен отвечать на вопрос: можно ли образовать треугольник с такими сторонами?

18. В компьютер вводятся значения трех углов в градусах. Ваш проект должен отвечать на вопрос: можно ли образовать треугольник с такими углами? Дополните задачу указанием типа треугольника: остроугольный, прямоугольный, тупоугольный.

19. Дракон каждый год отращивает по 3 головы, но после того, как ему исполнится 100 лет, - только по две. Ответьте в своем проекте, сколько голов и глаз у дракона, которому N лет?

20. Создайте проект «Угадай число!». При каждом запуске этого проекта случайным образом задумывается число от 1 до 10. Задача пользователя отгадать это число. При этом, в проекте должны даваться пояснения: «Недобор» или «Перебор».

Можно еще подсчитать количество попыток отгадывания, а кроме того еще и дать возможность выбора диапазона чисел (от 1 до 10 или от 1 до 100).

21. Ваня наблюдает за лягушкой. Изначально она сидит в точке 0 числовой прямой. Каждую секунду она прыгает на 1 вправо, пока не достигнет точки K. Затем она начинает каждую секунду прыгать на 1 влево, пока не вернется в точку 0,затем – опять вправо и т.д. Требуется определить, где окажется лягушка через T секунд.(ветвление)

 

1)	Даны натуральные числа х и у, определяющие возраст двух друзей. Из данных чисел напечатать те, которые обозначают "школьный" возраст, то есть от 7 до 16 лет.
2)	Три поросенка: Ниф-Ниф, Нуф-Нуф и Наф-Наф — нашли под дубом желуди. Каждый из них набрал себе приличный запас на зиму (дано три числа). Составить программу, ко­торая бы определяла, кто из поросят поленился и набрал меньше всех.
3)	Федя пытается протолкнуть в форточку размера­ми X см и У см свою голову диаметром не более D см. Удастся ли мальчику его эксперимент, или его голова застрянет?
4)	Войдет ли в конверт размерами х см и у см прямоугольная открытка размерами К см и N см?
5)	Дама сдавала в багаж коробку и пустой чемодан с соответствующими размерами х, у, z и х1,у1, z1. Удастся ли сэкономить место в багажном отделении, поместив данную коробку в чемодан, если стороны коробки и чемодана будут параллельны?
6)	Сестры подсчитали свои денежные накопления: у них оказались разные суммы. Какая сестра должна дать другой денег и сколько, чтобы у обеих сестер суммы стали равными?
7)	В какой из трех весовых категорий будет выступать тяжелоатлет, если его вес G кг, а весовые границы трех категорий соответственно: XN..XK, YN..YK, ZN..ZK?
8)	В туристической фирме клиенту на выбор были предложены три путевки (про каждую известны стоимость N1, N2 и N3 и продолжительность тура Dl, D2 и D3 дней). Какую из трех путевок может выбрать турист, если в его распоряжении X денег и У дней отпуска?
9)	Жители Норвегии, Швеции и Финляндии спорили, где зима холоднее, называя среднюю температуру января в своих столицах. Определите, в каких странах эта температура оказалась ниже средней температуры января в Челябинске (t = — 13°С).
10)	За контрольную работу в классе ученикамибыло получено Р пятерок, СН четверок, TR троек и DV двоек. Определить: а) сколько человек учится в классе; б) каков средний балл; в) сколько учеников получили оценку, превышающую средний балл?
11)	Создайте проект «Угадай число!». При каждом запуске этого проекта случайным образом задумывается число от 1 до 10. Задача пользователя отгадать это число. При этом, в проекте должны даваться пояснения: «Недобор» или «Перебор». Можно еще подсчитать количество попыток отгадывания, а кроме того еще и дать возможность выбора диапазона чисел (от 1 до 10 или от 1 до 100).
12)	Год является високосным, если его номер кратен 4. однако, из кратных 100, високосными являются лишь кратные 400 (например, 1700, 1800 и 1900 – невисокосные, 2000 – високосный). Дано натуральное число N. Определить, является ли високосным год с таким номером.

 

Для решения задачи проще всего использовать формулу Герона:

Зная площадь столешницы S, можно найти её минимальный боковой размер – высоту: h_c =2 S / C. И остается только сравнить высоту столешницы с диагональю прямоугольного проёма, которую можно вычислить по теореме Пифагора: d ²= W ² +  H ². Можно не вычислять корни, а сравнить квадраты высоты h_c и диагонали d (так как функция корня является монотонно возрастающей), и даже обойтись без сравнения дробных чисел, домножив обе части неравенства на знаменатель (так как знаменатель положительный).

 

var a,b,c,w,h:int64;

Begin

read(a,b,c);

read(w,h);

if (a+b+c)*(a+b-c)*(a-b+c)*(-a+b+c)<=4*c*c*(w*w+h*h) then

writeln('YES')

Else

writeln('NO');

end.

 

 

Формат входных данных:
Входной файл input.txt состоит из одной строки, содержащей два натуральных числа - стороны прямоугольника.
Формат выходных данных:
Выходной файл output.txt содержит одно число - количество квадратов

input.txt:
3 4
6 4
output.txt:
3

Решение:
Обозначим стороны прямоугольника за A и B. Сделаем так, чтобы A было больше B (например, с помощью процедуры swap, как в задаче 1001. Теперь заведем переменную C, в которой будет храниться количество квадратиков. Будем повторять следующие действия пока одна из сторон (B) не станет равна 0:
1) B меньше чем A, следовательно, надо откромсать сколько можем квадратов B*B от прямоугольника A*B. Т.е. C:= C + A div B;
2) Вычислим размеры останков прямоугольника: A:= A mod B (не смогли отрезать).
3) swap(A, B)!!!!!

 

Поделиться:

Воспользуйтесь поиском по сайту: