При этом в левой части с плюсом берутся Э.Д.С., направление которых совпадает с направлением обхода контура.

Введение

Методические указания предназначены для студентов закончивших неэлектрических специальностей при изучении электротехники по курсу “ЭОЭ и МПТ”, 4.1.

Указания содержат краткие теоретические сведения и варианты контрольных задач. Данные указания имеют цель повысить эффективность усвоения учебного материала студентами-заочниками и сократить время выполнения расчёта.

Сведение на контрольную работу №1.

Задача№1. Провести анализ линейной цепи постоянного тока.

Задача№2. Анализ линейной цепи переменного синусоидального тока.

Задача№3. Анализ трёхфазной электрической цепи при схеме соединения приёмников “звездой”.

Задача№4. Анализ трёхфазной электрической цепи при схеме соединения приёмников “треугольником”.

Задача№5. Провести анализ работы однофазного трансформатора.

Задача№6. Провести расчёт режима работы асинхронного двигателя.

 

Требования к контрольной работе.

1. Контрольная работа выполняется в тетради в клетку аккуратным разборчивым почерком.

2. Все схемы расчётные, таблицы и векторные диаграммы выполнять карандашом.

3. Задачи должны содержать исходные данные по вашему варианту, сведённые в таблицу, электрическую схему и необходимые пояснения к ходу решения. Все вычисления приводить в решении задач.

4. Контрольная работа отправляется на рецензию заранее. При наличии замечаний в той же тетради приводится исправленный вариант.

 

 

Задача№1 Анализ линейной цепи постоянного тока.

I. Схемы электрических цепей показаны на рис.1.

Параметры элементов схемы помещены в таблице1.

Требуется:

1. Составить уравнения по законам Кирхгофа (не решая их).

2. Определить токи ветвей методом контурных токов.

3. Составить баланс мощностей, провести проверку решения.

4. Определить показания вольтметра.

 

II. Краткие теоретические положения.

2.1 Законы Кирхгофа

Первый закон Кирхгофа. Алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю. Σi=0.

Второй закон Кирхгофа. В замкнутом электрическом контуре алгебраическая сумма всех источников Э.Д.С. равна алгебраической сумме падений напряжений на сопротивлениях контура Σе=Σir.

При этом в левой части с плюсом берутся Э.Д.С., направление которых совпадает с направлением обхода контура.

Уравнения по законам Кирхгофа записывают для независимых узлов и контуров.

Независимый узел – это узел, в который входит хотя бы одна новая ветвь по сравнению с остальными узлами.

Независимый контур-это контур, включающий по крайней мере одну новую ветвь и ветви выбранных ранее контуров.

 

2.2 Баланс мощностей.

Сумма мгновенных значений мощностей источников в электрической цепи равна сумме мгновенных значений мощностей, потребляемых этой цепью ΣРгенер=ΣРпотр.; Σ±Е_j I_j=ΣI_j²R_j.

При этом в левой части произведение с плюсом, если направления Э.Д.С. и тока совпадают.

 

2.3. Метод контурных токов.

Метод контурных токов позволяет уменьшить количество уравнений, составляемых по законам Кирхгофа, до числа уравнений, оставленных по второму закону Кирхгофа. Контурными называются условные (расчётные) токи, замыкающиеся только по своим контурам. Направлениями контурных токов задаются произвольно.

Ток любой ветви находят как алгебраическую сумму контурных токов, замыкающихся по этой ветви.

 

2.4. Метод межузловых потенциалов.

В общем случае составляют столько же уравнений, сколько и по первому закону Кирхгофа. Один из узлов схемы можно заземлить.

Запишем уравнения в матричной форме для остальных узлов схемы:

 

 

g_a g_ab g_ac φ_a I_a

g_ba g_b g_bc * φ_b = I_b

g_сa g_сb g_с φ_c I_c

 

В матрицу проводимостей входят собственные и взаимные проводимости ветвей. Собственные проводимости ветвей (g_a,g_b,g_c) равны алгебраической сумме проводимостей ветвей, входящих в узел. Взаимные проводимости - это проводимости ветвей, соединяющих интересующие узлы. Причём взаимные проводимости всегда отрицательны.

Узловые токи равны алгебраической сумме произведений Э.Д.С. на проводимость ветвей, входящих в узел.

Ia= Σ±Eg, причём плюс, если Э.Д.С. направлена к узлу.

Токи в ветвях находят, применяя обобщённый закон Ома.

 

2.5 Метод эквивалентного генератора.

Метод эквивалентного генератора применяется для частичного анализа электрических цепей, необходимо исследовать режим работы одной из ветвей цепи, при этом полный расчёт электрической цепи не производится (рис.2.). Электрическую цепь относительно выделенной ветви можно представить в виде активного двухполюсника, и тогда ток в ветви можно определить как

 

I_ab=U_xx/(R_ab+R_b),

где Uxx – напряжение на зажимах АВ при R_b= ∞;

R_b – сопротивление выделенной цепи;

R_ab – сопротивление электрической цепи относительно зажимов АВ при отключённом сопротивлении Rв. При этом все источники Э.Д.С. закорачиваются, источники тока разрываются.

Таблица№1.

№ вар

Е1

Е2

Е3

Е4

Е5

Е6

R1

R2

R3

R4

R5

R6

R7

R8

R9

R10

В

Ом

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

 

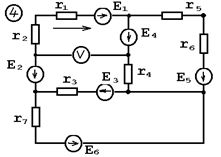
Рис.1

 

Задача №2. Анализ линейной цепи переменного синусоидального тока.

Схема электрической цепи показана на рис.3. Параметры элементов схемы помещены в таблице 2.

Электрическая цепь переменного синусоидального тока с частотой f=50Гц. Находится под действием источника напряжения е =Еmsin(ωt+φe). С учётом положения выключателей В1- В7 определить для своего варианта:

1) полные и комплексные сопротивления участков цепи;

2) полные и комплексные проводимости участков цепи;

3) все токи ветвей;

4) полные, реактивные и активные мощности отдельных участков цепи и всей электрической цепи;

5) построить векторные диаграммы токов и напряжений;

 

IV. Краткие теоретические положения.

4.1 Формы представления синусоидальных величин.

а) тригонометрическая форма записи мгновенных величин

i=Imsin(ωt+φi);

 

Таблица 2.

№

Em,B

φe,˚

Ul3,B

I3,A

R1,Ом

R2,Ом

R3,Ом

R4,Ом

R5,Ом

Xl2,Ом

Xl3,Ом

Xl6,Ом

Xc1, Ом

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

Таблица 2 (продолжение)

			-	-	-		-					-	-
			-	-		-		-	-	-
	-	-				-				-
			-	-	-		-				-	-	-
	-	-		-		-		-		-
			-	-	-		-				-	-	-
	-	-	-			-				-		-
			-	-		-	-	-		-	-
			-	-	-		-		-		-		-
	-	-		-		-		-		-		-
		- 20		-	-		-	-			-		-
	-	-		-		-	-	-		-	-
	-	-	-		-		-				-		-
			-	-		-		-		-	-
	-	-		-	-		-		-		-		-
	-	-	-			-		-		-		-
	-	-		-	-			-				-	-
		-30	-	-		-		-		-
	-	-		-	-		-	-			-		-
	-	-	-			-		-	-	-
			-	-	-		-				-		-
	-	-		-		-	-	-		-	-
	-	-	-			-		-	-	-
			-	-	-		-		-		-		-
	-	-		-		-		-		-
	-	-	-			-		-	-	-
			-	-	-		-	-			-		-
	-	-		-		-				-		-
	-	-	-			-		-	-	-
			-	-		-	-		-		-		-
	-	-		-		-		-		-		-
	-	-	-			-		-		-
			-	-	-		-				-		-
	-	-		-		-		-		-
	-	-				-		-	-	-

 

 

Таблица 2 (продолжение)

 

№ вар.	Xc4,Ом	Xc7,Ом	Выключате- ли замкнуты	кп.6
			B1,B4,B5,B7	Xc4
	-	-	B2,B3,B5,B6	Xl2
		-	B1,B3,B4,B5	Xc1
			B2,B4,B5,B7	Xc7
	-	-	B2,B3,B5,B6	Xl2
		-	B2,B3,B4,B5	Xl3
	-		B2,B3,B5,B7	Xl3
	-	-	B2,B3,B5,B6	Xl2
		-	B2,B3,B4,B5	Xc4
	-	-	B1,B3,B5,B6	Xl6
		-	B1,B3,B4,B5	Xc4
		-	B2,B3,B4,B5	Xl2
	-	-	B1,B3,B5,B6	Xl3
		-	B1,B3,B4,B5	Xc1
	-	-	B1,B3,B5,B6	Xc1
		-	B2,B4,B5,B6	Xc4
	-		B1,B3,B6,76	Xl3
	-	-	B1,B3,B5,B6	Xc1
			B2,B4,B5,B7	Xc7
	-	-	B1,B3,B5,B6	Xl6
			B2,B4,B5,B7	Xl2
		-	B1,B3,B4,B5	Xl3
	-		B1,B5,B6,B7	Xl6
			B2,B4,B6,B7	Xc4
	-		B1,B3,B5,B7	Xl3
	-		B2,B5,B6,B7	Xc7
	-		B1,B5,B6,B7	Xl6
	-		B2,B3,B5,B7	Xl2
	-	-	B1,B3,B5,B6	Xc1
			B2,B4,B6,B7	Xc7
	-		B1,B3,B5,B7	Xc1
	-		B2,B3,B5,B7	Xl2
	-	-	B1,B3,B5,B6	Xl3
	-		B2,B5,B6,B7	Xc7
	-		B1,B3,B6,B7	Xc1
		-	B2,B4,B5,B6	Xc4
		-	B2,B4,B5,B6	Xl2
	-		B1,B3,B6,B7	Xc1
			B2,B4,B6,B7	Xc7
	-	-	B1,B3,B5,B6	Xl3
	-		B1,B3,B6,B7	Xl3
	-		B2,B5,B6,B7	Xl6
	-	-	B1,B3,B5,B7	Xl3
	-		B1,B3,B6,B7	Xc7
			B2,B4,B6,B7	Xl6
	-		B1,B3,B5,B7	Xc7
	-	-	B1,B3,B5,B6	Xl3
		-	B2,B4,B5,B6	Xl6
	-	-	B1,B3,B5,B6	Xc1
	-		B1,B3,B6,B7	Xc7

 

 

б) форма записи комплексных чисел показательная

 

и алгебраическая

, где

 

Рассмотрим несколько примеров перевода комплексных чисел из алгебраической формы в показательную:

, где , ψ=arctg b/a;

,

,

,

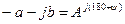где а и b- проекции на ось действительных и мнимых чисел соответственно.

 

4.2 Резонанс напряжений

Резонанс напряжений возможен лишь в электрической цепи, содержащий последовательно включённые реактивные сопротивления X_L и X_C.

Условием возникновения резонанса напряжений является равенство X_L =X_C или ωL=1/(ωc).

 

4.3 Резонанс токов.

Резонанс токов возможен в электрической цепи при параллельном включении реактивных сопротивлений X_L и X_C.

Условием появления резонанса тока является равенство реактивных проводимостей соответствующих ветвей:

b_L= b_С;

где b_L = ; b_С = .

Электрическая схема с параллельным включением реактивных сопротивлений X_L и X_C изображена на рис. 4.

 

 

 

Задача3. Анализ трёхфазной электрической цепи при схеме соединения приёмников “ звездой ”.

 

1) В трёхфазную сеть с симметричной системой линейных напряжений U_Л включён трёхфазный потребитель электроэнергии, фазы которого имеют комплексные сопротивления Z_a, Z_b, Z_c и соединены “звездой”.

Определить:

1) линейные и фазные ток;

2) активную Р, реактивную Q и полную S мощности потребителя;

3) показания приборов: амперметра и ваттметра;

4) построить векторную диаграмму токов и напряжений;

 

5) Краткие теоретические положения.

 

4.1 Трёхфазная система питания потребителей электроэнергии.

Трёхфазная система питания электрических цепей представляет собой совокупность трёх синусоидальных ЭДС или напряжений, одинаковых по частоте и амплитудному значению, сдвинутых по фазе относительно друг друга на угол 120.

е_А = Em sin wt; e_В = Em sin (wt-2П/3)

e_C = Em sin (wt+2П/3).

В симметричных источниках питания максимальные значения ЭДС равны, соответственно равны и действующие значения ЭДС

E_A=E_B=E_C=E_ф. Пренебрегая внутренним сопротивлением источника, можно принять соответствующие ЭДС источника равными напряжениям, действующим на его зажимах:

E_А=U_А, E_В=U_В, E_С=U_С.

Комплексные напряжения симметричного источника питания могут быть представлены системой уравнений:

U _А = U_ф e^j0 = U_ф,

 

U _В = U_ф e^-j120 = U_ф(-0,5- j √3/2),

 

U _С = U_ф e^j120 = U_ф(-0,5+ j √3/2)

 

Фазным называется напряжение между началом и концом фазы. Линейным назовём напряжение между двумя линиями или между началами двух фаз. Соотношение между линейным и фазным напряжениями симметричного источника питания: U_л = √3 U_ф.

 

 

4.2 Трёхфазные электрические цепи при соединении фаз приёмников “звездой”.

При соединении фаз трёхфазного источника питания “звездой” концы фаз источника X,Y,Z объединены в общую нейтральную точку N, а начала фаз А,В,С подключаются к соответствующим линейным проводам Аа, Вв, Сс. Аналогичным образом при соединении трёхфазных потребителей “звездой” объединяются в нейтральную точку n концы его фаз x,y,z, а начала фаз а,в,с подключаются к линейным проводам.

Линейные токи I_л в питающих линиях имеют условно-положительное направление от источника энергии к приёмнику. При соединении приёмника энергии по схеме “звезда” линейные токи I_А,I_В,I_С одновременно являются и фазными токами приёмника Iа,Iв,Iс, т.е.

I_А= I_а; I_В = I_в ; I_С = I_с.

Трёхфазные источники питания практически всегда выполняются симметричными. Трёхфазные потребители электроэнергии могут быть симметричными и несимметричными. Для симметричных приёмников электроэнергии справедливы соотношения, полученные для трёхфазных симметричных источников питания.

При этом U_а= U_b=U_c=U_ф;

U_АВ = U_ВС =U_СА = U_Л; Z_a=Z_b=Z_c=Z_ф;

Cosφ_а = cosφ_b = cosφ_c = Cosφ_ф; U_Л=√3U_ф.

Для несимметричных приёмников не все эти соотношения соблюдаются.

При анализе трёхфазных электрических цепей широко используется метод комплексных чисел.

При несимметричной нагрузке комплексные сопротивления фаз приёмника не одинаковы (Z_a≠Z_b≠Z_c), при этом комплексное напряжение U_nN, действующее между нейтральными точками N и n системы, определяют по методу двух узлов

ַ U_nN=

где U_A, U_B,U_C – комплексные напряжения источника питания.

Yַ_a = 1/Z_a ; Y_b = 1/Z_b; Y_c= 1/Z_c; Y_N = 1/Z_N – комплексные проводимости фаз и нейтрального провода.

Комплексный ток в нейтральном проводе находят в соответствии с уравнением, составленным по первому закону Кирхгофа для нейтральнoй точки n цепи:

 

I_n۠=I_a+I_b+I_c.

Комплексные фазные напряжения приёмника электроэнергии находят из уравнений; составленных по второму закону Кирхгофа для замкнутого контура:

 

U_a=U_A- U_nN; U_b=U_B- U_nN; U_c=U_C- U_nN.

 

При этом фазные токи приёмника определяют по закону Ома для соответствующих участков цепи:

 

I_a=U_a/Z_a; I_b=U_b/Z_b; I_c=U_c/Z_c.

 

Трёхфазная система обеспечивает приёмники электроэнергии симметричным питанием. При этом активная, реактивная и полная мощности могут быть определены по следующим формулам с учётом знака реактивных сопротивлений:

P = I_А²R_а + I_В²R_b + I_С²R_c =U_aI_A cosφ_а + U_b I_B cosφ_b +U_cI_C cosφ_с;

Q= I_А²X_a + I_В²X_b + I_С²X_c =U_a I_A sinφ_а + U_b I_b sinφ_b + U_c I_С sinφ_с;

S = √P²+Q² = I_А²Z_a + I_В²Z_b + I_С²Z_c;

 

где cosφ_а= R_a/ Z_a; cos φ_b = R_b/ Z_b; cos φ_с= R_c/ Z_c

sin φ_а= X_a/ Z_a; sin φ_b = X_b/ Z_b; sin φ_с = X_c/ Z_c.

При симметричной нагрузке эти формулы приводят к виду:

P= 3 I_ф²R_ф= √3U_Л I_Л cos φ_ф;

Q= 3 I_a²Xa= √3U_K I_K sin φ_a$

S= √P²+Q² = √3U_Л I_Л,

где cos φ_ф = R_ф/ Z_ф; sin φ_ф = X_ф/ Z_ф.

 

6.3 Несимметричные режимы в трёхфазной электрической цепи при соединении приёмников электроэнергии “звездой”

При обрыве линии (или фазы приёмника электроэнергии) в трёхпроводной системе Y-проводимость соответствующей фазы приёмника, например фазы С равна нулю, т.к. сопротивление равно ∞. Следовательно, несколько изменится напряжение между нейтральными точками системы UnN:

U_nN= , где Yc=0

Фазные напряжения приёмника определяют как:

U_a=U_А- U_nN; U_b=U_В- U_nN; U_c=U_С- U_nN.

Фазные токи приёмника по закону Ома:

I_a=U_a/Z

Поделиться:

Воспользуйтесь поиском по сайту: