 |
Распределённых случайных величин
|
|
|
|
Общие методические указания
При выполнении практических работ студенту необходимо руководствоваться следующим:
1) работа должна быть выполнена в среде Microsoft Office Excel;
2) Формулировка задания и пример выполнения приведены ниже.
Содержание второй части семестровой (контрольной) работы соответствует примерам практических работ (примеры 3.1; 3.2; 3.3; 3.4; 3.5; 3.6; 3.7; 3.8; 3.9). Каждое задание имеет индивидуальные исходные данные (приложение А).
Студент должен быть готов во время отчёта семестровой (контрольной) работы дать пояснения по существу выполнения работы.
Проверка статистических гипотез
Критерии для отбрасывания резко выделяющихся
Результатов испытаний
Иногда причины резких отклонений опытных данных не обнаруживаются во время проведения экспериментов, однако отдельные значения всё же вызывают сомнение. В подобных случаях их исключают путём применения специальных критериев.
Нулевой гипотезой при использовании критериев является предположение о том, что наибольшее значение х n (или наименьшее х 1) принадлежит той же генеральной совокупности, что и все остальные n – 1 наблюдений.
Критерий для отбрасывания при известной генеральной дисперсии. Использование рассматриваемого критерия возможно для нормально распределённой случайной величины при неизвестном математическом ожидании и известном значении генеральной дисперсии. Подобная ситуация встречается например для тех характеристик механических свойств материала, которые контролируются при сдаче и приёмке продукции.
Результаты испытаний анализируемой выборки представляют в виде вариационного ряда. По формуле (4) или (14) производят оценку математического ожидания.
|
|
|
Далее вычисляют статистику
t 1 = 
или t n = 
(3.1)
и сравнивают с критическим значением t α взятым из таблицы 3.1.
Если выполняется неравенство
t 1 ≤ t α или t n ≤ t α (3.2)
то нулевая гипотеза не отклоняется, т.е. результат испытания х 1 или х n не следует считать выбросом.
Таблица 3.1 – Критические значения t α и u α
| n | t α | u α | ||||
| α = 0,10 | α = 0,05 | α = 0,01 | α = 0,10 | α = 0,05 | α = 0,01 | |
| 1,50 1,70 1,84 1,94 2,02 2,09 2,15 2,20 2,24 2,28 2,32 2,35 2,38 2,41 2,43 2,46 2,48 2,50 2,52 2,54 2,56 2,57 2,59 2,70 2,79 2,86 3,08 3,34 3,53 | 1,74 1,94 2,08 2,18 2,27 2,33 2,39 2,44 2,48 2,52 2,56 2,59 2,62 2,64 2,67 2,69 2,71 2,73 2,75 2,77 2,78 2,80 2,82 2,93 3,02 3,08 3,29 3,53 3,70 | 2,22 2,43 2,57 2,68 2,76 2,83 2,88 2,93 2,97 3,01 3,04 3,07 3,10 3,12 3,15 3,17 3,19 3,21 3,22 3,24 3,26 3,27 3,28 3,40 3,48 3,54 3,72 3,95 4,11 | 1,15 1,42 1,60 1,73 1,83 1,91 1,98 2,03 2,09 2,13 2,17 2,21 2,25 2,28 2,31 2,34 2,36 2,38 2,41 2,43 2,45 2,47 2,49 | 1,15 1,46 1,67 1,82 1,94 2,03 2,11 2,18 2,23 2,29 2,33 2,37 2,41 2,44 2,48 2,50 2,53 2,56 2,58 2,60 2,62 2,64 2,66 | 1,15 1,49 1,75 1,94 2,10 2,22 2,32 2,41 2,48 2,55 2,61 2,66 2,70 2,75 2,78 2,82 2,85 2,88 2,91 2,94 2,96 2,99 3,01 |
В противном случае гипотеза отклоняется, т.е. результат х 1 или х n является ошибочным и должен быть исключён из дальнейшего анализа, а найденная ранее оценка математического ожидания должна быть скорректирована.
Критерий Н. В. Смирнова. Использование критерия Н. В. Смирнова также предполагает нормальное распределение изучаемой случайной величины. Критерий действителен для случаев при которых генеральные параметры неизвестны, а известны лишь их оценки, произведённые на основании анализируемой выборки.
Вычисляют статистику
u 1 = 
или u n =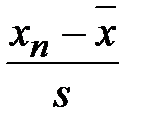 
(3.1,а)
и сравнивают с критическим значением u α взятым из таблицы 3.1. При n > 25 рекомендуется принимать u α = t α.
Если выполняется неравенство
u 1 ≤ u α или u n ≤ u α (3.2, а)
то нулевая гипотеза не отклоняется, т.е. результат испытания х 1 или х n не следует считать выбросом. В противном случае гипотеза отклоняется.
|
|
|
Пример 3.1. По результатам примера 2.1 проверить нулевую гипотезу о принадлежности последнего образца вариационного ряда той же генеральной совокупности, как и остальные образцы.
= 453
s = 11,26
u n = 
= 
= 2,13.
u n = 2,13 < u α
Заключение: нулевая гипотеза не отклоняется, т.е. результат x 20 = 177 не является следствием грубой ошибки эксперимента.
Критерии равенства дисперсий двух нормально
распределённых случайных величин
Сравнение выборочной дисперсии с известной генеральной. В некоторых случаях имеющийся большой экспериментальный материал позволяет с высокой точностью и статистической надёжностью оценить генеральную дисперсию исследуемой величины σ20.
Допустим, что в связи с изменением технологии производства деталей была испытана серия образцов объёмом n, по результатам которой вычислена оценка дисперсии s 2. Требуется проверить нулевую гипотезу Н 0, заключающуюся в том, что дисперсия σ2 генеральной совокупности, из которой взята выборка, равна σ20. Рассмотрим решение этой задачи при трёх возможных альтернативных гипотезах Н А.
1) Н А: σ2 > σ20. Если для выбранного уровня значимости α выполняется неравенство
≤ 
, (3.3)
то нулевую гипотезу σ2 = σ20 не отклоняют.
Если неравенство (3.3) несправедливо, то принимают альтернативную гипотезу σ2 > σ20.
2) Н А: σ2 < σ20. Если для выбранного уровня значимости α выполняется неравенство
≥ 
, (3.4)
то нулевую гипотезу σ2 = σ20 не отклоняют.
Если неравенство (3.4) несправедливо, то принимают альтернативную гипотезу σ2 < σ20.
3) Н А: σ2 ≠ σ20. Если для выбранного уровня значимости α выполняются неравенства
≤ ≤ 
, (3.5)
то нулевую гипотезу σ2 = σ20 не отклоняют.
Если неравенства (3.5) несправедливо, то принимают альтернативную гипотезу σ2 ≠ σ20.
При использовании критериев значимости, важно, задаваясь приемлемой величиной уровня значимости α, обеспечить достаточно низкую вероятность ошибки второго рода, т.е. иметь достаточно высокую уверенность в браковке нулевой гипотезы в то время, когда верна альтернативная. Для повышения уверенности при значениях n ≥ 15 минимально необходимый объём выборки можно найти по формуле:
|
|
|
n = 1,5 + 0,5 
, (3.6)
где Δσ – максимальное относительное расхождение (ошибка) в средних квадратических отклонениях при принятии нулевой гипотезы, λ2 = 
= (1 +Δσ)2 – мощность одностороннего критерия.
В случае использования двустороннего критерия (3.5)
n = 1,5 + 0,5 
, (3.7)
Таблица 3.2 – Минимально необходимый объём выборки n при проверке гипотезы σ2 = σ20
| β | α | Δσ | ||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | ||
| 0,05 | 0,05 0,06 0,07 0,08 0,09 0,10 | |||||
| 0,01 | 0,05 0,06 0,07 0,08 0,09 0,10 |
Пример 3.2. По результатам испытания 20 образцов произведена оценка дисперсии s 2 = 126,9. Проверить нулевую гипотезу, заключающуюся в том, что выборка взята из генеральной совокупности с дисперсией σ20 = 100 против альтернативной σ2 > σ20.
Вычисляем левую часть неравенства (3.3):
= 
=1,269
Задаёмсяα = 0,05 и по таблице 2.10 находим для k = n – 1 = 19
χ20,05 = 30,1
Вычисляем правую часть соотношения (3.3)
= 
= 1,584
Заключение: неравенство (3.3) выполняется, следовательно, нулевую гипотезу не бракуем.
Пример 3.3. Определить минимальный объём выборки для проверки нулевой гипотезы о равенстве дисперсий с помощью двустороннего критерия (3.5), если α = 0,05; β = 0,10 и Δσ = 0,3
По таблице 2.8 находим z 1–β = z 0,9 = 1,282; z 1–α/2 = z 0,975 = 1,960.
На основании формулы (3.7) определяем
n = 1,5 + 0,5 
≈ 75.
Критерий равенства дисперсий двух генеральных совокупностей. Пусть по результатам испытаний двух независимых выборок объёмом n 1 и n 2 из нормально распределённых совокупностей подсчитаны оценки дисперсий, причём s 21 > s 22. Требуется проверить нулевую гипотезу о том, что указанные выборки принадлежат генеральным совокупностям с равными дисперсиями, т.е. σ21 = σ22 = σ2 при альтернативной гипотезе σ21 ≠ σ22. С этой целью используют двусторонний F -критерий (критерий Фишера), для чего находят статистику
F =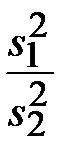 
при s 21 > s 22. (3.8)
И сопоставляют с критическим значением F 1–α/2, представленным в 3.3
Если
F = 
≤ F 1–α/2, (3.9)
то гипотезу о равенстве дисперсий двух генеральных совокупностей, из которых взяты выборки, т.е. σ21 = σ22 = σ2, не отклоняют.
|
|
|
В случае невыполнения неравенства (3.9) нулевую гипотезу отвергают.
При альтернативной гипотезе σ21 > σ22 используют односторонний критерий
F = ≤ F 1–α, (3.10)
если неравенство выполняется, то нулевую гипотезу не отвергают. В противном случае принимают σ21 > σ22.
В случае подтверждения нулевой гипотезы σ21 = σ22 = σ2 по двум выборочным дисперсиям производят новую оценку генеральной дисперсии σ2:
s 2 = 
.
Пример 3.4. В результате испытаний двух партий 30 образцов и 20 образцов соответственно найдены выборочные средние значения и дисперсии предела прочности сплава. α = 0,1.
= 401; s 12 = 82.
= 409; s 22 = 71
Требуется проверить гипотезу о равенстве генеральных дисперсий предела прочности материала при альтернативной гипотезе σ21 ≠ σ22.
В соответствии с соотношением (3.10)
F = 
= 1,15.
Для принятого уровня значимости α = 0,1; k 1 = n 1 – 1 = 29 и k 2 = n 2 – 1 = 19 по таблице 3.3 находим
F 1–α/2 = F 0,95 = 2,08
и сопоставляем с вычисленным значением
F = 1,15 < F 0,95 = 2,08.
Заключение: дисперсии однородны.
Таблица 3.3 – Значение пяти- (верхние строки) и однопроцентных (нижние строки) верхних пределов величин F в зависимости от степени свободы k 1 = n 1 – 1 и k 2 = n 2 – 1
| k 2 | k 1 | ||||||||||||||||
| 18,51 98,49 | 19,00 99,01 | 19,16 99,17 | 19,25 99,25 | 19,30 99,30 | 19,33 99,33 | 19,36 99,34 | 19,37 99,36 | 19,38 99,38 | 19,39 99,40 | 19,40 99,41 | 19,41 99,42 | 19,42 99,43 | 19,43 99,44 | 19,44 99,45 | 19,45 99,46 | 19,46 99,47 | |
| 10,13 34,12 | 9,55 30,81 | 9,28 29,46 | 9,12 28,71 | 9,01 28,24 | 8,94 27,91 | 8,88 27,67 | 8,84 27,49 | 8,81 27,34 | 8,78 27,23 | 8,76 27,13 | 8,74 27,05 | 8,71 26,92 | 8,69 26,83 | 8,66 26,69 | 8,64 26,60 | 8,62 26,50 | |
| 7,71 21,20 | 6,94 18,00 | 6,59 16,69 | 6,39 15,98 | 6,26 15,52 | 6,16 15,21 | 6,09 14,98 | 6,04 14,80 | 6,00 14,66 | 5,96 14,54 | 5,93 14,45 | 5,91 14,37 | 5,87 14,24 | 5,84 14,15 | 5,80 14,02 | 5,77 13,93 | 5,74 13,83 | |
| 6,61 16,26 | 5,79 13,27 | 5,41 12,06 | 5,19 11,39 | 5,05 10,97 | 4,95 10,67 | 4,88 10,45 | 4,82 10,27 | 4,78 10,15 | 4,74 10,05 | 4,70 9,96 | 4,68 9,89 | 4,64 9,77 | 4,60 9,68 | 4,56 9,55 | 4,53 9,47 | 4,50 9,38 | |
| 5,99 13,74 | 5,14 10,92 | 4,76 9,78 | 4,53 9,15 | 4,39 8,75 | 4,28 8,47 | 4,21 8,26 | 4,15 8,10 | 4,10 7,98 | 4,06 7,87 | 4,03 7,79 | 4,00 7,72 | 3,96 7,60 | 3,92 7,52 | 3,87 7,39 | 3,84 7,31 | 3,81 7,23 | |
| 5,59 12,25 | 4,74 9,55 | 4,35 8,45 | 4,12 7,85 | 3,97 7,46 | 3,87 7,19 | 3,79 7,00 | 3,73 6,84 | 3,68 6,71 | 3,63 6,62 | 3,60 6,54 | 3,57 6,47 | 3,52 6,35 | 3,49 6,27 | 3,44 6,15 | 3,41 6,07 | 3,38 5,98 | |
| 5,32 11,25 | 4,46 8,65 | 4,07 7,59 | 3,84 7,01 | 3,69 6,63 | 3,58 6,37 | 3,50 6,19 | 3,44 6,03 | 3,39 5,91 | 3,34 5,82 | 3,31 5,74 | 3,28 5,67 | 3,23 5,56 | 3,20 5,48 | 3,15 5,36 | 3,12 5,28 | 3,08 5,20 | |
| 5,12 10,56 | 4,26 8,02 | 3,86 6,99 | 3,63 6,42 | 3,48 6,06 | 3,37 5,80 | 3,29 5,62 | 3,23 5,47 | 3,18 5,35 | 3,13 5,26 | 3,10 5,18 | 3,07 5,11 | 3,02 5,00 | 2,98 4,92 | 2,93 4,80 | 2,90 4,73 | 2,86 4,64 | |
| 4,96 10,04 | 4,10 7,56 | 3,71 6,55 | 3,48 5,99 | 3,33 5,64 | 3,22 5,39 | 3,14 5,21 | 3,07 5,06 | 3,02 4,95 | 2,97 4,85 | 2,94 4,78 | 2,91 4,71 | 2,86 4,60 | 2,82 4,52 | 2,77 4,41 | 2,74 4,33 | 2,70 4,25 | |
| 4,75 9,33 | 3,88 6,93 | 3,49 5,95 | 2,36 5,41 | 3,11 5,06 | 3,00 4,82 | 2,92 4,65 | 2,85 4,50 | 2,80 4,39 | 2,76 4,30 | 2,72 4,22 | 2,69 4,16 | 2,64 4,05 | 2,60 3,98 | 2,54 3,86 | 2,50 3,78 | 2,46 3,70 | |
| 4,60 8,86 | 3,74 6,51 | 3,34 5,56 | 3,11 5,03 | 2,96 4,69 | 2,85 4,46 | 2,77 4,28 | 2,70 4,14 | 2,65 4,03 | 2,60 3,94 | 2,56 3,86 | 2,53 3,80 | 2,48 3,70 | 2,44 3,62 | 2,39 3,51 | 2,35 3,43 | 2,31 3,34 | |
| 4,49 8,53 | 3,63 6,23 | 3,24 5,29 | 3,01 4,77 | 2,85 4,44 | 2,74 4,20 | 2,66 4,03 | 2,59 3,89 | 2,54 3,78 | 2,49 3,69 | 2,45 3,61 | 2,42 3,55 | 2,37 3,45 | 2,33 3,37 | 2,28 3,25 | 2,24 3,18 | 2,20 3,10 | |
| 4,41 8,28 | 3,55 6,01 | 3,16 5,09 | 2,93 4,58 | 2,77 4,25 | 2,66 4,01 | 2,58 3,85 | 2,51 3,71 | 2,46 3,60 | 2,41 3,51 | 2,37 3,44 | 2,34 3,37 | 2,29 3,27 | 2,25 3,19 | 2,19 3,07 | 2,15 3,00 | 2,11 2,91 | |
| 4,35 8,10 | 3,49 5,85 | 3,10 4,94 | 2,87 4,43 | 2,71 4,10 | 2,60 3,87 | 2,52 3,71 | 2,45 3,56 | 2,40 3,45 | 2,35 3,37 | 2,31 3,30 | 2,28 3,23 | 2,23 3,13 | 2,18 3,05 | 2,12 2,94 | 2,08 2,86 | 2,04 2,77 | |
| 4,30 7,94 | 3,44 5,72 | 3,05 4,82 | 2,82 4,31 | 2,66 3,99 | 2,55 3,76 | 2,47 3,59 | 2,40 3,45 | 2,35 3,35 | 2,30 3,26 | 2,26 3,18 | 2,23 3,12 | 2,18 3,02 | 2,13 2,94 | 2,07 2,83 | 2,03 2,75 | 1,98 2,67 | |
| 4,26 7,82 | 3,40 5,61 | 3,01 4,72 | 2,78 4,22 | 2,62 3,90 | 2,51 3,67 | 2,43 3,50 | 2,36 3,36 | 2,30 3,25 | 2,26 3,17 | 2,22 3,09 | 2,18 3,03 | 2,13 2,93 | 2,09 2,85 | 2,02 2,74 | 1,98 2,66 | 1,94 2,58 | |
| 4,22 7,72 | 3,37 5,53 | 2,98 4,64 | 2,74 4,14 | 2,59 3,82 | 2,47 3,59 | 2,39 3,42 | 2,32 3,29 | 2,27 3,17 | 2,22 3,09 | 2,18 3,02 | 2,15 2,96 | 2,10 2,86 | 2,05 2,77 | 1,99 2,66 | 1,95 2,58 | 1,90 2,50 | |
| 4,20 7,64 | 3,34 5,45 | 2,95 4,57 | 2,71 4,07 | 2,56 3,76 | 2,44 3,53 | 2,36 3,36 | 2,29 3,23 | 2,24 3,11 | 2,19 3,03 | 2,15 2,95 | 2,12 2,90 | 2,06 2,80 | 2,02 2,71 | 1,96 2,60 | 1,91 2,52 | 1,87 2,44 | |
| 4,17 7,56 | 3,32 5,39 | 2,92 4,51 | 2,69 4,02 | 2,53 3,70 | 2,42 3,47 | 2,34 3,30 | 2,27 3,17 | 2,21 3,06 | 2,16 2,98 | 2,12 2,90 | 2,09 2,84 | 2,04 2,74 | 1,99 2,66 | 1,93 2,55 | 1,89 2,47 | 1,84 2,38 |
|
|
|
|
|
|
