Нагрузки на насосные штанги и станок-качалку

При работе штанговой глубинной установки практическое значение имеют суммарные максимальные нагрузки на штанги. Эти нагрузки определяются с достаточно высокой точностью при помощи специального прибора - динамографа. В то же время необходимо уметь подсчитывать нагрузки на штанги. Основными суммарными нагрузками на штанги являются статические нагрузки. При ходе плунжера вверх штанги испытывают максимальную нагрузку от собственной силы тяжести и силы тяжести жидкости в трубах над плунжером. При движении вниз штанги испытывают лишь действие собственной силы тяжести. Таким образом, максимальные статические нагрузки будут при ходе вверх в точке подвеса штанг:

(103)

где Р_шт - сила тяжести штанг; Р_ж - масса жидкости над плунжером; g - ускорение свободного падения; Р_тр - силы трения штанг

о трубы и плунжера о стенки цилиндра насоса. Можно также написать уравнение (103) без учета разгружающей силы давления на плунжер снизу небольшого столба жидкости в межтрубном пространстве:

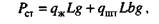
(104)

где д_ж - масса 1 м столба жидкости с поперечным сечением, равным сечению плунжера; g - ускорение свободного падения; q_w -масса 1 м штанг с муфтой; L - длина штанг; Ъ - коэффициент, учитывающий уменьшение массы штанг в жидкости, равный (/?! - р)1 р\; А^и Р ~ плотности материала штанг и жидкости.

С учетом сил трения фактические нагрузки будут несколько больше. В скважинах с кривизной 5-6° сила трения штанг о трубы составляет около 2% от силы тяжести штанг, и ею можно пренебречь.

Однако в наклонных и кривых скважинах силы трения могут быть более 2% от силы тяжести штанг, и пренебрегать ими нельзя.

Аналитически силы трения в наклонных и искривленных скважинах из-за многих неизвестных факторов, связанных со сложным профилем ствола скважины, определить трудно. Поэтому все расчеты максимальных нагрузок на штанги, проведенные без учета сил трения, верны только для вертикальных скважин и скважин с наклоном не более 5-6°. Силы инерции движущихся масс определяют следующим образом.

Согласно теории кривошипно-шатунного механизма, максимальное ускорение точки подвеса штанг будет вначале хода штанг вверх

(105)

где S - двойная амплитуда качаний головки балансира (длина хода полированного штока); г - радиус кривошипа; / - длина шатуна; (О - угловая скорость вращения кривошипа:

где п - число качаний балансира в минуту.

По найденной величине ускорения максимальную нагрузку от силы инерции определяют по формуле

(106)

где М - величина движущихся масс; У_тах - максимальное ускорение точки подвеса штанг.

С учетом сжимаемости жидкости величину инерции для нее можно не учитывать. Тогда инерционная нагрузка будет определяться в основном массой штанг:

(107)

где Р^ - масса штанг.

На практике отношение радиуса кривошипа г к длине шатуна 1 составляет от j^ до ^. При г/1 =)/₄ получим

(108)

где

- фактор динамичности.

С учетом сил инерции максимальная нагрузка на балансир в точке подвеса штанг при ходе вверх

(109)

где Рщ_Т - сила тяжести штанг в жидкости; 5, п - длина хода и число ходов сальникового (полированного) штока; Р_ж - масса жидкости над плунжером.

Формулой (109) можно пользоваться лишь для расчета неглубоких скважин, т.к. при больших глубинах и числе ходов возникают динамические нагрузки от вибрации штанг, которые на+ кладываются на инерционные усилия. Аналитически точно определить динамические нагрузки с учетом колебательных процес-* ' сов в штангах из-за сложности явлений трудно. Поэтому для pac-f четов многими исследователями предложены приближенные формулы А.С. Верновского, А.И. Адонина, И.А. Чарного, которые отличаются друг от друга различной оценкой фактора динамичности. В общем виде максимальную нагрузку на штанги при ходе вверх записывают как

3.10. Упругие деформации штанг и труб

Насосно-компрессорные трубы и штанги, находясь в скважине, испытывают нагрузку от своей массы и находятся в растянутом состоянии. В процессе работы штанговой насосной установки на трубы и штанги действуют силы тяжести столба жидкости.

При ходе плунжера вверх с момента начала движения точки подвеса штанг они начинают воспринимать нагрузку от жидкости, которая до этого действовала на трубы. По мере перевода нагрузки от труб на штанги они растягиваются, а трубы в это же время сокращаются. В начальный период движения штанг вверх плунжер остается неподвижным до тех пор, пока штанги не воспримут на себя всю нагрузку от жидкости. В этот период времени сумма упругих деформаций штанг и труб Я_ст будет равна величине перемещения точки подвеса штанг. Эта величина представляет собой потери хода плунжера при его движении вверх, так как плунжер не начал еще движение относительно втулок цилиндра насоса. Эти потери хода равны

где ij^j. и i - потери хода вследствие упругих деформаций, соответственно, штанг и труб. После того как вся статическая нагруз-

ка от жидкости будет воспринята штангами, начнется относительное перемещение плунжера и начинается подача жидкости насосом. После завершения хода плунжера вверх точка подвеса штанг начнет перемещаться вниз и упругие деформации будут происходить в обратном порядке. При ходе штанг вниз штанги разгружаются и нагрузка от штанг будет передаваться трубам. После полного восприятия нагрузки от жидкости начнется движение плунжера относительно втулок цилиндра насоса.

Следовательно, при движении плунжера вниз происходит потеря хода Д_ст, равная сумме величин упругих деформаций труб и штанг.

Д._т - суммарные потери хода плунжера от действия статической нагрузки.

В результате удлинения штанг и труб под действием статических нагрузок, которые определяются массой столба жидкости в НКТ и весом штанг и труб, действительный ход плунжера будет меньше хода точки подвеса штанг к балансиру на величи-^НУ ^ = ^г'0& На > ^тогда

(НО)

где 5_ПЛ - длина хода плунжера; S - длина хода точки подвеса штанг к балансиру; Я_ст - суммарные потери хода сальникового штока от действия статической нагрузки.

Чем больше нагрузка на верхнюю часть колонны труб и штанг, тем больше их удлинение.

Удлинение штанг и труб определяется на основе закона Гу-ка:

удлинение штанг

(111)

удлинение труб

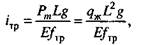
(112)

где L - длина штанг, м; Е - модуль упругости (для стали Е = 2,06-10 Па); /_шт - площадь поперечного сечения штанг, м²;

/jp - площадь поперечного сечения труб по металлу, м²; g - ускорение свободного падения (g = 9,81 м/с); q_m - масса 1 м столба жидкости, кг.

Суммарные потери хода сальникового штока за один цикл работы насоса составляют

(ИЗ)

Учитывая, что <?_ж = Fp, из (113) получим

(114)

где F - площадь поперечного сечения плунжера, м²; р - плотность жидкости, кг/м³.

Если трубы спущены с пакером, т.е. трубы не могут перемещаться в вертикальном положении, тогда уравнение (114) примет вид

(115)

При малых скоростях откачки (при п < 8) длину хода плунжера с достаточной точностью можно определить по формуле (110).

С увеличением скорости откачки на движение плунжера влияют и инерционные нагрузки от ускорения свободного падения штанг и их колебаний.

Когда плунжер движется вниз, инерционные силы продвигают плунжер несколько вниз уже после того, как головка балансира начала свое движение вверх.

Самостоятельное движение плунжера под действием сил инерции увеличивает длину хода плунжера в сравнении с ходом, который он имел при отсутствии динамических нагрузок. С учетом дополнительного движения плунжера под динамическими нагрузками длина хода плунжера определяется по формуле

(116)

где 5,- - увеличение длины хода плунжера за счет динамических нагрузок.

Учитывая (105),

(117)

где п - число ходов сальникового штока.

В этом случае длина хода плунжера определяется по формуле

(118)

где

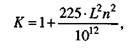
и называется фактором выигрыша хода, который можно определить по графику (рис. 93) длины хода плунжера.

⇐ Предыдущая28293031323334353637Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: