 |
Важнейшие примеры грамматик
|
|
|
|
ФОРМАЛЬНЫЕ ГРАММАТИКИ И ЯЗЫКИ
В литературе этот раздел информатики освящен по-разному (имеются монографии [11], [12] и др., а также главы в монографиях, например, [13], посвященные формальным грамматикам). Мы опишем иерархию Хомского и докажем ряд утверждений о рассматриваемых языках. В частности, будет изложено короткое (по сравнению с имеющимся в [11]) авторское доказательство неразрешимости проблемы грамматического разбора для грамматик типа 0. Также будет продемонстрирована связь между КС-языками и языками программирования высокого уровня. В заключение опишем класс так называемых аксиоматических грамматик, сочетающий в себе элементы исчислений.
ОСНОВНЫЕ ПОНЯТИЯ
В дальнейшем конечные множества символов называются алфавитами, а их элементы – буквами. Конечная последовательность букв (из данного алфавита) называется словом (в данном алфавите). Пустое слово обозначается через  (читается “ламбда”). Если А – алфавит, то множество всех слов в алфавите А обозначается через
(читается “ламбда”). Если А – алфавит, то множество всех слов в алфавите А обозначается через  (включая пустое слово), а
(включая пустое слово), а  есть
есть  без
без  .
.
ОПРЕДЕЛЕНИЕ 1. Порождающей грамматикой, или П-грамматикой, или грамматикой типа 0 называется упорядоченная четверка  , где V и W – непересекающиеся непустые конечные алфавиты, причем V – алфавит основных символов, а W – алфавит вспомогательных символов, J – начальный символ и
, где V и W – непересекающиеся непустые конечные алфавиты, причем V – алфавит основных символов, а W – алфавит вспомогательных символов, J – начальный символ и 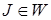 , а R – конечное множество слов вида
, а R – конечное множество слов вида  , называемых правилами, где
, называемых правилами, где 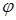 и
и  – различные слова в алфавите
– различные слова в алфавите  и
и  .
.
Пример 1.  есть П-грамматика.
есть П-грамматика.
Согласимся, что  есть
есть  (n раз,
(n раз,  ), а
), а  означает
означает  .
.
С учетом этих соглашений грамматика  запишется следующим образом:
запишется следующим образом:  .
.
Грамматика определяет язык рекурсивным образом. Рекурсивность проявляется в задании особого рода слов, называемых выводимыми словами грамматики.
|
|
|
ОПРЕДЕЛЕНИЕ 2. Индуктивное определение выводимых слов грамматики  .
.
1. J – выводимое слово этой грамматики.
2.  Если
Если  – выводимое слово грамматики
– выводимое слово грамматики 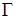 и правило
и правило  из R, то
из R, то  есть также выводимое слово; будем говорить, что слово
есть также выводимое слово; будем говорить, что слово  непосредственно выводимо из слова
непосредственно выводимо из слова  в грамматике
в грамматике 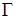 и писать
и писать 
 . Определение закончено, т. е. других правил построения выводимых слов нет.
. Определение закончено, т. е. других правил построения выводимых слов нет.
Пример 2. Слова  выводимы в
выводимы в  , причем последнее слово есть слово из основных символов.
, причем последнее слово есть слово из основных символов.
ОПРЕДЕЛЕНИЕ 3. Множество всевозможных слов из основных символов, выводимых в грамматике 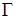 , называется языком, порождаемым грамматикой
, называется языком, порождаемым грамматикой 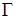 и обозначается через
и обозначается через  .
.
Пример 3.  .
.

 ОПРЕДЕЛЕНИЕ 4. Последовательность слов
ОПРЕДЕЛЕНИЕ 4. Последовательность слов  называется выводом слова
называется выводом слова  из слова
из слова  в грамматике
в грамматике 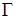 (символически
(символически 
 ), если для каждого
), если для каждого  выполнено
выполнено

 .
.
Теперь определение языка, порождаемого грамматикой  можно записать следующим образом:
можно записать следующим образом:
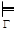
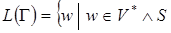
 .
.
Пример 4. Язык  , порождаемый грамматикой
, порождаемый грамматикой  состоит из всех десятичных записей натуральных чисел, включая
состоит из всех десятичных записей натуральных чисел, включая  ,
,  и др., т. е. возможны записи с незначащими нулями слева.
и др., т. е. возможны записи с незначащими нулями слева.
ОПРЕДЕЛЕНИЕ 5. П-грамматика  , каждое правило которой имеет вид
, каждое правило которой имеет вид  , где
, где  и
и 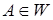 , называется грамматикой непосредственно составляющих, или НС-грамматикой, или грамматикой типа I; в правиле
, называется грамматикой непосредственно составляющих, или НС-грамматикой, или грамматикой типа I; в правиле  слова
слова  и
и  называются контекстами.
называются контекстами.
Пример 5. Грамматика 
 есть НС-грамматика. Можно доказать, что
есть НС-грамматика. Можно доказать, что  .
.
ОПРЕДЕЛЕНИЕ 6. П-грамматика  , каждое пра-вило которой имеет вид
, каждое пра-вило которой имеет вид  , где
, где 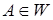 и
и  , называется контекстно-свободной, или КС-грамматикой, или грамматикой типа 2.
, называется контекстно-свободной, или КС-грамматикой, или грамматикой типа 2.
Подчеркнем, что в каждом правиле  из КС-грамматики
из КС-грамматики  . В выше приведенных примерах грамматики
. В выше приведенных примерах грамматики  и
и  были КС-грамматиками.
были КС-грамматиками.
Пример 6. а) Грамматика 
 есть КС-грамматика. Язык
есть КС-грамматика. Язык  состоит из всех слов с равным числом нулей и единиц.
состоит из всех слов с равным числом нулей и единиц.
b) Грамматика 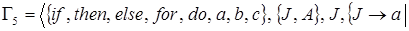
 также есть КС-грамматика.
также есть КС-грамматика.
ОПРЕДЕЛЕНИЕ 7. П-грамматика  , каждое правило которой вида
, каждое правило которой вида  или
или 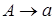 , где
, где  и
и  , называется автоматной, или А-грамматикой, или грамматикой
, называется автоматной, или А-грамматикой, или грамматикой
типа 3.
|
|
|
В примере 4 грамматика есть А-грамматика.
ОПРЕДЕЛЕНИЕ 8.Языки, порождаемые П-, НС-, КС-, и А-грамматиками называются соответственно П-, НС-, КС-, и А-языками.
Автоматные, КС-, НС- и П-грамматики образуют иерархию Хомского порождающих грамматик.
ВАЖНЕЙШИЕ ПРИМЕРЫ ГРАММАТИК
Во всех приводимых ниже примерах основные символы (буквы из основного алфавита) будут обозначаться строчными латинскими буквами или арабскими цифрами; вспомогательные символы (буквы из вспомогательного алфавита – заглавными латинскими буквами (все эти буквы могут быть с индексами)). Начальный символ всегда будем обозначать буквой J. Это позволит нам ограничиться выписыванием только множества правил приводимых грамматик.
Пример 1. а) Каждый непустой конечный язык  , где каждая буква
, где каждая буква  не является пустым символом, порождается А-грамматикой с правилами
не является пустым символом, порождается А-грамматикой с правилами  .
.
b) Каждый непустой конечный язык  , где
, где  , порождается А-грамматикой с множеством правил
, порождается А-грамматикой с множеством правил  .
.
с) Пустой язык  порождается А-грамматикой с правилом
порождается А-грамматикой с правилом  .
.
СЛЕДСТВИЕ 1. Каждый конечный язык, не содержащий пустого слова  , является А-языком.
, является А-языком.
Пример 2. Для каждого алфавита V язык  порождается А-грамматикой с множеством правил
порождается А-грамматикой с множеством правил  , в котором ровно
, в котором ровно 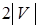 правил.
правил.
Пример 3. Язык  порождается А-грамматикой с правилами
порождается А-грамматикой с правилами  .
.
Пример 4. Языки
 и
и 
порождаются КС-грамматиками с множествами правил
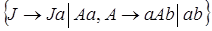 и
и 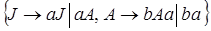
соответственно.
Если x и y – слова, то их умножением (или конкатенацией) называется слово xy, получаемое дописыванием к слову x справа слова y.
Умножением языков  и
и  (взятых именно в этом порядке) называется язык
(взятых именно в этом порядке) называется язык  .
.
|
|
|


