 |
Критическая длина волны и структура поля различных типов волн в волноводе
|
|
|
|
Критическая длина волны и структура поля различных типов волн в волноводе
Прямоугольные волноводы (рис. 10. 2)
Из решения волнового уравнения (10. 1) для поперечного волнового числа g следует
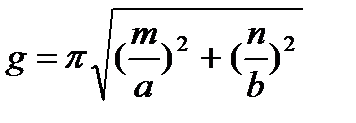
С учетом последнего соотношения критическая длина волны в волноводе
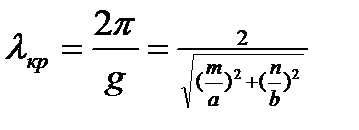
где а и b - размеры соответственно широкой и узкой стенок волновода.
Поперечные волновые числа g образуют бесконечный дискретный ряд в соответствии с величинами т и п. Каждому значению чисел т и п соответствует свой тип волны в волноводе, поэтому каждый из этих типов обозначается как волны типа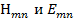 
. Индексы т и n показывают число полупериодов поля, укладывающихся между стенками волновода по осям x и у (рис. 10. 2, а); Волны типа 
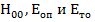не существуют, как неудовлетворяющие граничным условиям на стенках волновода.
Волна, имеющая наибольшую критическую длину волны, называется основной. Такой волной в прямоугольном волноводе является волна типа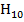 
, имеющая критическую длину волны 
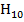. Все остальные типы волн (как Е, так и Н) называются высшими типами волн. Картина поля волны в продольном и поперечном сечениях волновода показана на рис. 10. 2, б. На этом же рисунке изображены силовые линии и показаны законы изменения составляющих полей по координатам х и у
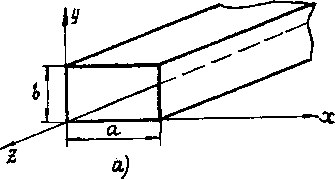
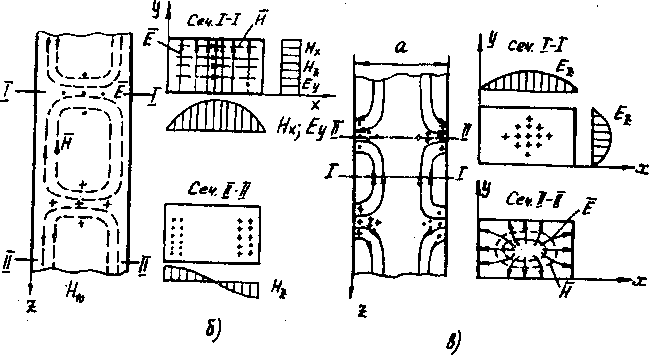
Рис. 10. 2. Прямоугольный волновод: a-выбор начала отсчета; б-картина поля волны типа H10 в прямоугольном волноводе; в-картина поля волны типа E11
Волна типа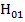 
имеет значение индексов m=0 и n=1, поэтому ее структура такая же, как и у волны типа 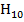, только оси х и у следует поменять местами ( 
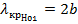). Простейшей из волн типа Е является волна E11 (рис. 10. 2, в).
Токи проводимости на стенках волновода
Для правильного конструирования и обеспечения соединения волноводов необходимо знать направление токов на стенках волновода и их величину. Величина и направление тока определяются из граничных условий электродинамики на поверхности идеального проводника:
|
|
|
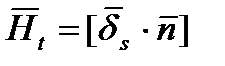
или (рис. 10. 3, а)
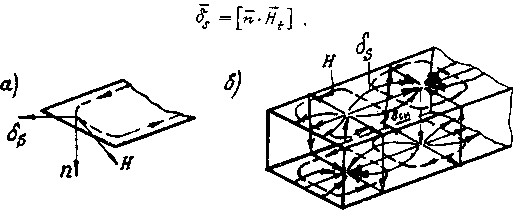
Рис. 10. 3. Поверхностные токи и ток смещения волны H10: a-к определению направления поверхностных токов проводимости; б-картина токов
Таким образом, поверхностный ток на стенках волновода перпендикулярен к касательной составляющей магнитного поля 
, а поверхностная плотность тока по величине равна касательной составляющей вектора напряженности магнитного поля (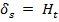 
). Направление токов определяется по правилу векторного произведения. Пример распределения поверхностных токов для волны типа 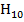в докритическом режиме в прямоугольном волноводе приведен на рис. 10. 3, б.
Круглые волноводы
Решение волнового уравнения, которое в данном случае удобнее всего проводить в цилиндрической системе координат (рис. 10. 4, а) показывает, что составляющие полей выражаются через функции Бесселя, а поперечные волновые числа принимают значения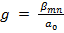 
Рис. 10. 4. Круглый волновод: a-выбор начала отсчета; б-картина поля волны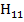 
в круглом волноводе; в-картина поля волны 
г-картина поля волны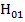
(для волн типа Е) и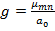 
(для волн типа Н). Отсюда
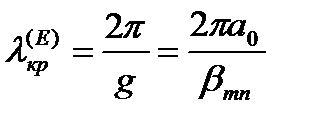и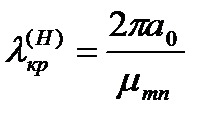 
где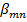 
- n-ый корень функции Бесселя m-го порядка;
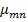- n-ый корень производной функции Бесселя m-го порядка
m - порядок функции Бесселя или количество периодов изменения поля вдоль окружности волновода;
п - номер корня (определяет число максимумов поля вдоль радиуса от середины до стенки волновода);
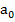- радиус волновода.
В зависимости от индексов m и п волны в круглых волноводах, так же как и в прямоугольных, обозначают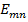 
и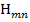 
. Волны с индексом п =0 ( 
, 
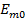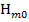) не существуют, так как их поля не удовлетворяют граничным условиям. Значения корня бесселевой функции или ее производной и значения 
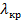некоторых типов колебаний приведены в табл. 10. 1.
|
|
|
Таблица 10. 1
| Тип колебаний Н или Е | Значение корня бесселевой функции или ее производно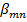й
или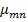
| Критическая длина волны
|
|
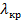
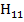
| 1, 841 | 3, 412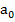
|
|
| 2, 405 | 2, 613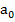
|
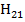
| 3, 054 | 2, 057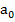
|
|
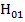
| 3, 832 | 1, 640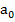
|
Из таблицы видно, что волна типа 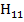имеет наибольшую критическую длину волны и является основной для круглого волновода. Картина поля волны 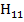показана на рис. 10. 4, б. В этой волне поляризация поля неустойчива. При прохождении волны
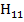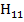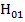через различные неоднородности (изгибы волновода, случайные деформации его сечения и др. ) плоскость поляризации волны может измениться, вследствие чего передача энергии нарушится. Поэтому волна не нашла широкого применения. Поля волн типа (рис. 10. 4, в) и (рис. 10. 4, г) обладают осевой симметрией, т. е. не зависят от угловой координаты α в плоскости поперечного сечения волновода.
П-и Н-образные волноводы
Волноводы с П-и Н-образными формами поперечного сечения получаются в результате постепенной деформации прямоугольного волновода. П-волновод образуется из прямоугольного волновода добавлением к последнему одного продольного металлического ребра, а Н-волновод - путем добавления двух ребер. Наличие ребер искажает поле волны 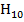в прямоугольном волноводе. На рис. 10. 5, а показаны поперечные сечения П-и Н-волноводов и картины силовых линий электрического поля в секущих плоскостях,
При передаче через П-или Н-волновод колебаний, соответствующих в прямоугольном волноводе виду 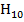, критическая длина волны увеличивается. За счет уменьшения зазора 
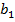в области продольного ребра 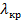может увеличиваться неограниченно. Критические длины высших типов волн значительно меньше зависят от величины зазора и увеличиваются мало, а это значит, что П-и Н-образные волноводы имеют увеличенную полосу пропускания.
Если соотношения геометрических размеров П-и Н-волноводов соответствуют показанным на рис. 10. 5, а, то их критические длины волн одинаковы.
Для определения критической длины волны П-и Н-образных волноводов используют графики, полученные Л. Н. Дерюгиным, показывающие зависимость фактора повышения критической длины волны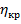 
от отношения высоты выступа к высоте волновода 
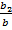для ряда фиксированных значений отношения ширины выступа к ширине волновода 
. Фактор повышения критической длины волны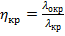 
показывает, во сколько раз критическая длина волны П-и Н-волноводов 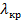больше критической длины волны 
прямоугольного волновода тех же размеров с основным типом колебаний. На рис. 10. 5, б приведена зависимость 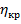от отношения 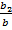для фиксированного значения 
.
|
|
|
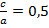Пример. Прямоугольный волновод с внутренними размерами 10x23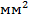 
имеет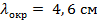 
. П-образный волновод тех же габаритов с 
, с = 5, 7 мм имеет 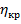= 0, 85 и 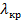= 5, 41 см.
Рис. 10. 5. П-и Н-волноводы: а-поперечное сечение волноводов; б-зависимость фактора η кр от размеров поперечного сечения П-волновода
Диэлектрические волноводы
В металлических волноводах с увеличением частоты из-за поверхностного эффекта возрастает поверхностное сопротивление проводников и потери увеличиваются. Поэтому обеспечение передачи электромагнитной энергии в диапазоне СВЧ на большие расстояния сложная задача. Одним из направлений в решении ее является использование замедленных поверхностных волн. Как известно, часть энергии замедленной поверхностной волны распространяется над волноводной структурой в свободном пространстве. Это свойство можно использовать для уменьшения потерь.
Типичными примерами использования замедленных поверхностных волн являются различные модификации диэлектрических волноводов, представляющих собой сплошные или полые диэлектрические стержни, вдоль которых распространяются электромагнитные волны путем отражения и преломления их на границе раздела диэлектрик - воздух (рис. 10. 6, а).
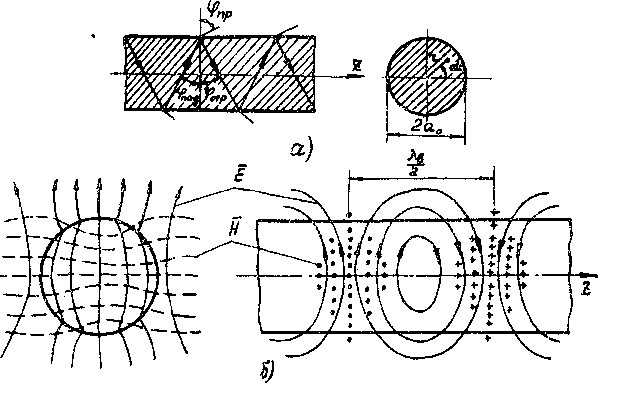
Рис. 10. б. Круглый диэлектрический стержень: а-отражение и преломление волн в нем; б-картина поля волны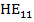 
Напомним, что в металлических волноводах образование волн типа Е и Н также связано с отражением волн от стенок волновода.
Отыскание поля в диэлектрическом волноводе сводится к решению волнового уравнения в цилиндрической системе координат. Это поле должно существовать внутри и вне стержня. Найденные выражения для полей должны при этом удовлетворять следующим условиям:
|
|
|
1) при r→ ∞, т. е. вне диэлектрического стержня, все компоненты поля должны стремиться к нулю;
2) внутри стержня (при r→ 0) поля нигде же обращаются в бесконечность;
3) касательные составляющие полей на границе раздела воздух - диэлектрик непрерывны.
Ввиду сложности решения (приходится пользоваться функциями Бесселя и Макдональда) остановимся на основных результатах теории диэлектрических волноводов.
Как известно, в металлических волноводах могут существовать независимо волны типа 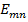и 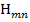. В диэлектрических волноводах несимметричные волны 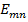и 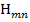не существуют раздельно, так как одна волна 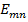или 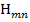не удовлетворяет граничным условиям. Следовательно, волны носят гибридный характер, т. е. имеют продольные составляющие как электрических, так и магнитных полей. Однако это положение не распространяется на азимутально симметричные волны 
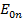и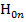 
, которые могут существовать самостоятельно в диэлектрическом стержне.
Исследование волнового уравнения показывает, что при индексе т ≠ 0 оно имеет две ветви решений, соответственно которым несимметричные волны принято делить на две группы.
Гибридные волны одной ветви решений, включающие основную волну, обозначают символами НЕ, а волны другой ветви – символами ЕН. Из двух гибридных волн с наименьшими индексам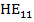и и 
основной, обладающей нулевой критической частотой, является только волна 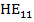; волна обладает конечной критической частотой.
Таким образом:
1) в диэлектрическом волноводе может существовать бесчисленное множество типов волн, имеющих различный характер изменения поля по координатам r; α;
2) каждый тип волны имеет свою критическую частоту; исключение составляет волна 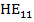, не имеющая критической частоты ( λ кр= ∞ );
3) фазовая скорость волны в диэлектрическом волноводе в зависимости от относительного радиуса стержня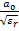 
меняется приблизительно от скорости света с в окружающем пространстве, до скорости света в заданной среде 
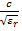, из которой выполнен диэлектрический стержень;
4) электромагнитная энергия в случае диэлектрического волновода переносится волнами как внутри, так и вне стержня; чем больше отношение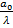 
при данной длине волны, тем большая часть энергии переносится внутри стержня.
Следует отметить, что равенство нулю критических частот основных волн диэлектрических волноводов любой формы поперечного сечения не означает, что волны в диэлектрических волноводах практически существуют на сколь угодно низких частотах. Это связано с тем, что направляющее действие и степень концентрации энергии в диэлектрическом волноводе быстро уменьшаются при снижении частоты ниже некоторого значения, называемого реальной критической частотой. Таким образом, можно сказать, что критическая частота основных волн диэлектрических волноводов является менее четко определенной, чем, например, полых металлических волноводов.
|
|
|
Картина ноля основной волны круглого диэлектрического волновода 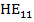показана на рис. 10. 6, б.
|
|
|
