 |
Лабораторная работа 4. Проверка статистических гипотез
|
|
|
|
Построение критической области
Методика проверки нулевой гипотезы основанному на заключении теоремы Гливенко, согласно которой
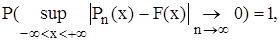
где  эмпирическая функция распределения.
эмпирическая функция распределения.
Эмпирическая функция распределения определяется так:
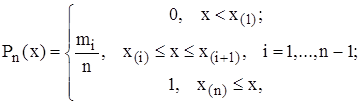 (15)
(15)
где  количество элементов
количество элементов  вариационного ряда
вариационного ряда 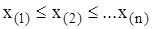 данной выборки, не крупнее
данной выборки, не крупнее 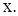
Исходная статистика критерия Колмогорова определяется как максимум отклонения эмпирического распределения 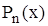 (определяется по выборке) от гипотетической функции распределения F (x). Она имеет вид
(определяется по выборке) от гипотетической функции распределения F (x). Она имеет вид
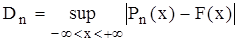 , (16)
, (16)
где 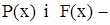 в соответствии эмпирическая и теоретическая функции распределения.
в соответствии эмпирическая и теоретическая функции распределения.
Исходная статистика 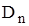 вычисляется следующим образом. Вычисляются так называемые кумулятивные разницы
вычисляется следующим образом. Вычисляются так называемые кумулятивные разницы
 (17)
(17)
Далее вычисляется исходная статистика
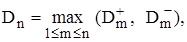 (18)
(18)
или иначе
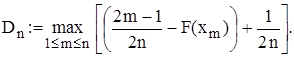
При истинности гипотезы  статистика
статистика 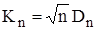 имеет так называемый распределение Колмогорова, независимый от гипотетической функции распределения
имеет так называемый распределение Колмогорова, независимый от гипотетической функции распределения 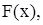 который при
который при 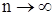 совпадает с распределением
совпадает с распределением
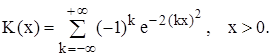 (19)
(19)
Статистика 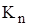 называется статистикой Колмогорова.
называется статистикой Колмогорова.
Критическое значение критерия  находится как квантиль порядка
находится как квантиль порядка 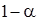 этого распределения.
этого распределения.
Для нахождения квантилей распределения Колмогорова существуют специальные таблицы, которые приведены во многих книгах по математической статистике.
При 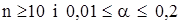 можно воспользоваться приближенной формулой для вычисления
можно воспользоваться приближенной формулой для вычисления 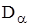 :
:
 . (20)
. (20)
Алгоритм проверки гипотезы
1. По заданной выборке 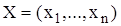 определяется вариационный ряд
определяется вариационный ряд 
2. Определяется эмпирическая функция распределения 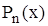 и гипотетическая теоретическая функция распределения
и гипотетическая теоретическая функция распределения 
3. Определяется степень различия между теоретическим и эмпирическим распределением 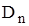 по формуле (17).
по формуле (17).
4. Задается уровень значимости  и из соотношения
и из соотношения
|
|
|
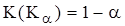
находится соответствующее критическое значение статистики  как квантиль порядка
как квантиль порядка  распределения Колмогорова.
распределения Колмогорова.
5. Сравниваются значения 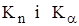 . Если
. Если  , то гипотеза
, то гипотеза 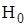 о том, что случайная величина Х имеет заданный закон распределения, принимается, в противном случае гипотеза
о том, что случайная величина Х имеет заданный закон распределения, принимается, в противном случае гипотеза 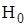 отклоняется, то есть гипотеза
отклоняется, то есть гипотеза 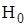 противоречит выборочным данным.
противоречит выборочным данным.
6. Сравниваются значения 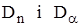 . Для вычисления критического значения
. Для вычисления критического значения 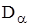 можно пользоваться формулой (6). Гипотеза
можно пользоваться формулой (6). Гипотеза 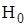 принимается, если
принимается, если 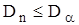 , в противном случае гипотеза
, в противном случае гипотеза 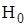 отвергается.
отвергается.
Лабораторная работа 4. Проверка статистических гипотез
1. Проверка гипотезы  о равенстве математического ожидания заданному значению.
о равенстве математического ожидания заданному значению.
Пример 1. Завод производит стальные тросы, прочность на розрив которых случайная величина, распределенная по нормальному закону с параметрами 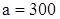 кгс,
кгс, 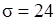 кгс. Предполагают, что некоторое усовершенствование технологии производства тросов позволит увеличить их прочность.
кгс. Предполагают, что некоторое усовершенствование технологии производства тросов позволит увеличить их прочность.
1. Выработать правило принятия решения для внедрения новой технологии, принимая уровень значимости  если испытаны на прочность 64 тросы.
если испытаны на прочность 64 тросы.
2. В условиях принятого правила вычислить вероятность сохранить старую технологию в производстве тросов, если в действительности новая технология позволяет увеличить среднюю прочность на разрыв тросов к  кгс, предполагая, что среднее квадратическое отклонение остается равным
кгс, предполагая, что среднее квадратическое отклонение остается равным 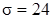 кгс.
кгс.
Решение. Если m является средняя прочность тросов на разрыв, тогда необходимо выбрать одну из двух гипотез: 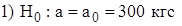 - новая технология не увеличивает прочность тросов;
- новая технология не увеличивает прочность тросов; 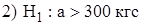 - новая технология является лучшей по сравнению со старой.
- новая технология является лучшей по сравнению со старой.
1. В данном случае исходная статистика равна 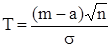 , T ~
, T ~ 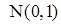 (нормально распределенная случайная величина с параметрами
(нормально распределенная случайная величина с параметрами 
2. При заданном уровне значимости 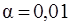 находим величину
находим величину 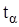 , при которой
, при которой 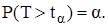
С этого условия находим  . Откуда
. Откуда 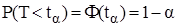 , где
, где 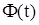 - функция распределения нормированного нормального распределения. Величину
- функция распределения нормированного нормального распределения. Величину 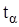 находим как квантиль распределения
находим как квантиль распределения 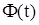 порядка
порядка  .
.
|
|
|
3. Формулируем правило принятия гипотезы: если 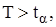 есть
есть 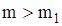 , где
, где  необходимо отклонить гипотезу и принять ее, если
необходимо отклонить гипотезу и принять ее, если 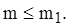
Иными словами, новая технология будет принята, если средняя прочность испытанных тросов будет больше  кгс, и отклонена в противном случае.
кгс, и отклонена в противном случае.
Алгоритм в Mathcad
Исходные данные
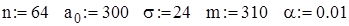
1. Определяет правило принятия решения для внедрения новой технологии, принимая уровень значимости 
Определяем квантиль уровня 
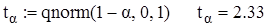
Вычисляем наблюдаемое значение критерия
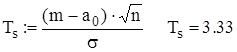
Верхняя граница прочности тросов, которая соответствует критической точке 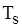

Проверка правила принятия гипотезы
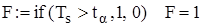
Значение критерия Т попадает в критическую область  , следовательно, гипотезу
, следовательно, гипотезу 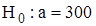 надо отклонить и принять гипотезу
надо отклонить и принять гипотезу  .
.
2. Определим теперь вероятность сохранения старой технологии. Рассмотрим две гипотезы (основную и альтернативную):
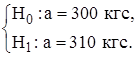
Вероятность сохранить старую технологию в производстве тросов, если действительно новая технология увеличивает среднюю прочность к 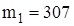 кгс, то есть вероятность ошибки 2-го рода равна
кгс, то есть вероятность ошибки 2-го рода равна
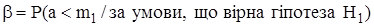 =
= 
Определим нормированную величину  с параметрами
с параметрами 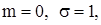 Используя функцию Mathcad
Используя функцию Mathcad 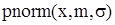 , которая определяет вероятность нормального распределения в точке х, получим
, которая определяет вероятность нормального распределения в точке х, получим
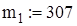

Таким образом, вероятность сохранить старую технологию производства тросов равна 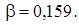 Мощность критерия
Мощность критерия 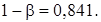 ◄
◄
2. Проверка гипотезы  о величине дисперсии нормального распределения. С нормальной генеральной совокупности с известной дисперсией
о величине дисперсии нормального распределения. С нормальной генеральной совокупности с известной дисперсией  добытая выборка объема
добытая выборка объема 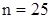 . Проверим при уровне значимости
. Проверим при уровне значимости 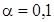 нулевую гипотезу
нулевую гипотезу 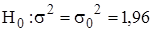 , приняв в качестве конкурирующей гипотезы
, приняв в качестве конкурирующей гипотезы 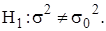
Алгоритм в Mathcad
Моделируем выборку объема с нормальным распределением 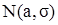
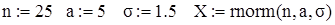
Фрагмент выборки

Точечные оценки математического ожидания и дисперсии генеральной совокупности
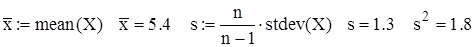
Гипотетическое значение дисперсии 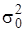 и уровень значимости
и уровень значимости 
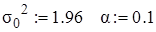
Исходная статистика
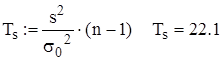
Квантили порядка  и
и 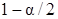 распределения
распределения 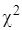 с
с 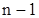 степенями свободы
степенями свободы 
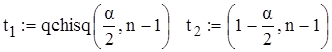
Область принятия гипотезы
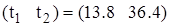
Проверяем условие попадания критерия Ts в область принятия гипотезы
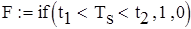
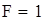
Значение критерия Ts попадает в область принятия гипотезы (F = 1), следовательно, гипотеза 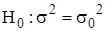 принимается. Альтернативная гипотеза
принимается. Альтернативная гипотеза  отклоняется.
отклоняется.
На практике рассматриваемая гипотеза проверяется, если нужно проверить точность приборов, инструментов, станков, методов исследования и постоянство технологических процессов. Например, если известна допустимая характеристика рассеяния контролируемого размера деталей, которые изготавливаются станком- автоматом, равна  а найденная по выборке окажется значу что больше
а найденная по выборке окажется значу что больше  то станок требует переналадки.
то станок требует переналадки.
|
|
|
3. Проверка гипотезы о нормальном распределении. Пусть исследуется непрерывная случайная величина Х - время заправки топливом автомобилей на автозаправочной станции (АЗС). Предположим, что гипотетический распределение величины Х нормальный. Надо проверить гипотезу о нормальном распределении величины Х по выборочным данным.
Решение. Получим выборку 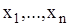 объема n с генеральной совокупности X - определяющая время заправок топливом автомобилей на АЗС.
объема n с генеральной совокупности X - определяющая время заправок топливом автомобилей на АЗС.
Проверка гипотезы о нормальном распределении проводится по общим алгоритмом проверки гипотез для непрерывных распределений.
Алгоритм в Mathcad
Генерируем выборку объема n = 100 с генеральной совокупности, распределенной по нормальному закону с параметрами m i σ и упорядочивая ее по росту, получаем вариационный ряд А:

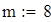
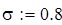
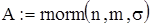
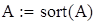

Определяем минимальное и максимальное значение вариационного ряда
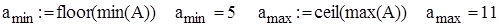
Рассчитывая размах выборки R и задавая количество интервалов группировки выборки k, получаем сгруппирован интервальный вариационный ряд с границами, представленными в массиве а:
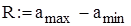

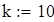
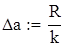

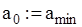

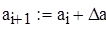

Применяя функцию Mathcad, получаем частотное распределение выборки Р:



По данным выборки находим числовые характеристики нормального распределения. Нормальное распределение определяется двумя параметрами – математическим ожиданием α и средним квадратическим отклонением σ. Их статистическим оценкам является среднее арифметическое m и среднее квадратическое отклонение σ. Вычисляем эти характеристики, принимая первоначальную выборку.
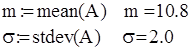
Определяем теоретические частоты (вероятности) нормального распределения с определенными параметрами m i σ. В соответствии с методикой определения теоретических частот нормального распределения расширим границы первого и последнего интервалов, положив
|
|
|
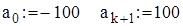
Для вычисления теоретических относительных частот Fi в Mathcad, применяем выражение
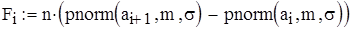
где pnorm (x, m, σ) - функция нормального распределения с параметрами m i σ.

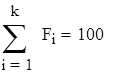
Уровень значимости и количество степеней свободы 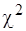
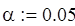
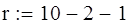

Наблюдаемое 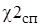 и критическое
и критическое 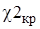 значение критерия
значение критерия
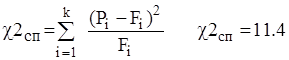
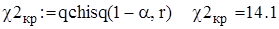
Применяем правило проверки статистических гипотез
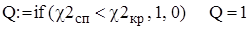
Поскольку неравенство 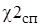 <
< 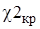 выполняется (Q = 1), то гипотеза о том, что генеральная совокупность распределена по нормальному закону не противоречит выборочным данным.
выполняется (Q = 1), то гипотеза о том, что генеральная совокупность распределена по нормальному закону не противоречит выборочным данным.
Строим графики эмпирического и теоретического распределений (рис. 2). Теоретическое распределение определяем по формуле 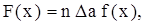 где f (x) - плотность нормального распределения с параметрами m i σ, для вычисления которой в Mathcad используется функция dnorm (x, m, σ). F (x) вычисляется по выражению
где f (x) - плотность нормального распределения с параметрами m i σ, для вычисления которой в Mathcad используется функция dnorm (x, m, σ). F (x) вычисляется по выражению
F (x) = n Δa qnorm (x, m, σ)
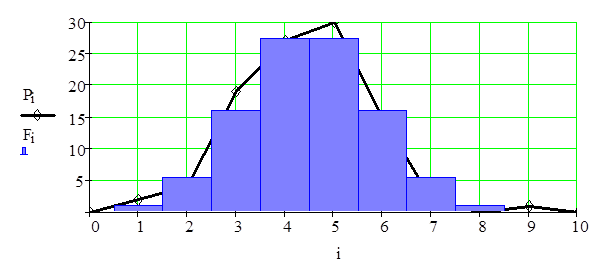
Рис. 2. График эмпирического С и теоретического F распределений◄
4. Проверка гипотезы о нормальном распределении по критерию Колмогорова. Пусть исследуется непрерывная случайная величина 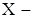 отклонения от графика времени прибытия автобусов на автостанцию. Предположим, что гипотетический распределение величины Х нормальный при уровне значимости
отклонения от графика времени прибытия автобусов на автостанцию. Предположим, что гипотетический распределение величины Х нормальный при уровне значимости 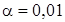 . Надо проверить гипотезу о нормальном распределении величины Х по выборочным данным по критерию Колмогорова.
. Надо проверить гипотезу о нормальном распределении величины Х по выборочным данным по критерию Колмогорова.
Решение. Получим выборку 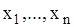 объема n с генеральной совокупности X, которая определяет отклонения от графика времени прибытия автобусов на автостанцию. Расчеты проводим по общему алгоритму проверки гипотез для непрерывных распределений.
объема n с генеральной совокупности X, которая определяет отклонения от графика времени прибытия автобусов на автостанцию. Расчеты проводим по общему алгоритму проверки гипотез для непрерывных распределений.
Алгоритм в Mathcad
Исходные данные



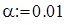
Генерирование выборки и определение вариационного ряда

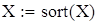
Фрагмент вариационного ряда

Функция нормального распределения
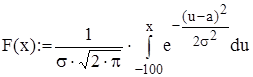
или функцией Mathcad
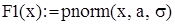
|
|
|


