Базовые циклы криптографических преобразований.

Как отмечено в начале настоящей статьи, ГОСТ относится к классу блочных шифров, то есть единицей обработки информации в нем является блок данных. Следовательно, вполне логично ожидать, что в нем будут определены алгоритмы для криптографических преобразований, то есть для зашифрования, расшифрования и «учета» в контрольной комбинации одного блока данных. Именно эти алгоритмы и называются базовыми циклами ГОСТа, что подчеркивает их фундаментальное значение для построения этого шифра.

Базовые циклы построены из основных шагов криптографического преобразования, рассмотренного в предыдущем разделе. В процессе выполнения основного шага используется только один элемент ключа, в то время как ключ ГОСТ содержит восемь таких элементов. Следовательно, чтобы ключ был использован полностью, каждый из базовых циклов должен многократно выполнять основной шаг с различными его элементами. Вместе с тем кажется вполне естественным, что в каждом базовом цикле все элементы ключа должны быть использованы одинаковое число раз, по соображениям стойкости шифра это число должно быть больше одного.

Все сделанные выше предположения, опирающиеся просто на здравый смысл, оказались верными. Базовые циклы заключаются в многократном выполнении основного шага с использованием разных элементов ключа и отличаются друг от друга только числом повторения шага и порядком использования ключевых элементов. Ниже приведен этот порядок для различных циклов.

1. Цикл зашифрования 32-З:

K ₀, K ₁, K ₂, K ₃, K ₄, K ₅, K ₆, K ₇, K ₀, K ₁, K ₂, K ₃, K ₄, K ₅, K ₆, K ₇, K ₀, K ₁, K ₂, K ₃, K ₄, K ₅, K ₆, K ₇, K ₇, K ₆, K ₅, K ₄, K ₃, K ₂, K ₁, K ₀.

2. Цикл расшифрования 32-Р:

K ₀, K ₁, K ₂, K ₃, K ₄, K ₅, K ₆, K ₇, K ₇, K ₆, K ₅, K ₄, K ₃, K ₂, K ₁, K ₀, K ₇, K ₆, K ₅, K ₄, K ₃, K ₂, K ₁, K ₀, K ₇, K ₆, K ₅, K ₄, K ₃, K ₂, K ₁, K ₀.

3. Цикл выработки имитовставки 16-З:

K ₀, K ₁, K ₂, K ₃, K ₄, K ₅, K ₆, K ₇, K ₀, K ₁, K ₂, K ₃, K ₄, K ₅, K ₆, K ₇.

Каждый из циклов имеет собственное буквенно-цифровое обозначение, соответствующее шаблону «n-X», где первый элемент обозначения (n), задает число повторений основного шага в цикле, а второй элемент обозначения (X), буква, задает порядок зашифрования («З») или расшифрования («Р») в использовании ключевых элементов. Этот порядок нуждается в дополнительном пояснении:

Цикл расшифрования должен быть обратным циклу зашифрования, то есть последовательное применение этих двух циклов к произвольному блоку должно дать в итоге исходный блок, что отражается следующим соотношением: Ц _32-Р (Ц _32-З (T)) = T, где T – произвольный 64-битный блок данных, Ц _X (T) – результат выполнения цикла X над блоком данных T. Для выполнения этого условия для алгоритмов, подобных ГОСТу, необходимо и достаточно, чтобы порядок использования ключевых элементов соответствующими циклами был взаимно обратным. В справедливости записанного условия для рассматриваемого случая легко убедиться, сравнив приведенные выше последовательности для циклов 32-З и 32-Р. Из сказанного вытекает одно интересное следствие: свойство цикла быть обратным другому циклу является взаимным, то есть цикл 32-З является обратным по отношению к циклу 32-Р. Другими словами, зашифрование блока данных теоретически может быть выполнено с помощью цикла расшифрования, в этом случае расшифрование блока данных должно быть выполнено циклом зашифрования. Из двух взаимно обратных циклов любой может быть использован для зашифрования, тогда второй должен быть использован для расшифрования данных, однако стандарт ГОСТ28147-89 закрепляет роли за циклами и не предоставляет пользователю права выбора в этом вопросе.

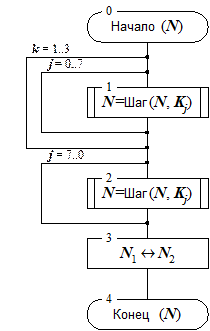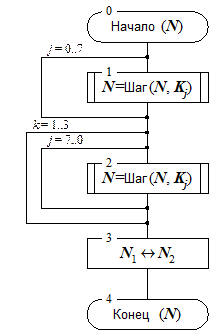Рис. 2а. Схема цикла зашифрования 32-З. Рис. 2б. Схема цикла расшифрования 32-Р.

Цикл выработки имитовставки вдвое короче циклов шифрования, порядок использования ключевых элементов в нем такой же, как в первых 16 шагах цикла зашифрования, в чем нетрудно убедиться, рассмотрев приведенные выше последовательности, поэтому этот порядок в обозначении цикла кодируется той же самой буквой «З».

Рис. 2в. Схема цикла выработки имитовставки 16-З.

Схемы базовых циклов приведены на рисунках 2а-в. Каждый из них принимает в качестве аргумента и возвращает в качестве результата 64-битный блок данных, обозначенный на схемах N. Символ Шаг(N, X) обозначает выполнение основного шага криптопреобразования для блока N с использованием ключевого элемента X. Между циклами шифрования и вычисления имитовставки есть еще одно отличие, не упомянутое выше: в конце базовых циклов шифрования старшая и младшая часть блока результата меняются местами, это необходимо для их взаимной обратимости.

 

ЗАДАНИЕ

Разработать консольную программу, выполняющую шифрование и дешифрование файлов, основываясь на параметрах командной строки. Для выбора варианта задания использовать приведённую ниже таблицу.

ВАРИАНТЫ

№ по журналу	С начальной и конечной перестановками	С поддержкой работы с файлами произвольного размера	Тип ключа: число или кодовая фраза
	Нет	Нет	Число
	Нет	Нет	Кодовая фраза
	Нет	Да	Число
	Нет	Да	Кодовая фраза
	Да	Нет	Число
	Да	Нет	Кодовая фраза
	Да	Да	Число
	Да	Да	Кодовая фраза
	Нет	Нет	Число
	Нет	Нет	Кодовая фраза
	Нет	Да	Число
	Нет	Да	Кодовая фраза
	Да	Нет	Число
	Да	Нет	Кодовая фраза
	Да	Да	Число
	Да	Да	Кодовая фраза
	Нет	Нет	Число
	Нет	Нет	Кодовая фраза
	Нет	Да	Число
	Нет	Да	Кодовая фраза
	Да	Нет	Число
	Да	Нет	Кодовая фраза
	Да	Да	Число
	Да	Да	Кодовая фраза
	Нет	Нет	Число
	Нет	Нет	Кодовая фраза
	Нет	Да	Число
	Нет	Да	Кодовая фраза
	Да	Нет	Число
	Да	Нет	Кодовая фраза
	Да	Да	Число
	Да	Да	Кодовая фраза

 

Пояснения:

4. С начальной и конечной перестановками

Алгоритм может применятся как с этими перестановками так и без, т.к. основная их цель перестановка бит удобным для аппаратной обработки образом.

5. С поддержкой работы с файлами произвольного размера

Варианты с такой поддержкой должны корректно обрабатывать файлы любого размера. В то время как варианты без неё должны уметь корректно работать только с файлами, размер которых кратен 8 байт.

6. Тип ключа: число или кодовая фраза

В случае числового ключа, в командной строке должно задаваться именно число (система счисления роли не играет). Для кодовой фразы перед использованием её в качестве ключа следует применить над ней некоторую функцию, которая преобразует её в 64-битовое число.

МОДУЛЬ 3. СТОЙКОСТЬ КРИПТОГРАФИЧЕСКИХ СИСТЕМ И АЛГОРИТМОВ.

Лабораторная работа № 4

«Разработка криптосистемы на основе ассиметричного алгоритма RSA с открытым ключом»
ЧАСть 1.

 

Цель работы: Ознакомление с базовыми принципами криптосистемы RSA.

 

Введение

Криптосистемы с открытым ключом позволяют обмениваться секретными сообщениями по открытому каналу, не договариваясь заранее о ключе шифра; даже перехватив весь разговор от начала до конца, враг (или, как говорят, «противник») не узнает секретного сообщения. Кроме того, эти же методы позволяют добавлять к сообщению «цифровую подпись», удостоверяющую, что сообщение не фальсифицировано врагами. Проверить аутентичность подписи легко, а подделать сё крайне трудно. Понятно, что такие методы находят широкое применение в банках, при подписывании контрактов, при денежных переводах.

Криптосистема RSA

 

Чтобы построить пару ключей для криптосистемы RSA (RSA cryptosystem), надо сделать следующее.

1. Взять два больших простых числа р и q (скажем, около 100 десятичных цифр в каждом).

2. Вычислить п = pq.

3. Взять небольшое нечётное число е, взаимно простое с (n). (Из соотношения следует, что (n) = (р - 1)(q - 1).)

4. Вычислить d = е^-1 mod (n). (d существует и определено однозначно по модулю (n).)

5. Составить пару Р = (е,п) — открытый RSA-ключ (RSA public key).

6. Составить пару S= (d,n)— секретный RSA-ключ (RSA secret key).

Множеством D всех возможных сообщений для этой криптосистемы явля­ется Открытому ключу Р= (е, п) соответствует преобразование

Р(М) = М^е mod n

а секретному ключу S = (d, п) — преобразование

S(C)= C^е mod n

Как уже говорилось, эти преобразования можно использовать и для шифрования, и для электронных подписей.

Проверка чисел на простоту

В этом разделе мы обсуждаем вопрос о том, как искать большие простые числа.

Распределение простых чисел

Как найти большое простое число? Естественный подход таков: взять боль­шое случайное число и посмотреть, не окажется ли оно простым. Если нет, попробовать другое случайное число и так далее. Этот способ пригоден, лишь если простые числа не слишком редки — к счастью, это действительно так, как показывает теорема о распределении простых чисел, доказанная в конце прошлого века. Вот её формулировка.

Определим функцию распределения простых чисел (prime distribution func­tion) , положив (п) равным количеству простых чисел, не превосходящих п. Например, на отрезке от 1 до 10 есть 4 простых числа 2, 3. 5 и 7, поэтому (10) = 4.

 

 

Асимптотический закон распределения простых чисел.

Выражение n/ln n даёт неплохое приближение к (п) даже при небольших значениях п. Уже при п= 10⁹ (небольшое число с точки зрения специалистов по теории чисел) погрешность приближения не превосходит 6% ( (10⁹) = 50 847 534, 10⁹/ln 10⁹ 48 254 942).

Асимптотический закон позволяет оценить вероятность, с которой целое число, наугад выбранное из отрезка от 1 до п, является простым - это примерно 1/ln n. Тем самым для отыскания простого числа от 1 до п нужно проверить на простоту порядка ln n случайно выбранных чисел. Например, чтобы найти простое число из 100 десятичных знаков, надо перебрать порядка ln 10¹⁰⁰ 230 случайных чисел от 1 до 10¹⁰⁰. (Эта оценка по очевидным причинам может быть уменьшена вдвое: проверять на простоту стоит только нечётные числа. Заметим также, что число десятичных знаков в наугад взятом числе от 1 до 10¹⁰⁰ с большой вероятностью близко к 100—около 90% всех чисел в этом диапазоне имеют 100 знаков, около 99%--99 или более знаков, около 99,9% — 98 или более знаков и т.д.)

Нам остаётся объяснить, каким образом можно проверить, будет ли про­стым данное большое число п. Другими словами, мы хотим узнать, состоит ли разложение числа п на простые множители

п =

(r 1; числа р₁,р₂,...,р_r— различные простые делители n) из единственного простого числа (r = 1, е₁ = 1).

Самый простой способ проверки — перебор делителей (trial division). Бу­дем пытаться разделить п на 2,3,..., (чётные числа, большие 2, можно пропускать). Если п не делится ни на одно из этих чисел, то оно простое (если п разлагается в произведение двух или более множителей, то один из множителей не превосходит ). Но дело это долгое — уже число делений есть (), и время работы экспоненциально зависит от длины записи числа п (напомним, что двоичное представление п занимает = [log(n + 1)] битов, так что = ()). Таким образом, такой подход применим, лишь есть число п мало или имеет небольшой делитель.

Если при переборе делителей мы обнаруживаем, что число п составное, то одновременно находится и делитель числа п. Для других способов проверки простоты это не так— можно убедиться, что число составное, так и не указав никакого его делителя. Это не удивительно, так как задача разложения числа на множители, по-видимому, гораздо сложнее задачи проверки простоты. К задаче разложения на множители мы вернёмся в следующем разделе.

МОДУЛЬ 4. КРИПТОСИСТЕМЫ С ОТКРЫТЫМ КЛЮЧОМ.

Лабораторная работа № 5

«Разработка криптосистемы на основе ассиметричного алгоритма RSA открытым ключом»
ЧАСть 2.

 

Псевдопростые числа

Сейчас мы опишем «почти правильный» алгоритм проверки числа на просто­ту, приемлемый для многих практических приложений. (Небольшое усложнение этого алгоритма, делающее его совсем правильным, будет описано дальше.)

Обозначим через множество всех ненулевых вычетов по модулю п:

Если число n, простое, то =

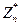
Назовем число п псевдопростым по основанию a (base-a pseudoprime), если выполнено утверждение малой теоремы Ферма:

а^n-1 1 (mod п). (1.42)

 

Любое простое число п является пссвдопростым по любому основанию a . Поэтому если нам удалось найти основание а., по которому п не является псев­допростым, то мы можем быть уверены, что п— составное. Оказывается, что во многих случаях достаточно проверить основание а =2.

PseudoPRIME(n)

1 if Modular-Exponentiation(2, n - 1,n) 1 (mod n)

2 then return COMPOSITE Заведомо.

3 else return PRIME Возможно.

Эта процедура может совершать ошибки, но только в одну сторону. Если она сообщает, что число п составное, то это действительно так, но она может принять составное число за простое (если оно является псевдопростым по осно­ванию 2). Как часто такое происходит? Оказывается, не так уж часто — среди чисел до 10000 есть только 22 числа, для которых процедура Pseudoprime даёт неверный ответ (первые четыре из них — 341, 561, 645 и 1105). Можно показать, что доля таких «плохих» чисел среди -значных чисел стремится к 0 при . Используя некоторые оценки, можно показать, что доля составных чисел среди 50-разрядных псевдопростых по основанию 2 чисел не превосходит 10^-6, а среди 100-разрядных псевдопростых чисел—10^-13.

 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: