 |
Параграф 8 - класс-контейнер (справочник 642)
|
|
|
|
классы-контейнеры - классы проектируемые для хранения коллекций (наборов) объектов определенных типов данных.
проектируем их в виде шаблонов
типы:
1)vector – динамический массив
2) list, linuted list - односвязные и двусвязные списки (справочник 646)
3) бинарные деревья (binary trees) - эфф сортировка,эфф поиск бинарный,
4) хэш таблицы - опимизированная для вставки и поиска элементов,
5) stack - стек
каждый контейнер должен предусматривать вставку, удаление, сортировку и поиск элементов. Каждый контейнер специализируется - преимущество в определенной задаче.
1) Векторы – динамические массивы, элементы хранятся последовательно в ячейках. Неэффективны вставка и удаление, эффективна сортировка
класс можно описать как вложенный класс - он будет объектом объемлющего класса.
vector - объемлющий
iterator - вложенный
class A
{
private: int x;
privat:double get_b();
class B{
}
...
}
методы класса А не имеют доступа в privat часть класса В
методы класса В не имеют доступа в privat часть класса А
в зависимости от того, где мы объявляем
в паблик - может создать и использовать объек класса В (чаще всего объявляем тут)
в приват - не можем
A::B obj - имя класса!
}
если требуется чтобы методу А требуется доступ в приват В то, class B{ friend class A...}
смотрим primer.cpp
2) односвязные списки - контейнер состоящий из набора узлов, где каждый узел содержит 2 элемента: элемент данных и ссылка на следующий (адрес следующего узла списка).
(эффективна вставка элемента и удаление, сортировка и поиск - неэффективны)
Списки:
а) Замкнутые (Циклические) – в конце ссылка на первый элемент
b) Незамкнутые – в конце NULL (нулевая ссылка)
Фиктивный узел – следующий за последним (он же пустышка)
|
|
|
преимущества структуры - гибкость по отношении к вставке, удалению элемента (сортировка - в векторе, а не тут) отличие списков от вектора- элементы списка могут быть разбросаны в памяти как угодно (это гуд!) для того чтобы найти итый элемент надо пройти весь путь от первого до нужного (поиск циклом)
псевдокод:
stract Node { Item data(данные), Node* next (ссылка);}
Note new_node (data);
new_node->next=x->next; //вставка типа
x-> next = &new_node;
//удаление
x-> next= x->next->next;
node * tmp = x-> next;
delete tmp;
node* x;
//поиск в списке
for (node* x!= begin x!=NULL; x= x-> next;
if (x-> data == key)
break;
BST – binary search tree (узлы имеют не более двух потомков)
http://algolist.manual.ru/ds/btree.php
BST – структурированная коллекция узлов, которые удовлетворяют правилу:
Значение в каждом узле левого поддерева должно быть меньше значения главного узла, и больше для правого узла.

А – корень,
В – левый потомок А
С – правый потомок А
В – корень левого поддерева А
Квадраты - листья
Размер – число внутренних узлов (в кружках)
Предок (родитель) узла p называется узел n, такой, что p – потомок узла n
Длина пути – число ребер между узлами.
Уровни: А – нулевой уровень,
B, C – первый уровень и т.д.
В зависимости от порядка на одинаковых наборах будут получаться разные деревья.
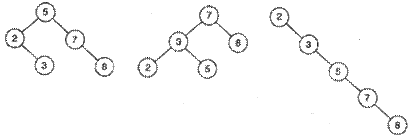
1) 5 7 2 3 8
2) 7 8 3 5 2
3) 2 3 5 7 8
Операции:
· вставка
· удаление (3 варианта)
a. удаление листа – удаляет узел, обнуляем указатель родителя.
b. если один потомок
c. если два потомка:
выбираем самый большой из левого поддерева (самый правый из левого поддерева) или самый маленький из правого поддерева (самый левый из правого)
заменяем значение в х
удаляем лист
· поиск
Виды обходов дерева:
Обход двоичного дерева – это процесс, при котором каждый узел посещается только один раз.
1) симметричный обход - сначала в симметричный обход левого поддерева, затем посещения корня и потом в симметричный обход правого поддерева.
|
|
|
При симметричном обходе каждого из двоичных деревьев поиска, показанных на рис. 2, узлы посещаются в возрастающем порядке: 2, 3, 5, 7, 8.
2) прямой обход - Для корня дерева рекурсивно вызывается следующая процедура:
Посетить узел
Обойти левое поддерево
Обойти правое поддерево
3) Обратный обход
Обойти левое поддерево
Обойти правое поддерево
Посетить узел
Балансировка деревьев
AVL деревья
Деревья бывают сбалансированные и несбалансированные (они получаются из частично или полностью отсортированных списков)
У сбалансированного дерева каждый узел удовлетворяет условию: для любого узла разность длин левого и правого поддерева не больше 1.
AVL дерево: balance {-1,0,1} = высота правого поддерева - высота левого поддерева
Обычная вставка может разбалансировать дерево.
Способы балансировки дерева:
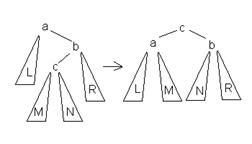
1) левое вращение
2) правое вращение
3) двойное левое вращение (простое правое + простое левое)
4) двойное правое вращение (простое левое + простое правое)
левое вращение правое вращение


двойное левое вращение (простое правое + простое левое)
двойное правое вращение (простое левое + простое правое)

Параграф 9
стандартная библиотека шаблонов STL (Standard Template Library) (стр 522)
Библиотека STL – набор шаблонных классов и функций общего назначения.
Основную роль в разработке STL сыграли Степанов и Страуструп
Ядро библиотеки состоит из трех ключевых элементов:
1) шаблоны классов-контейнеров (контейнеры)
2) итераторы
3) обобщенные алгоритмы (алгоритмы)
Контейнеры (стр 522)– объекты содержащие другие объекты, существует несколько типов контейнеров, например:
1) Последовательные контейнеры(базовые в STL): vector – определяет динамический массив, queue – двустороннюю очередь, а класс list – обеспечивает работу с линейным списком
2) Ассоциативные контейнеры(деревья): класс map позволяющий хранить пару «ключ-значение», multimap – ключ – несколько значений //переводчик
Каждый контейнерный класс определяет набор функций, который можно применять к данному контейнеру.
Итераторы (стр 522) – объекты действующие подобно указателям, позволяют циклически опрашивать содержимое контейнера. Существует пять типов итераторов:
|
|
|
1) произвольного доступа – random acces – сохраняют и считывают значения, позволяют организовать произвольный доступ к элементам
2) двунаправленные – bidirectional - сохраняют и считывают значения, обеспечивают инкрементно – декрементное перемещение
3) однонаправленные – forward - сохраняют и считывают значения, обеспечивают только инкрементное перемещение
4) входные – input – считывают, но не записывают значения, обеспечивают инкрементное перемещение
5) выходные – output – записывают, но не считывают значения, обеспечивают инкрементное перемещение
Алгоритмы (стр 551) - обрабатывают данные, содержащиеся в контейнерах. Позволяют работать с двумя различными типами контейнеров одновременно (последовательные и ассоциативные). Требуется заголовок - <algorithm>
|
|
|


