 |
III.Рабочие формулы и единицы измерения.
|
|
|
|
Дата Фамилия Тимофеев Группа
Лабораторная работа №65
I.Название работы:
Интерференция света. Кольца Ньютона
Цель работы
Получить на экране кольца Ньютона, используя красный и зеленый светофильтры, измерить радиусы нескольких колец, расстояния d1 и d2, рассчитать радиус кривизны линзы
II.Краткое теоретическое обоснование:
Интерференция света называют явления, возникающие при наложении когерентных световых волн, в результате чего происходит перераспределение светового потока в пространстве, и в одних местах возникают максимумы, а в других – минимумы интенсивности света.
Волны называются когерентными, если они имеют одинаковую частоту, направление и разность фаз возбуждаемых волнами колебаний остается постоянной во времени.
Естественные источники света являются некогерентными вследствие несвязанности волн, испускаемых атомами светящегося тела.
Когерентные световые волны можно получить, разделив (с помощью отражений и преломлений) волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить друг на друга, наблюдается интерференция. Оптическая длина пути L равна произведению геометрической длины пути S на показатель преломления среды n.
L = nS (1)
Показатель преломления среды n называется отношение скорости света в вакууме c к скорости света в данной среде v
n = c / v (2)
Показанием преломления среды больше или равен единице. Существуют различные практические методы получения когерентных световых волн: метод Юнга, бипризма, Френеля и т.д.
Рассмотрим теоретическую схему интерференции. (Рис.1)
Рис.1
В точке O происходит разделение на две когерентные волны. До точки P первая волна проходит в среде с показателем преломления n1 путь S1, вторая волна проходит в среде с показателем преломления n2 путь S2. Пусть в точке O фаза колебания равна ωt, где ω – круговая частота колебания, t – время. Тогда первая волна возбудит в точке P колебание A1cos ω(t – S1 / v1) а вторая волна – колебание A2cos ω(t – S2 / v2). Здесь v1 = c/n1 и v2 = c/n2 – фазовые скорости волн. Поэтому, разность фаз колебаний возбуждаемых в точке P, будет равна
|
|
|
δ = ω 
= 
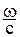(n2S2 – n1S1) (3)
Так как ω/с = 2πν/с = 2π/λ0, где λ0 – длина волны в вакууме, то (3) примет вид
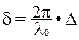(4)
где Δ = n2S2 – n1S1 называется оптической разностью хода складываемых волн.
Из формулы (4) следует, что если оптическая разность хода равна четному числу длин полуволн в вакууме,
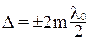(m = 0,1,2…) (5)
то разность фаз δ оказывается кратной 2π и колебания, возбуждаемые в точке P обеими волнами, будут происходить с одинаковой фазой, поэтому формула (5) есть условие интерференционного максимума.
Если оптическая разность хода равна нечетному числу длин полуволн в вакууме
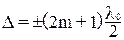(6)
то δ= ± (2m + 1)π и колебания в точке P находятся в противофазе. Поэтому формула (6) есть условие интерференционного минимума.
Формулы (5) и (6) применяют для конкретных задач интерференции.
Рассмотрим классический пример интерференции в тонком воздушном слое, известный под именем колец Ньютона.
Кольца Ньютона наблюдается при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки 1 и плоской выпуклой сферической линзы 2 с большим радиусом кривизны (рис. 2).
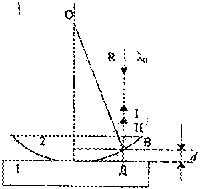Рис.2
Роль тонкой пленки, от поверхностей которой отражаются когерентные волны I и II, играет воздушный зазор переменной высоты d между пластинкой и линзой. При нормальном падении света получается следующая картина
Рис.3
в точке соприкосновения наблюдается черное пятно, окруженное рядом светлых и черных концентрических колец убывающей ширины. Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. В этом случае оптическая разность хода лучей I и II равна
|
|
|
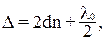(7)
где n – показатель преломления вещества прослойки (зазора), для воздуха n = 1.
Второе слагаемое в формуле (7) учитывает различия в условиях отражения от верхней и нижней поверхностей прослойки. Луч II при отражении от более плотной среды пластинки в точке Д изменяет фазу на π, то есть удлиняет свой путь на λ / 2.
Из рис.2
R2 = (R – d)2 + r2 = R2 – 2Rd + r2 (8)
Где R – радиус кривизны линзы, r – радиус окружности, всем точкам которой соответствует одинаковый зазор d. Ввиду малости d пренебрегаем величиной d2 по сравнению с 2Rd. Тогда
d = r2 / 2R (9)
Подставив (9) в (7), получим
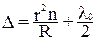(10)
Теперь воспользуемся полученными ранее условиями максимума (5) и минимума (6) при интерференции.
В результате для радиусов темных колец получим формулу
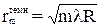(11)
где m = 0,1,2,…; λ = λ0n
Радиусы светлых колец находятся по формуле
(12)
Чем больше m, тем меньше различие между радиусами соседних колец, то есть тем ближе друг к другу кольца.
Кольца Ньютона наблюдаются и в проходящем свете.
Правильная форма колец Ньютона легко искажается при незначительных погрешностях выпуклой поверхности линзы и верхней пластинки.
Наблюдение формы колец Ньютона позволяет осуществить быстрый и точный контроль качества шлифовки плоских пластин и линз, а также близость поверхностей линз к сферической форме.
Измеряя радиусы колец rm, определяют R при заданной λ0 и, наоборот, вычисляют длину волны λ0 падающего света при заданном R линзы.
Если падающий свет – немонохроматический, то разным λ соответствует разные rm, то есть вместо черных и светлых колец получим систему цветных колец.
Полая в (11) m = 1, найдем область, занимающую кольцами первого порядка, m = 2 – кольцами второго порядка и т.д. Из (11) видно, что фиолетовый (400 нм) максимум второго порядка совпадает с темно – красным (800 нм) максимом первого порядка. Возможны и другие совпадения. Так как, кроме того, каждое кольцо имеет заметную ширину и в нем осуществляется плавный переход от максимума к минимуму, то даже в пределах первого порядка происходит значительное наложение одних цветов на другие; в еще большей степени это имеет место у высших порядков. В результате такого наложения возникает своеобразное чередование оттенков, совершенно не напоминающие последовательности «радужных цветов».
|
|
|
III.Рабочие формулы и единицы измерения.
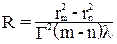
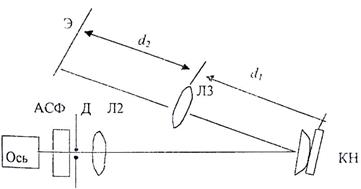
IV.Схема установки.
|
|
|
