Главная | Обратная связь | Поможем написать вашу работу!

Процентные точки распределения серий

ВВЕДЕНИЕ

На практике при анализе случайных данных часто возникает ситуации, когда необходимо установить, являются ли полученные оценки параметров статистически независимыми или же они подвержены тренду. Так как имеющиеся данные могут иметь различные функции распределения, то целесообразно принимать решение о наличии тренда на основе использования свободных от распределений или непараметрических методов, в которых относительно функции распределения полученных данных не делается никаких предположений. Или же данных настолько мало, что корректно проверить гипотезу о наличии конкретного распределения невозможно. Наиболее известными не зависящих от формы распределения методами, которые применяются для оценки наличия тренда в совокупности данных, являются: критерий серий и критерий инверсий.

1. КРИТЕРИЙ СЕРИЙ

Рассмотрим последовательность N значений случайной величины x(k) и каждое значение отнесем к одной из двух взаимно исключающих категорий, которые обозначим знаками плюс (+) и минус (-). В качестве примера рассмотрим последовательность измеренных значений величины x_i при i = 1, 2, 3,..., N, среднее значение которых равно . Каждое наблюденное значение
x_i³ обозначим (+), а если x_i< , то (-).

Полученная последовательность наблюдений, имеющих знак плюс или минус, может выглядеть следующим образом:

+ + - + + - + + + - + - - + - - + - - -

1 2 3 4 5 6 7 8 9 10 11 12

Серией называется последовательность одинаковых значений, перед которыми или после которых расположены значения другой категории или наблюдения отсутствуют вообще.

В рассмотренном примере имеется r = 12 серий в последовательности из N = 20 наблюдений.

Число серий, которое встречается в последовательности наблюдений, позволяет определить, являются ли результаты независимыми случайными наблюдениями над одной и той же случайной величиной. Если после-довательность N наблюдений представляет собой независимые наблюденные значения одной и той же случайной величины, т. е. вероятность знаков (+) и (-) не меняется от одного наблюдения к другому, то выборочное распределение числа серий в последовательности есть случайная величина r(k) со средним значением

(1)

и дисперсией

(2)

где N₁- число наблюдений со знаком (+), N₂- число наблюдений со знаком (-). В частном случае, когда N₁ = N₂ =N/2, соотношения (1) и (2) перепишутся в виде

(3)

(4)

В приложении 1 приведена таблица, содержащая данные о 100a-про-центных точках функции распределения r(k).

Если последовательность значений содержит тренд, то это означает, что вероятность знаков (+) или (-) меняется от одного наблюденного значения к другому. Наличие тренда можно проверить следующим образом. Рассмотрим гипотезу об отсутствии тренда, т. е. предположим, что полученные данные представляет собой независимые значения одной и той же случайной величины. Полагая, что число наблюденных значений со знаком (+) равно числу значений со знаком (-), можно считать, что число серий в последовательности будет иметь выборочное распределение, представленное в приложении 1. Гипотезу можно подвергнуть проверке при любом уровне значимости a путем сопоставления фактического числа серий с граничными значениями r_{n; 1-}_a_/2 и r_n;_a_/2, где n=N/2. Если фактическое число серий выходит за границы этого интервала, гипотезу следует отвергнуть при выбранном уровне значимости. В противном случае ее можно принять.

Например, имеется последовательность из N=20 чисел: 5,5; 5,1; 5,7; 5,2; 4,8; 5,7; 5,0; 6,5; 5,4; 5,8; 6,8; 6,6; 4,9; 5,4; 5,9; 5,4; 6,8; 5,8; 6,9; 5,5.

Определим, являются ли независимыми наблюденные значения, путем проверки числа серий, которые встречаются, если отсчитывать наблюденные значения от их медианы. Выполним проверку при уровне значимости a = 0,05.

Просматривая выборку, можно убедиться, что медианой данного ряда является значение x = 5,6. Примем, что числа более 5,6 имеют знак (+), а менее 5,6 - знак (-). В результате получаем последовательность

- - + - - + - + - + + + - - + - + + + -

1 2 3 4 5 6 7 8 9 10 11 12 13

Таким образом, имеется 13 серий, представляющих последовательность 20 наблюденных значений.

Рассмотрим гипотезу о независимости наблюденных значений. Область принятия этой гипотезы определяется интервалом [r_{10; 1-}_a/2 < r £ r_10;_a/2].
По данным приложения 1 при a = 0,05 находим r_{10; 1-}_a/2 = r_{10; 0,975} = 6 и
r_10;_a/2 = r_{10; 0,025} = 15. Нулевая гипотеза принимается, так как значение r = 13 входит в интервал между 6 и 15. Другими словами нет причин подвергнуть сомнению то обстоятельство, что наблюденные значения независимы. Это значит, что нет никаких доказательств присутствия тренда.

2. КРИТЕРИЙ ИНВЕРСИЙ

Рассмотрим последовательность N значений случайной величины x(k). Обозначим эти значения символом x_i, где i == 1, 2, 3,..., N.

Подсчитаем теперь число случаев, когда x_i> x_j, при i < j. Каждое такое неравенство называется инверсией. Общее число инверсий обозначается символом А, которое формально определяется так.

По ряду значений x₁, x₂…, x_N определим величину

Тогда где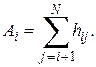

Например,

и т.д.

Для примера рассмотрим последовательность N = 8 значений: x₁=5, x₂=3, x₃=8, x₄=9, x₅=4, x₆=1, x₇=7, x₈=5. В этой последовательности x₁ > x₂, x₁ > x₅и
x₁ > x₆, откуда находим А₁ = 3 инверсиям для x₁. Сопоставляя значение x₂с последующими значениями ряда (т. е. при i = 2 и i < j = 3, 4,..., 8), можно найти, что x₂ > x₆и только. Поэтому число инверсий для x₂ составляет A₂ = 1. Продолжая анализ, можно видеть, что A₃ = 4, A₄ = 4, A₅ = 1, A₆ = 0, A₇ = 1. Общее число инверсий составит A = A₁ + A₂ + … + A₇ = 3+1+4+4+1+0+1 = 14.

Если последовательность N наблюдений содержит независимые значения одной и той же случайной величины, то число инверсий есть случайная величина А(k) со средним значением

(5)

и дисперсией

(6)

В приложении 2 содержатся данные о 100a-процентных точках функции распределения величины А(k).

Критерий инверсий вообще говоря, имеет большую мощность, чем критерий серий, при выявлении монотонного тренда в последовательности наблюдений. Однако критерий инверсий обладает малой мощностью при выявлении колебательного тренда.

Например, проверим последовательность N = 20 значений, рассмотренных ранее, на наличие тренда при уровне значимости a = 0,05. Число инверсий в этом случае таково:

А₁

А₂

А₃

А₄

А₅

А₆

А₇

А₈

А₉

А₁₀

А₁₁

А₁₂

А₁₃

А₁₄

А₁₅

А₁₆

А₁₇

А₁₈

А₁₉

Общее число инверсий А = 62.

Рассмотрим гипотезу о том, что наблюдения представляют независимые значения случайной величины х(k), не содержащей тренда. Область принятия гипотезы определяется неравенством A_{20; 1-}_a_/2 < A £ A_20;_a_/2. По данным приложения 2 при a = 0,05 находим A_20;1-_a_/2=A_20;0,975= 64 и A_20;_a_/2=A_20;0,025= 125.

Следовательно, гипотезу отвергают при 5%-ном уровне значимости, так как значение А = 62 не попадает в интервал между 64 и 125.

Заметим, что гипотеза о независимости этой же последовательности значений при использовании критерия серий была принята. Этот факт иллюстрирует разницу в чувствительности двух методов проверки.

3. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

В соответствии с вариантом проверить гипотезу о наличии тренда, используя критерии серий и инверсий при уровнях значимости a = 5% и a=1%.

№ варианта	Значения ряда
	7,5; 7,1; 7,7; 7,2; 4,8; 7,7; 7,0; 6,5; 7,4; 7,8; 6,8; 6,6; 4,9; 7,4; 7,9; 7,4; 6,8; 7,8; 6,9; 7,5
	9,5; 9,1; 9,7; 9,2; 4,8; 9,9; 9,0; 6,5; 9,4; 9,8; 6,8; 6,6; 4,9; 9,4; 9,9; 9,4; 6,8; 9,8; 6,9; 9,5
	33,5; 33,1; 33,7; 33,2; 14,8; 33,1; 33,0; 16,5; 33,4; 33,8; 16,8; 16,6; 14,11; 33,4; 33,9; 33,4; 16,8; 33,8; 16,9; 33,5
	54,5; 54,1; 54,7; 54,2; 64,8; 54,1; 54,0; 66,5; 54,4; 54,8; 66,8; 66,6; 64,1; 54,4; 54,9; 54,4; 66,8; 54,8; 66,9; 54,5
	77,5; 77,1; 77,7; 77,2; 84,8; 77,1; 77,0; 86,5; 77,4; 77,8; 86,8; 86,6; 84,1; 77,4; 77,9; 77,4; 86,8; 77,8; 86,9; 77,5
	33,5; 33,1; 33,7; 33,2; 31,8; 33,1; 33,0; 36,5; 33,4; 33,8; 32,8; 36,6; 38,1; 33,4; 33,9; 33,4; 36,8; 33,8; 36,9; 33,5; 33,5; 33,1; 33,7; 33,2; 38,8; 33,11; 33,0
	33,5; 33,1; 33,7; 33,2; 44,8; 33,1; 33,0; 46,5; 33,4; 33,8; 46,8; 46,6; 44,1; 33,4; 33,9; 33,4; 46,8; 33,8; 46,9; 33,5; 33,9; 33,4; 46,8; 33,8; 46,9; 33,5
	33,5; 33,1; 33,7; 33,2; 37,8; 33,1; 35,0; 36,5; 35,4; 33,8; 36,8; 36,6; 34,1; 33,4; 33,9; 33,4; 35,8; 33,8; 36,9; 33,5
	92; 95; 96; 89; 86; 90; 88; 89; 86; 90; 83; 85; 80; 78; 89; 86; 90; 83; 85; 76; 72; 75
	13; 16; 15; 20; 15; 16; 15; 20; 19; 21; 26; 24; 30; 32; 30; 20; 19; 21; 26; 24; 35; 34; 40; 39;
	55; 60; 50; 30; 75; 70; 60; 55; 40; 45; 55; 60; 50; 43; 55; 60; 50; 70; 60; 55; 40; 45
	209,2; 209,5; 210,2; 212,0; 214,3; 221,8; 214,6; 214,4; 208,5; 208,7; 206,2; 207,8; 215,3; 216,7; 212,3; 212,0; 204,2; 210,2; 210,5; 205,9; 215,7; 213,8; 215,2; 202,7
	204,0; 203,3; 198,2; 199,9; 212,5; 210,2; 211,3; 210,4; 209,6; 203,7; 213,2; 209,6; 208,4; 214,9; 212,8; 214,8; 208,1; 207,9; 211,0; 206,2; 212,3; 216,2; 208,4; 210,8
	205,2; 204,8; 198,7; 205,8; 208,1; 211,9; 212,9; 209,0; 199,0; 197,7; 202,0; 213,1; 207,5; 209,9; 210,6; 212,3; 197,2; 210,6; 199,5; 215,3; 206,9; 207,1; 213,6; 212,2
	199,1; 207,2; 200,8; 201,2; 209,6; 209,5; 206,8; 214,2; 204,6; 207,0; 200,8; 204,6; 212,2; 209,8; 207,6; 212,6; 214,7; 207,5; 205,8; 200,9; 211,4; 211,2; 214,4; 212,6
	204,1; 196,6; 204,6; 199,4; 209,6; 209,2; 206,1; 207,1; 200,2; 205,5; 208,0; 202,7; 203,5; 206,9; 210,6; 212,3; 201,1; 209,2; 205,5; 200,0; 209,1; 206,3; 209,8; 211,4
	201,3; 203,1; 196,3; 205,5; 208,0; 207,9; 205,3; 203,6; 202,2; 204,4; 202,1; 206,6; 210,0; 209,4; 209,1; 207,0; 194,1; 211,0; 208,4; 202,6; 215,6; 211,8; 205,1; 209,0
	204,8; 201,3; 208,4; 212,3; 214,5; 207,5; 212,9; 204,3; 200,6; 202,3; 204,3; 201,4; 209,1; 205,8; 212,0; 204,2
	209,5; 206,8; 214,2; 204,6; 207,0; 200,8; 204,6; 212,2; 209,8; 207,6; 212,6; 214,7; 207,5; 205,8; 200,9; 211,4; 211,2; 214,4; 212,6
	196,3; 205,5; 208,0; 207,9; 205,3; 203,6; 202,2; 204,4; 202,1; 206,6; 210,0; 209,4; 209,1; 207,0; 194,1; 205,3; 203,6; 202,2; 204,4; 202,1

Приложение 1

Процентные точки распределения серий

n=N/2	Уровень значимости, a
0,99	0,975	0,95	0,05	0,025	0,01

Приложение 2

Воспользуйтесь поиском по сайту: