 |
Регулирование скорости, момента, тока ДПТ НВ изменением сопротивления в якорной цепи.
|
|
|
|
Ответ: Из уравнения электромеханической характеристики двигателя постоянного тока независимого возбуждения следует, что возможны три способа регулирования его угловой скорости:
1) регулирование за счет изменения величины сопротивления реостата в цепи якоря,
2) регулирование за счет изменения потока возбуждения двигателя Ф,
3) регулирование за счет изменения подводимого к обмотке якоря двигателя напряжения U. Ток в цепи якоря Iя и момент М, развиваемый двигателем, зависят только от величины нагрузки на его валу.
Рассмотрим первый способ регулирования скорости двигателя постоянного тока изменением сопротивления в цепи якоря. Схема включения двигателя для этого случая представлена на рис. 1, а электромеханические и механические характеристики — на рис. 2, а.

Рис. 1. Схема включения двигателя постоянного тока независимого возбуждения
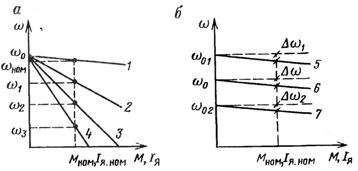
Рис. 2. Механические характеристики двигателя постоянного тока при различных сопротивлениях цепи якоря (а) и напряжениях (б)
Изменяя сопротивление реостата в цепи якоря можно получить при номинальной нагрузке различные угловые скорости электродвигателя на искусственных характеристиках — ω1, ω2, ω3.
Проведем анализ данного способа регулирования угловой скорости двигателей постоянного тока с помощью основных технико-экономических показателей. Так как при данном способе регулирования изменяется жесткость характеристик в широких пределах, то при скоростях менее половины номинальной стабильность работы двигателя резко ухудшается. По этой причине диапазон регулирования скорости ограничен (D= 2- З).
Скорость при данном способе можно регулировать в сторону уменьшения от основной, о чем свидетельствуют электромеханические и механические характеристики. Высокую плавность регулирования трудно обеспечить, так как потребовалось бы значительное количество ступеней регулирования и соответственно большое число контакторов. Полное использование двигателя по току (нагреву) в этом случае достигается при регулировании с постоянным моментом нагрузки.
|
|
|
Недостатком рассматриваемого способа является наличие значительных потерь мощности при регулировании, которые пропорциональны относительному изменению угловой скорости. Достоинством рассмотренного способа регулирования угловой скорости являются простота и надежность схемы управления.
Учитывая большие потери в реостате при малых скоростях, данный способ регулирования скорости применяется для приводов с кратковременным и повторно-кратковременным режимами работы.
Примем U = U н=const,Φ=Φн=const, а сопротивление якорной цепи представим соотношением
R яц= R я+ R д.
Подставим R яц в уравнение механической характеристики (2.7) вместо R я и получим
ω= U н/(K Φн)−(R я+ R д)· M /(K Φн)2.
Запишем полученное уравнение механической характеристики в относительных единицах
(2.29)
ν=1−(1+ r)μ,
где r = R д/ R я – относительное значение добавочного сопротивления в цепи якоря.
Если принять μ=const, то уравнение (2.29) является характеристикой регулирования скорости. Можно отметить, что это характеристика линейна и имеет вид (рис. 2.6.а).
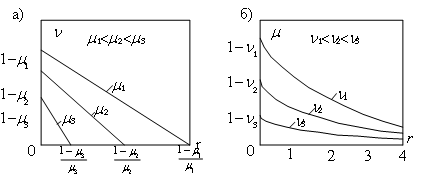
Рис. 2.6. Регулировочные характеристики при изменении сопротивления в цепи якоря
Диапазон изменения скорости ν∈[0,(1−μ)]. При этом регулирующий параметр должен изменяться в диапазоне r ∈[(1−μ)/μ,0]. Передаточный коэффициент регулирования
(2.30)
k ν=Δν/Δ r =−μ.
Теперь примем ν=const и перепишем уравнение (2.29) в виде
(2.31)
μ=(1−ν)/(1+ r).
Уравнение (2.31) является характеристикой регулирования момента. Можно отметить, что она нелинейна и имеет вид рис. 2.6.б. При увеличении сопротивления в цепи якоря момент уменьшается, асимптотически приближаясь к нулю. Диапазон изменения момента μ∈[0,(1−ν)] при изменении регулирующей координаты в диапазоне r ∈[∞,0]. Передаточный коэффициент регулирования можно получить только для линеаризованной характеристики. Для малых отклонений координат имеем
|
|
|
(2.32)
k μ=Δμ/Δ r = d μ/ drr = r 0=−(1−ν)/(1+ r 0)2,
где r 0 – исходное значение регулирующего параметра, относительно которого рассматриваются малые отклонения.
Учитывая, что в данном случае ηэ=ν, уравнение (2.29) может быть использовано для определения электромагнитного к.п.д. двигателя в процессе регулирования.
|
|
|


