Геометрия в старших классах: инструмент дьявола

Пол Локхард

Плач математика. Эссе о преподавании математики в школе

 

 

 

Аннотация

 

Эссе о преподавании математики в средней школе. Хотя в сочинении говорится об американской современной средней школе, многие проблемы, идентифицируемые Локхардом, относятся к любой стране мира, за исключением, возможно, Эльдорадо, которой нет. Еще менее привязаны к американской реальности размышления автора о том, что такое математика и как она должна преподаваться.

Даже если вы не математик и не имеете отношения к преподаванию, вы найдете это эссе интересным, а возможно, и сделаете для себя несколько небольших открытий и сломаете кое-какие стереотипы. В конце концов, вы ведь учили математику в школе!

 

Пол Локхард

ПЛАЧ МАТЕМАТИКА

 

От переводчика

 

Представляю вам свой перевод эссе Пола Локхарда «Плач математика» (Paul Lockhart. A Mathematician's Lament) о преподавании математики в средней школе. Хотя в сочинении говорится об американской современной средней школе, многие проблемы, идентифицируемые Локхардом, относятся, по моему мнению, к любой стране мира, за исключением, возможно, Эльдорадо, которой нет. Еще менее привязаны к американской реальности размышления автора о том, что такое математика и как она должна преподаваться.

Даже если вы не математик и не имеете отношения к преподаванию, думаю, вы найдете это эссе интересным, а возможно, и сделаете для себя несколько небольших открытий и сломаете кое-какие стереотипы. В конце концов, вы ведь учили математику в школе!

Все комментарии в сносках мои. Их следует разделить на два типа: первые — именные, где я обязательно привожу английское и/или оригинальное написание имени, чтобы вам было легче найти библиографическую информацию; вторые — кратко разъясняющие некоторые реалии американской жизни, без понимания которых определенный смысл текста будет утерян.

Перевод всего эссе не завершен; здесь примерно половина текста, откомментированная, но, к сожалению, не вычитанная корректором, и потому корявая и полная опечаток. Прошу вашего прощения за «сырое» издание; мною движет желание поскорее поделиться этим замечательным сочинением. Будет и полный текст в виде одного файла, уже откорректированный, но на это потребуется некоторое время.

L. Fregimus Vacerro (http://fregimus.livejournal.com/)

 

Предисловие Кита Девлина

 

Эссе «Плач математика» написано Полом Локхартом, учителем математики в школе Св. Анны в Бруклине (шт. Нью-Йорк), в 2002 г. С тех пор оно стало известно в кругах математиков и преподавателей математики, но он так и не опубликовал его. Случайно обнаружив это сочинение несколько месяцев тому назад, я сразу решил, что оно заслуживает более широкой аудитории. Я связался с Полом, и он позволил мне опубликовать этот «плач» в «Эм-Эй-Эй Онлайн[1]». Положа руку на сердце, это лучшая критика школьного математического образования, какую я только встречал.

Пол — ученый-математик, посвятивший свою карьеру преподаванию математики в школе. Он заинтересовался математикой в возрасте 14 лет (и не в школе, как он попросил уточнить) и читал запоем, в основном заинтересовавшись аналитической теорией чисел. Бросив учебу на первом курсе, он посвятил себя математике, зарабатывая на жизнь программированием и преподаванием в начальной школе. Затем он начал работать с Эрнстом Штраусом[2]в университете Калифорнии в Лос-Анджелесе. Штраус познакомил его с Эрдёшем[3], который устроил Локхарта в аспирантуру. Локхарт защитил диссертацию в университете Коламбия в 1990 г., и был сотрудником Института математических исследований (MSRI) в Беркли и профессором в университете Брауна (шт. Род-Айленд) и в университете Калифорнии в Санта-Круз. Его научные интересы включают автоморфные функции и диофантову геометрию.

После нескольких лет преподавания математики в университете Пол решил вернуться в школу и учить детей. В 2000 г. он нашел работу в школе св. Анны, где, по его словам, «счастлив преподавать настоящую математику самым подрывным образом».

Он преподает математику во всех классах, от подготовительного до 12-го, и особенно заинтересован прививать математический взгляд самым маленьким ученикам. «Я хочу дать им понять, что их ум — это игровая площадка, и математика случается именно там. Я наблюдаю огромный энтузиазм и у детей, и у родителей, и гораздо меньший у администраторов средней руки», — писал он мне. Где-то я такое уже слышал…

Кит Девлин [4], март 2008 г.

 

Вступление

 

Музыкант просыпается от кошмарного сна. Во сне он видел, будто музыкальное образование стало обязательным. «Мы помогаем ученикам вступить в этот заполненный звуками мир», — преподаватели, школьная система и государство принялись за этот жизненно важный проект. Проводятся исследования, образуются комиссии, принимаются решения… И все это без единого совета музыканта или композитора!

Музыканты, как известно, записывают свои идеи нотами; выходит, эти черные кружочки и палочки и есть «язык музыки». Важно, чтобы ученики свободно говорили на этом языке, если они собираются выучиться музыке; само собой, было бы абсурдно ожидать от ребенка, что он сможет спеть песенку или сыграть мелодию на каком-нибудь инструменте, если он не выучил музыкальной нотации и теории. А играть и слушать музыку, не говоря уж о сочинении собственной пьесы, учат в вузе и в аспирантуре.

А цель обучения младших и средник классов — научить школьников языку музыки: надо ведь заучить все правила обращения с этими символами! «На уроке музыки мы берем нотную бумагу, учительница пишет на доске ноты, а мы переписываем их или транспонируем в другую тональность. Нам надо научиться рисовать скрипичный и басовый ключи, и не путаться с тональностями. Наша учительница очень строгая. Она всегда смотрит, чтобы четвертные ноты были полностью закрашены. Однажды я решала хроматическую шкалу, и все сделала верно, но мне поставили двойку, потому что я нарисовала штили не в ту сторону».

Даже самые маленькие могут этому научиться! Третьекласснику стыдно не знать квинтового круга. «Мне пришлось нанимать сыну репетитора. Он просто не может делать домашнюю работу по музыке. Канючит, что ему скучно. Смотрит в окно, что-то насвистывает и напевает дурацкие песенки».

В старших классах программа напряженная: ученики готовятся к ЕГЭ и вступительным экзаменам. Они изучают гаммы и лады, разные размеры, учат гармонию и контрапункт. «Им надо многому научиться, но на младших курсах, когда они услышат все это, они поймут, как важно было пройти школьную программу». Конечно, не все студенты собираются специализироваться на музыке, так что немногие из них вообще когда-либо услышат звуки, которые обозначают черные кружочки нот. Тем не менее, чрезвычайно важно, чтобы каждый член общества мог распознать модуляцию или фугу, даже те, кто никогда их не слышал. «По правде говоря, большинство учеников успевают по музыке довольно средне. Они только и дожидаются звонка с урока, ничего не умеют, домашнее задание пишут, как курица лапой. Они не думают о том, насколько важна музыка в современном мире, они хотят только окончить школу, пройти самый минимум и получить оценку в аттестат. Наверное, есть просто способные и неспособные к музыке. У меня была одна замечательная ученица. Ее нотные листы были безупречны — каждая нотка на своем месте, каллиграфический почерк, и диезы, и бемоли красиво написаны. Когда-нибудь она станет великим композитором!»

Наш музыкант просыпается в липком холодном поту и понимает, что это был, к счастью, просто сон. «Конечно же! — говорит он вслух сам себе, чтобы успокоиться, — Ни одно общество не дойдет до такого, чтобы свести прекрасное и осмысленное искусство музыки к такой бездумной и тривиальной формальности; ни одна культура не может быть так жестока к детям, чтобы лишить их такого естественного и приятного способа самовыражения. Какая чушь мне снится!»

Тем временем, на другом конце города от похожего кошмара просыпается художник…

* * *

Я оказался в обычном классе — никаких мольбертов, никаких красок. «Мы не берем в руки красок до десятого класса, — сказали мне ученики, — В седьмом классе мы учим только теорию красок и кистей». Мне показали тетрадь по рисованию: в ней были закрашенные квадраты разных цветов с пустыми местами рядом с ними. Задание требовало вписать названия цветов рядом с квадратами. «Мне нравится рисование! — сказал кто-то из них, — Мне говорят, что делать, и я так и делаю. Это просто!»

После занятий я говорил с учителем. «Выходит, ученики ничего не рисуют?» — спросил я. «В старших классах они будут раскрашивать книжки-раскраски[5]

— А эти… э-э-э… старшие классы…

— Ах, с углубленным изучением? В последнее время, все больше детей пытаются в них попасть. Я думаю, это родители их подталкивают, ведь запись об этом классе в аттестате дает преимущества при поступлении в вуз[6].

— Преимущества? А зачем нужно вузу, чтобы студенты умели закрашивать книжки-раскраски указанным цветом?

— А как же! Этим они демонстрируют ясность логического мышления! И, разумеется, если школьник планирует поступать на какой-нибудь дизайнерский факультет, лучше всего получить эти знания еще в школе.

— Понятно… А когда ученики начинают рисовать… ну, так, на чистом холсте?

— Вы говорите, как один из моих старых профессоров! Они все время говорят о самовыражении в искусстве, о чувствах и всякой абстрактной дребедени. Я сама, между прочим, окончила художественный факультет, но мне ни разу не приходилось рисовать целую картину на чистом холсте. А в классе мы используем комплекты раскрасок, что закупает школа.

* * *

Увы, наша система преподавания школьной математики — именно такой кошмар. На самом деле, если бы мне велели придумать систему для уничтожения врожденного детского любопытства, стремления к поиску системы, я бы не смог сделать эту работу лучше, чем она уже делается: у меня попросту не хватило бы воображения дойти до этих бессмысленных и бездушных методик современного школьного математического образования.

Причем все понимают, что что-то не в порядке. Политики говорят: «Нам нужны более высокие стандарты». Школы говорят: «Нам нужно больше денег и оборудования». Каждый говорит свое, но все они неправы. Но тех единственных, кто понимает, что происходит, не только не слушают, но и чаще других обвиняют во всем происходящем. Я говорю о детях. Они говорят: «Уроки математики скучные и глупые». И они правы.

 

Математика и культура

 

Первое, что нам следует понять — то, что математика есть искусство. Различие между математикой и другими искусствами, такими, как музыка или рисование, состоит в том, что наша культура не признает ее искусством. Все понимают, что поэты и музыканты создают произведения искусства, выражая себя в слове, картине и звуке. Наше общество, можно сказать, щедро на признание искусством области творчества: архитекторы, шеф-повара и даже телеведущие признаются людьми искусства. Так почему же не математики?

Часть проблемы в том, что ни у кого в обществе нет даже приблизительного понятия о том, что же делают математики. Общее понимание, похоже, таково, будто математика как-то связана с естественными науками[7]: математики помогают ученым своими формулами, или вычисляют огромные числа на компьютерах для той или иной научной задачи. Без сомнения, если бы потребовалось поделить мир на «поэтических мечтателей» и «рациональных мыслителей», большинство людей определило бы математиков в последнюю категорию.

Тем не менее, нет ничего на свете столь же мечтательного и поэтичного, столь же радикального, взрывного и психоделичного, как математика. Она настолько же умопомрачительна, как физика или космология (в конце концов, математики мыслили о черных дырах задолго до того, как астрономы открыли их), и гораздо свободнее в выразительных средствах, чем поэзия, живопись или музыка (ибо они зависимы от свойств материальной Вселенной). Математика — чистейшее из искусств и самое непонятое из них.

Позвольте мне объяснить, что такое математика и чем занимаются математики. Я не найду лучшего описания, чем то, что дает Г. Г. Харди[8]:

 

Математик, как и художник и поэт, создает узоры. И если его узоры долговечнее, то это потому что они сотканы из идей.

 

Значит, математики сидят и ткут узоры из идей. Какие узоры? Из каких идей? Идеи о носорогах? Нет, оставим их биологам. Идеи о культуре и языке? Обычно нет. Эти вещи слишком сложны на вкус математика. Если мы должны найти объединяющий эстетический принцип математики, то он будет таков: простое — прекрасно. Математикам нравится думать о простых вещах, и самые простые вещи — воображаемые.

Например, когда я в настроении подумать о геометрических формах — а я часто бываю в таком настроении, — я могу представить себе треугольник, вписанный в прямоугольник:

 

 

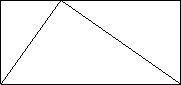
Я думаю о том, какую часть прямоугольника занимает треугольник. Примерно две трети, похоже? Тут важно понимать, что я думаю не о рисунке треугольника в прямоугольнике. И я говорю не о треугольнике-части фермы моста. В этом нет скрытой практической цели. Я играю. Это и есть математика: интерес, игра, развлечение собственным воображением. С одной стороны, вопрос о том, какую часть прямоугольника занимает треугольник, попросту не имеет смысла для реальных объектов! Даже самый тщательно изготовленный треугольник есть лишь безнадежно сложное сооружение из подрагивающих атомов, и его размер меняется каждую малую долю секунды — если мы не говорим о неких приближенных измерениях. Это не просто, и, следовательно, это некрасивый вопрос, зависящий от множества деталей реального мира. В этом проявляется эстетика математики. Мы оставим этот вопрос ученым. Математический вопрос задается о воображаемом треугольнике, вписанном в воображаемый прямоугольник. Его стороны совершенны, потому что я так хочу — или потому что мне нравится думать о таких объектах. Это лейтмотив математики: ее объекты таковы, каковыми вы их представите. Ваш выбор безграничен; реальность не встает на вашем пути.

С другой стороны, как только вы сделали выбор (например, я могу сделать мой треугольник симметричным или нет), ваши создания ведут себя определенным образом, хотите вы того или нет. Удивительнейшее свойство воображаемых узоров: они вам отвечают! Треугольник занимает определенную часть прямоугольника, и не в моих силах изменить эту часть. Это число, может быть, оно равно двум третьим, может быть, нет, но главное, что я не могу просто так решить, каким оно будет. Я должен его найти.

Так, мы начинаем играть, и строим воображаемые узоры, и задаем вопросы об этих узорах. Но как мы находим ответы на эти вопросы? Совсем не так, как в естественных науках. Нет такого эксперимента в лаборатории с пробирками или на какой-нибудь специальной технике, чтобы исследовать мой вымысел. Единственный способ узнать правду о воображаемых объектах — это напрячь воображение, и это непростая работа.

В случае с нашим треугольником в прямоугольнике, я вижу кое-что простое и красивое:

 

 

Если я разрежу прямоугольник на две части по пунктирной линии, сразу видно, что стороны треугольника рассекают каждую из частей ровно надвое. Значит, вне треугольника такая же часть прямоугольника, что и внутри, и, следовательно, площадь треугольника в точности равна половине площади прямоугольника!

Вот так выглядит и ощущается математика. Это маленькое описание — пример искусства математика: он задает простые и элегантные вопросы о воображаемых объектах, а затем придумывает правильные и красивые объяснения. Ничего подобного этому царству чистой идеи нет; это очаровательно, занимательно и не стоит ничего!

Понятно, но откуда взялась моя идея? Как я догадался провести линию? Как живописец знает, где приложить кисть? Вдохновение, опыт, пробы и ошибки и слепая удача. В этом и состоит искусство — создавать эти прекрасные поэмы мысли, эти сонеты чистого разума. В этом виде искусства есть что-то чудесно преобразующее нас. Отношение между треугольником и прямоугольником было загадкой, и одна маленькая линия сделала разгадку очевидной. Я не мог ее увидеть, и вдруг неожиданно увидел. Каким-то образом я создал глубокую и простую красоту из ничего, и изменил этим себя — разве не это мы называем искусством?

Вот почему мне так горько видеть, во что превращают математику в школе. Очаровательная, плодотворная игра воображения выхолащивается до стерильного набора зазубриваемых фактов и способов решения. Вместо простого и естественного вопроса о геометрических формах и творческого и полезного процесса изобретения и открытия ученикам дают вот это:

 

 

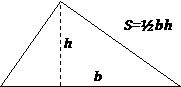
«Площадь треугольника равна половине произведения его основания на высоту». От учеников требуется запомнить формулу и «применять» ее раз за разом в «упражнениях». Уходит и радость, и дрожь нетерпения, и труд, и даже горечь творческого акта. Ведь это даже более не задача. Вопрос был задан вместе с ответом, и ученику ничего не осталось делать.

Мне следует здесь явно объяснить, против чего я возражаю. Я не против ни формул, ни запоминания интересных фактов. Это замечательно в контексте, и, как и заучивание слов при изучении языка, позволит вам создавать более глубокие произведения, полные тонких нюансов. Но сам по себе факт, что треугольник занимает половину описанного прямоугольника, не важен! Важна идея рассечь его прямой линией; важно то, как она вдохновляет на поиск других прекрасных идей и ведет к творческим прорывам при решении других задач — то, чего не дает вам простое утверждение факта.

Удаляя творческий процесс и оставляя лишь результат этого процесса, вы почти наверняка гарантируете, что никто не будет на самом деле заниматься предметом. Это все равно, что сказать, что Микеланджело создал чудесные скульптуры, при этом ни разу не показав их. Можно ли вдохновиться этим? (На самом деле, все гораздо хуже — по крайней мере, в последнем случае я бы знал, что эти произведения искусства существуют, но мне их попросту не показывают.)

Когда концентрируются на что, но игнорируют почему, от математики остается одна пустая оболочка, видимость. Искусство — не в истине, а в объяснении, аргументации. Объяснение дает истине контекст, определяет, о чем на самом деле говорится и что имеется в виду. Математика есть искусство объяснения. Если вы не дадите ученикам возможности заняться объяснением — формулировать свои собственные задачи, предлагать свои гипотезы, делать свои открытия, ошибаться, терпеть творческие неудачи, вдохновляться и складывать свои собственные, пусть и неуклюжие, объяснения и доказательства, — вы лишите их самой математики. Я не возражаю против формул и фактов. Я жалуюсь на отсутствие математики на наших уроках математики.

Если учитель рисования скажет вам, что живопись — это закрашивание пронумерованных областей на шаблоне, вы сразу почувствуете подвох. Сама культура скажет вам об этом — ведь существуют музеи и картинные галереи, и вы видите предметы искусства даже дома. Живопись хорошо понимается обществом как средство человеческого самовыражения. Подобно тому, если учитель астрономии скажет, что астрономия занимается предсказанием судьбы по дате рождения, вы сразу поймете, что он спятил, ведь наука до такой степени проникла в культуру, что почти каждый знает об атомах и галактиках и законах природы. Но если учитель математики даст вам понять, что математика занимается формулами, определениями и способами вычисления, которые надо запомнить, кто или что скажет вам правду?

Культурная проблема эта — чудовище, раскармливающее само себя: ученики узнают о математике от учителей, а учителя — от своих учителей, и непонимание и неприятие математики нашей культурой поддерживается бесконечно. Хуже того, бесконечная поддержка этой псевдоматематики с упором на точную, но неосмысленную манипуляцию с символами, создает свою культуру со своими ценностями. Адепты ее получают громадную самооценку от своих успехов. Меньше всего они хотят слышать о том, что математика в первую очередь — чистые творчество и эстетика. Многие выпускники университетов, которым десяток лет говорили, что у них талант к математике, с ужасом осознают, что к настоящей математике у них нет никакого таланта, и что на самом деле их талант следовать указаниям, и только. А математика — это не следование указателям, это расстановка указателей.

И ведь я даже еще не упоминал отсутствия математической критики в школе! Школьники так и не узнают ни о том, что математика, как и любая литература, создается людьми для забавы, игры ума, ни о том, что математические труды необходимо критиковать, ни того, что человек должен выработать математический вкус. Математический дискурс подобен поэме, и нам следует спрашивать, удовлетворяет ли он нашим эстетическим критериям: тверда ли его аргументация? есть ли в нем смысл? прост ли он и элегантен? позволяет ли он добраться до сути дела? Конечно же, в школе вы не найдете такой критики.

Почему мы не хотим, чтобы наши дети научились математике? Может быть, мы не доверяем им, или думаем, что это слишком сложно? Как будто мы чувствуем, что они могут прийти к собственному мнению о Наполеоне, но не о треугольниках. Я думаю, что причина в том, что мы, как культура, не знаем, что такое математика. Впечатление, которое мы получаем — будто это что-то такое холодное и сугубо техническое, чего, наверное, никто толком и не понимает: и ведь это выходит пророчество, исполняющее само себя, если такое вообще возможно.

Было бы полбеды, если бы наша культура была просто математически необразованной, а беда наша в том, что люди думают, будто они знают, что такое математика, и потому находятся под совершенно неверным впечатлением, будто математика чем-то практически полезна обществу. В этом уже видна огромная разница между восприятием математики и прочих искусств: математика рассматривается обществом, как некий инструмент решения естественнонаучных и технических задач. Каждый знает, что музыка и поэзия нужны для услады души и облагораживания духа (поэтому они едва присутствуют в школьной программе), но математика — о нет! — математика «важна».

 

Симплицио [9]. Ты утверждаешь, что математика не имеет практического приложения в обществе?

Сальвиати. Конечно же нет! Просто обращаю внимание, что из того, что некий предмет приводит к практическим последствиям, не следует, будто он предназначен для этого. Музыка ведет армии в бой, но люди сочиняют симфонии не для того. Микеланджело расписывал потолок, но в мыслях у него было кое-что и повыше.

Симплицио. Ведь нужно учить людей этим практическим результатам. Разве не нужны нам счетоводы, плотники и так далее?

Сальвиати. Много ли людей пользуются этой самой «практической» математикой, что они изучили в школе? Ты думаешь, будто плотникам нужна тригонометрия? Много ли ты знаешь взрослых, что умеют делить дроби или решать квадратные уравнения? Очевидно, что нынешнее практическое обучение не работает, и понятно почему: оно невыносимо скучно, и никому не требуется на практике. Так почему же люди думают, будто оно важно? Я не вижу, что пользы в том, что граждане носят в головах бледные воспоминания об алгебраических формулах и геометрических чертежах, и ясные воспоминания о том, как это все противно! С другой стороны, было бы куда полезнее показать им нечто прекрасное, дать им возможность стать творческими, гибкими умом мыслителями без предрассудков, — такими, какими их бы сделало настоящее математическое образование.

Симплицио. Но ведь люди же должны уметь деньги считать!

Сальвиати. Для этого калькуляторы есть. Почему бы ими не пользоваться? Куда как легче и вернее. Мой аргумент не только в том, что сегодняшняя система так ужасно плоха, но и в том, что она упускает нечто воистину чудесное! Математику следует преподавать как искусство во имя искусства, а «приземленные» полезные аспекты тривиально воспоследуют сами собою. Бетховен без труда бы написал песенку для рекламного ролика, но музыке ведь он учился, чтобы создавать прекрасные произведения!

Симплицио. Не каждый урожден художником. Как тогда быть с детьми, которые попросту «не математики»? Как они укладываются в твою схему?

Сальвиати. Если бы каждый был предоставлен математике в ее естественной форме, со всеми ее трудными радостями и удивлением познания, что она влечет за собою, думаю, мы бы были свидетелями драматического изменения отношения детей к математике, а взрослых — к тому, что означает быть «сильным по математике». Мы теряем столь многих несостоявшихся одаренных математиков — творцов, умниц, которые совершенно справедливо отвергают то, что видится им бессмысленным и выхолощенным предметом. Они попросту слишком умны, чтобы тратить время на такую чушь!

Симплицио. А тебе не кажется, что, будь уроки математики устроены подобно урокам рисования, так многие дети тогда бы вообще ничему не научились?

Сальвиати. Так они же ничему и не учатся! Лучше бы уж никаких уроков математики не было, чем такие! Пусть хоть кто-нибудь тогда смог бы открыть ее красоту для себя сам.

Симплицио. Так ты хочешь убрать математику из школьной программы?

Сальвиати. Ее давно убрали! Вопрос уже стоит о том, что делать с оставшейся от нее пустой засохшей шкуркой. Разумеется, я бы предпочел заменить ее исполненным радости, деятельным знакомством с математическими идеями.

Симплицио. Да много ли учителей знают свой предмет достаточно, чтоб так его преподавать?

Сальвиати. Мало, очень мало. И это лишь верхушка айсберга…

 

Математика в школе

 

Нет вернее способа убить энтузиазм детей и их интерес к предмету, чем включив его в обязательную часть школьной программы[10]. Включите его в ЕГЭ, и вы наверняка увидите, как образовательная бюрократия высосет все его жизненные соки. В отделах образования не понимают, что такое математика — как не понимают этого ни директора школ, ни авторы учебников, ни их издатели, ни — печальнее всего — учителя. Проблема столь велика, что я едва понимаю, с какого конца начать ее излагать.

Начнем с поражения множества реформ математического образования. Уже долгие годы все большее внимание уделяется разладу в системе математического образования. Оплачиваются исследования, собираются конференции, формируются бессчетные комитеты учителей, авторов и издателей учебников, чтобы «исправить ситуацию». Не упустив ни капли собственной издательской выгоды (на любые флуктуации политики обучения они отвечают предложением новых редакций своих нечитабельных уродищ), все эти реформаторы упустили главное: математическая программа должна быть не исправлена — она должна быть выброшена вон.

Вся эта болтовня и показуха касательно того, какие «пункты программы» и в каком порядке следует учить, использовать эту систему записи вместо той, какой модели калькулятор, Господи прости, нужен школьнику, — все это напоминает перестановку стульев на палубе тонущего «Титаника». Математика есть музыка разума. Заниматься математикой — значит совершать открытия и строить предположения; жить вдохновением и интуицией; значит оказываться в отчаянии — не потому, что предмет не имеет смысла, а потому, что вы придали ему смысл и все еще не понимаете, как ведет себя ваше создание; значит испытать и прорыв фонтана идей, и поражение художника; и в ужасе неметь от почти что физически невыносимого, переполняющего вас чувства прекрасного; да значит быть живым, черт побери! Уберите это из математики, и можете собирать сколько угодно умных конференций, и это ничего не изменит. Оперируйте, сколько хотите, дорогие доктора: пациент уже мертв.

Наипечальнейшая часть этих реформ — попытки «сделать математику интересной» и «важной в жизни детей». Вам не надо делать математику интересной — она уже более интересна, чем вы сможете вынести! И торжество ее в неважности для жизни — вот почему она так занимательна.

Попытки изобразить математику полезной и нужной для ежедневных дел всегда натужны и убоги: «Видите, дети, как просто, когда знаешь алгебру, высчитать, сколько Марии лет, если ей на два года больше, чем дважды ее возраст семь лет назад!» — как будто кто-то в жизни получит эту безумную информацию вместо настоящего возраста. Алгебра — не инструмент для жизни, это искусство симметрии и чисел, и потому достойно постижения само по себе.

Даны сумма и разность двух чисел. Каковы сами числа?

Вот простой, элегантный вопрос, и не надо лезть из кожи вон, чтобы придать ему привлекательности. Древние вавилоняне любили решать такие задачи, и наши ученики их тоже любят. (Да и вам, надеюсь, понравится!) Нам не надо заворачиваться в тройные узлы, чтобы придать математике важность для ежедневных дел. Ее важность, как и важность искусства вообще — в осмыслении человеческого опыта.

Или, может быть, вы думаете, что дети хотят чего-то, относящегося к их ежедневным делам? Может быть, их восхищает что-то практическое, например, сложный процент по кредиту? Людей восхищает фантазия, и это именно то, что математика может дать — убежище от ежедневного, волшебный бальзам от практических забот.

Другая проблема — когда авторы учебников начинают «сюсюкать», чтобы сделать математику «дружественной» и победить «страх перед математикой» (одна из множества болезней, на самом деле вызываемых школой). Чтобы ученики могли запомнить формулы, вы можете придумать целую историю о том, как Иван Демьянович едет на машине вокруг Елизаветы Макаровны и говорит ей, как хороши были ее два пирога (L=2πR), или что ее пироги квадратные (S=πR²), или еще какую-нибудь глупость. А как же настоящий рассказ о проблеме измерения кривых, о Евдоксе[11]и Архимеде и методе неделимых, о трансцендентности числа π? Что интереснее — измерять приблизительный размер кружка по клеточкам, а потом вычислять длину окружности по формуле, которую вам дали без объяснения, или услышать историю одной из самых прекрасных, захватывающих задач, и самых ярких и сильных идей всей человеческой истории? Мы убиваем в детях интерес к кругам, в конце концов!

Почему мы не даем ученикам услышать об этом, не то чтобы дать им возможность самим позаниматься математикой, прийти к собственным идеям и мнениям? Какой еще предмет изучают, даже не упоминая о том, каковы его история, философия, основоположения, эстетические критерии и текущее положение вещей? Какой еще предмет отбрасывает первоисточники — чудесных произведений искусства, выполненных самыми творческими умами истории — в пользу убогих третьесортных учебников?

Главная проблема школьной математики в том, что в ней нет задач. Да, я знаю, что выдается за задачи на уроках: эти безвкусные, скучные упражнения. «Вот задача. Вот как ее решить. Да, такие бывают на экзамене. На дом задачи 1—15». Что за тоскливый способ изучать математику: стать дрессированным шимпанзе.

Но задача — настоящий, честный до мозга костей естественный человеческий вопрос — это нечто другое. Какова длина диагонали куба? Закончатся ли простые числа? Бесконечность — число или нет? Сколькими способами можно симметрично покрыть поверхность плитками? История математики — это история решения этих вопросов, не бессмысленного пережевывания формул и алгоритмов, вместе с натянутыми упражнениями, чтобы их применять.

Хорошая задача — такая, решения которой вы не знаете. Вот где загадка, вот что дает настоящие возможности! Хорошая задача не стоит в отдельности, но служит стартовой площадкой для других интересных задач. Треугольник занимает половину описанного прямоугольника. А как насчет пирамиды в кубе? Можно ли эту задачу решить тем же способом?

Я принимаю идею обучения школьников технике решения, и я сам это делаю. Но это не цель. Техника в математике, как и в любом искусстве, должна изучаться в контексте. Великие задачи, их история, творческий процесс — вот этот контекст. Дайте ученикам хорошую задачу, пусть они поломают головы, пусть у них не получится ее решить. Посмотрите, что у них выйдет. Дождитесь до того момента, когда они страстно захотят свежую идею. Тогда научите их какой-то технике, только немного.

Отложите в сторону планы уроков и диапроекторы, мерзкие красочные учебники, компакт-диски и весь остальной парад уродов бродячего цирка, и займитесь с учениками математикой! Учителя живописи не тратят время на чтение учебников и зазубривание техники — они просто дают детям рисовать. Они ходят от мольберта к мольберту и подсказывают, направляют:

— Я думала о задаче с треугольником, и кое-что заметила. Смотрите, если треугольник наклонный, то он не занимает половины прямоугольника!

 

 

— Превосходное наблюдение! Наше рассуждение с рассечением треугольника предполагало, что вершина находится над основанием. Теперь нам нужна новая идея.

— Попытаться рассечь его иначе?

— Конечно. Попробуй всевозможные идеи. Расскажи потом, что у тебя выйдет!

Как же нам учить детей математике? Выбирая занимательные и естественные задачи, в соответствии с их вкусами, интересами и опытом. Давая им время делать открытия и строить гипотезы. Помогая им выстраивать доказательства и создавая атмосферу здорового и живого математического критицизма. Улавливая, куда меняется их интерес. В общем, выстраивая честные и открытые интеллектуальные отношения с учениками. Это требует слишком большой ответственности и слишком большой открытости — короче, это слишком много работы!

Гораздо проще быть пассивным передатчиком готовых школьных «материалов» и следовать инструкции, как на бутылке шампуня — «лекция, экзамен, повторить» — чем глубоко мыслить о собственном предмете и передавать этот смысл честно и наилучшим образом своим ученикам. Нас просто уговаривают забросить сложную задачу принятия решений своим умом и совестью, и вместо этого «проходить программу». Это попросту путь наименьшего сопротивления:

Выберите правильный ответ:

Авторы учебников относятся к учителям так же, как:

а) фармацевтические компании к докторам;

б) компании звукозаписи к диск-жокеям;

в) корпорации к депутатам

г) все вышеперечисленное.

Труд математики, как и живописи и поэзии, состоит в тяжелой творческой работе. Поэтому математику очень сложно преподавать. Математика — медленный созерцательный процесс. Изготовить произведение искусства занимает время, а, чтобы распознать его, нужен искусный учитель. Разумеется, легче вывесить список правил, чем вести за собой будущих художников, как легче написать инструкцию к телевизору, чем книгу со своей точкой зрения.

Математика — искусство, а искусство должно преподаваться действующими мастерами, или уж, по крайней мере, педагогами, любящими искусство и способными его распознать. Не обязательно учиться музыке у профессионального композитора, но отдадите ли вы ребенка в обучение кому-то, кто не умеет играть сам и не слышал ни одного музыкального произведения за всю жизнь? Возьмете ли вы учителем рисования того, кто не держал в руке карандаша и никогда не был в музее? Как же тогда мы допускаем в учителя математики того, кто не создал ни одного математического произведения, не знает ни истории, ни философии предмета, ни последних достижений математики, и ничего, в конце концов, из того, что он должен преподавать своим несчастным студентам? Что же это за учитель? Как они могут учить тому, чего сами не знают? Я не умею танцевать, но мне и в голову не придет, будто я могу вести танцевальный класс (хоть я мог б<

Поделиться:

Воспользуйтесь поиском по сайту: