Расчет линейных размерных цепей вероятностным методом.

Прямая задача

Назначить допуски и отклонения составляющих размеров с таким расчетом, чтобы обеспечить значение замыкающего размера равное А _∆= . Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0.21%.

На детали, входящие в сборочный комплект, назначены следующие значения номинальных размеров: N₁=15 мм, N₂=376 мм, N₃=37 мм, N₄=100 мм, N₅=180 мм, N₆=43 мм.

1.Согласно заданию

=1 мм

=0,5+0,8=1,3 мм

Е_{с ∆}=(0,5-0,8)/2=-0,15 мм

А _∆max=1+0,5=1,5 мм

А _∆min=1-0,8=0,2 мм

 

2.Составим график размерной цепи

 

3. Составим уравнение размерной цепи

 

+x₆A₆

 

Значения передаточных отношений

 

Обозначение передаточных отношений	ξ 1	ξ2	ξ 3	x4	x5	x6
Численное значение	-1	+1	-1	-1	-1	-1

 

4.Произведем проверку правильности назначения номинальных значений составляющих размеров:

=-21+376-37-100-180-43=1 мм

Так как по условию задачи =1 мм, следовательно, номинальные размеры

назначены правильно.

5.Осуществим увязку допусков, для чего исходя из величины , рассчитаем допуски составляющих размеров.

Так как в узел входят подшипники качения, допуски которых уже являются заданными, то для определения величины воспользуемся зависимостью

 

6.Устанавливаем для всех размеров допуски по 12 квалитету, тогда Т₁=0,18 мм, Т₂=0,57 мм, Т₃=0,12 мм, Т₄=0,35 мм, Т₅=0,4 мм, Т₆=0,12 мм,

7.Произведем проверку правильности назначения допусков составляющих размеров по уравнению

(1)

 

мм

 

Полученная сумма допусков оказалась меньше заданного допуска замыкающего размера. Для того чтобы полностью использовать заданный допуск замыкающего размера, увеличим допуск размера А₅ и найдем его из уравнения (1)

8.Осуществим увязку средних отклонений. Увязку будем производить за счет среднего отклонения размера А₅, принятого в качестве увязачного.

Примем следующий характер расположения полей допусков составляющих размеров

А₁=15Js12( 0,09)

А₂=376Js12( 0,285)

А₃=37(_-0.12)

А₄=100h12(_-0.35)

А₅=180h12(_-0.4)

А₆=43(_-0.12)

 

Сведем данные для расчета в таблицу

Обозначение размера	Размер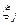
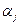
А1	15Js12( 0,09)	-1		0,18
А2	376Js12( 0,285)	+1		0,57
А3	37(-0.12)	-1	-0,06	0,12	+0,2	0,012	-0,048	0,048
А4	100h12(-0.35)	-1	-0,175	0,35	+0,2	0,035	-0,14	0,14
А5		-1	Ec5	0,815	+0.2	0,0815	Ec5+0,0815	-Ec5-0,0815
А6	43(-0.12)	-1	-0,06	0,12	+0.2	0,012	-0,048	0,048

Таблица расчетных данных

 

По уравнению найдем среднее отклонение размера А₅.

-0,15=0,048-E_c5-0,0815+0,14+0,048

Е_с5=0,3045 мм

Предельные отклонения размера А₅:

ES₅=0,3045+0,5*0,815=0,712 мм

EI₅=0,3045-0,5*0,815=-0,103 мм

Т.о.

А₅= мм

 

Расчет линейных размерных цепей вероятностным методом.

Обратная задача

Найти предельные значения замыкающего размера при значениях замыкающих размеров, полученных в результате решения примера 3.

Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0.21%.

Сведем данные для расчета в таблицу

Обозначение размера	Размер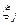
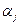
А1	15Js12( 0,09)	-1		0,18					0,18	0,0324
А2	376Js12( 0,285)	+1		0,57					0,57	0,3249
А3	37(-0.12)	-1	-0,06	0,12	+0,2	0,012	-0,048	0,048	0,12	0,0144
А4	100h12(-0.35)	-1	-0,175	0,35	+0,2	0,035	-0,14	0,14	0,35	0,1225
А5		-1	0,3045	0,815	+0,2	0,0815	0,386	-0,386	0,815	0,664
А6	43(-0.12)	-1	-0,06	0,12	+0,2	0,012	-0,048	0,048	0,12	0,0144

 

1. Номинальное значение замыкающего размера:

=-15+376-37-100-180-43=1 мм

2. Среднее отклонение замыкающего размера

Е _с∆=0+0+0,048+0,14-0,386+0,048=-0,15 мм

 

3.Допуск замыкающего размера

Т _∆=1,2 =1,29966»1,3 мм

 

4.Предельные значения замыкающего размера

А _∆max=1-0,15+0.5∙1,3=1,5 мм

А _∆min=1-0,15-0.5∙1,3=0,2 мм

 

 

5.Сравним полученные результаты с заданными

А _{∆max расч}=1,5 мм = А _{∆max зад}=1,5 мм

А _{∆min расч}=0,2 мм = А _{∆min зад}= 0,2 мм

 

Следовательно, изменения предельных отклонений составляющих размеров не требуется.

Часть 3.

 

 

Решение.

1. Определяем среднее арифметическое и стандартное отклонение для данных таблицы 5:

(3.1)

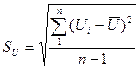(3.2)

 

2. С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.

Таким образом, ни один из результатов не выходит за границы интервала , следовательно, с вероятностью 0,9973 гипотеза об отсутствии грубых погрешностей принимается.

 

3. Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Для этого разбиваем вариационный ряд значений напряжения (таблица 1) на 11 интервалов.

Рассчитываем значение интервалов по формуле (3.3).

, (3.3)

где k – число интервалов.

Примем k=10

.

Выбираем начало первого интервала равным

Конец последнего (10 интервала) в точке

Затем для каждого интервала подсчитывается количество результатов , попавших в данный интервал и определяется

(3.4)

Результаты производимых вычислений заносятся в таблицу 6.

 

 

Таблица 6.

№	Uj-1	Uj	mj	zj	Ф(zj)	Pj	mj-nPj	Χ²j
	-	33,21291		-		0,006	-0,6	0,6
	33,21291	33,33446		-2,24998	0,0123	0,0063	1,37	2,979206
	33,33446	33,45601		-1,49996	0,0668	0,0545	-1,45	0,38578
	33,45601	33,57756		-0,74995	0,22662	0,15982	-1,982	0,245797
	33,57756	33,69911		6,17E-05	0,5	0,27338	4,662	0,79502
	33,69911	33,82066		0,750074	0,7734	0,2734	-3,34	0,408032
	33,82066	33,94221		1,500086	0,9332	0,1598	1,02	0,065106
	33,94221	34,06376		2,250099	0,9877	0,0545	0,55	0,055505
	34,06376	34,18531		3,000111	0,9986	0,0109	-0,09	0,007431
	34,18531	-		-		0,0014	-0,14	0,14

 

Затем строится гистограмма (рис.1). При построении гистограммы выбираем масштаб таким образом, чтобы высота относилась к основанию как 5 к 8.

 

 

Рис. 1 Гистограмма

Из вида гистограммы на рис 1 можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

4. Проверка нормальности закона распределения по критерию Пирсона.

Если выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используется функция Лапласа по формуле (3.5)

,(3.5)

где значения и соответствуют началу и концу интервала соответственно. При этом учитываем, что конец предыдущего интервала является началом следующего интервала. Для каждого из этих значений рассчитаем относительный доверительный интервал по формуле (3.6)

,(3.6)

а затем из таблиц функции Лапласа найдем соответственные значения и

. Данные заносим в таблицу 2.

Находим доверительную вероятность для каждого интервала по формуле (3.7).

(3.7)

Затем рассчитаем значение и найдем суммарное значение

Данные расчета занесем в таблицу 2.

Определим табличное (критическое) значение , задавшись доверительной вероятностно 0,92 и вычислив по формуле r = k - 3 число степеней свободы:

.

.

Таким образом, с вероятностью 0,92 гипотеза о нормальности распределения вероят­ности результата измерения напряжения принимается.

5. В тех же координатах, что и гистограмма, строим теоретическую кри­вую плотности вероятности. Для этого рассчитываем значения плотности вероятности для середины каждого интервала . Результат расчета заносим в таблицу 2. Эти значения откладываем как ординаты из середин соответ­ствующих интервалов; полученные точки соединяем плавной кривой, симметричной отно­сительно математического ожидания (среднего арифметического значения) (рис.1).

 

6. Представление результата в виде доверительного интервала.

Для этого определим стандартное отклонение среднего арифметического по формуле (3.8):

,(3.8)

.

 

Закон распределения вероятности для среднего арифме­тического считаем нормальным (что следует из нормальности распределения самой изме­ряемой величины), тогда доверительный интервал определяем по выражению 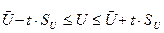, при до­верительной вероятности 0,92. Этому значению соответствует аргумент функции Лаплапса t = 1,771.

 

Так как закон распределения вероятности для среднего арифметического счи­тается неизвестным, то относительный доверительный интервал рассчитываем в соответст­вии с неравенством Чебышева (3.9):

(3.9)

,

Как видно из сравнения результатов, неизвестность закона распределения вероятно­сти приводит к расширению доверительного интервала, то есть к увеличению дефицита из­мерительной информации.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: