 |
Модель идеализированного p-n-перехода
|
|
|
|
Одной из простых моделей полупроводникового диода является математическая модель идеализированного p-n -перехода, пригодная для расчёта принципиальных электрических схем в диапазоне низких и средних частот, когда режим работы диода можно считать квазистатическим.
Для идеализированного p-n -перехода (рис. 1.2) приняты следующие допущения [2]:
1) в обеднённом слое отсутствуют генерация, рекомбинация и рассеяние носителей зарядов,
2) носители зарядов проходят через обеднённый слой мгновенно, т.е. предполагается, что токи носителей заряда одного знака одинаковы на обеих границах перехода,
3) электрическое поле вне обеднённого слоя отсутствует, т.е. полупроводник вне перехода остаётся электрически нейтральным и здесь носители заряда движутся только за счёт диффузии,
4) сопротивления нейтральных p - и n -областей пренебрежимо малы по сравнению с сопротивлением обеднённого слоя, т.е. можно считать, что всё внешнее напряжение практически полностью приложено к обеднённому слою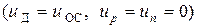 
,
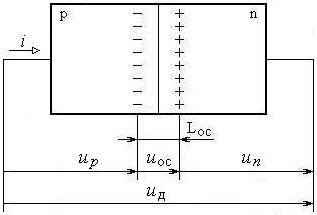
Рис. 1.2. Структура p-n -перехода (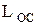
− ширина обеднённого слоя)
5) низкий уровень инжекции зарядов,
6) границы обеднённого слоя плоскопараллельные, а носители зарядов перемещаются по направлению, перпендикулярному этим плоскостям, то есть концентрации носителей зависят только от одной координаты.
В этом случае вольтамперная характеристика идеализированного p-n -перехода описывается формулой Шокли:
где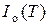 
− тепловой обратный ток p-n-перехода,
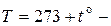температура p-n -перехода, обычно принимаемая равной температуре окружающей среды 
,
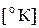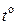− температура окружающей среды [ 
],
− напряжение между выводами идеализированного диода,
− термический потенциал [В],
|
|
|
− температурный потенциал,
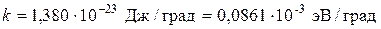− постоянная Больцмана,
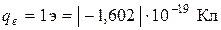− заряд электрона.
Ток 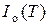назван тепловым, потому что, во-первых, он обусловлен тепловой генерацией неосновных носителей в нейтральных p - и n -областях, прилегающих к p-n -переходу, и, во-вторых, его значение сильно зависит от температуры p-n -перехода.
Функцию 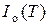характеризуют температурой удвоения 
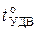, т.е. приращением температуры окружающей среды, которое вызывает удвоение обратного тока p-n -перехода 
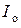, заданного в справочнике при температуре 
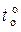, т.е. при температуре 
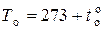. Иногда в качестве 
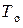принимают среднюю температуру рабочего диапазона.
Температуру удвоения можно рассчитать по формуле
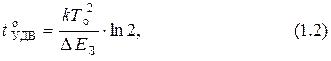
где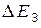 
− ширина запрещённой зоны полупроводника (для Si 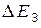= 1,12 эВ, для Ge 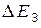= 0,66 эВ). Для кремния при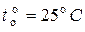 
.
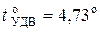С учётом изложенного можно записать выражение
Здесь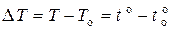 
.
Для реальных диодов температура удвоения много больше рассчитанной теоретически и может составлять десятки градусов. Поэтому 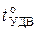следует находить по справочным данным для конкретного типа диода.
Вольтамперная характеристика (ВАХ) идеализированного p-n -перехода приведена на рис. 1.3. Ветвь ВАХ при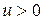 
называют прямой, а при 
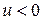− обратной.
Первое слагаемое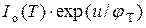 
в формуле (1.1) является диффузионной составляющей тока диода, второе 
− дрейфовой. При прямом напряжении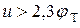 
дрейфовой составляющей можно пренебречь и поэтому вместо формулы (1.1) пользоваться упрощенной формулой
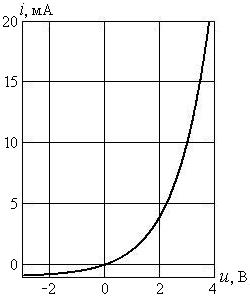
Рис. 1.3. Вольтамперная характеристика полупроводникового диода с идеализированным p-n -переходом
Статическое сопротивление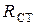 
полупроводникового диода (сопротивление постоянному току) можно найти по закону Ома из формулы (1.1):
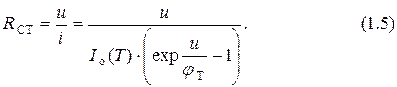
При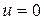 
статическое сопротивление следует рассчитывать по формуле 
. Зависимость 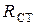от напряжения между выводами диода приведена на рис. 1.4.
Таким образом, идеальный p-n -переход может быть заменён нелинейным сопротивлением 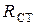. Однако в качестве эквивалентной схемы идеального p-n -перехода (идеального диода) принято использовать условное графическое изображение полупроводникового диода VD (рис. 1.1 а).
|
|
|
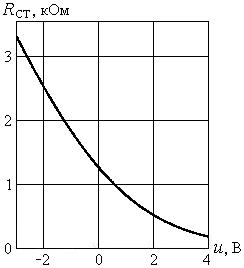
Рис. 1.4. Типовая зависимость статического сопротивления от напряжения на диоде
Эта схема позволяет указывать движение тока в прямом направлении от анода к катоду и правильно пользоваться уравнением (1.1).
[1] Данный раздел студенты изучают самостоятельно
|
|
|
12 |
