Расчёт рабочей точки полупроводникового диода в

ЛЕКЦИЯ 2

 

Полупроводниковые диоды

 

План лекции:

Математические модели и эквивалентные схемы реальных полупроводниковых диодов

Расчёт рабочей точки полупроводникового диода в статическом режиме

 

Математические модели и эквивалентные схемы реальных

Полупроводниковых диодов

2.1.1. Модель реального p-n -перехода в статическом режиме работы

В реальном p-n -переходе в обеднённом слое имеют место как генерация, так и рекомбинация носителей зарядов, т.е. первое допущение, принятое для идеализированного p-n -перехода, не выполняется. В этом случае вольтамперную характеристику диода описывают формулой, в которую вводят коэффициент 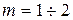, учитывающий неидеальность обеднённого слоя:

Так как нелинейными свойствами обладает обеднённый слой, то собственно неидеальность p-n -перехода можно выразить как

Кроме того, электрические сопротивления и нейтральных p - и n -областей хотя и малы относительно 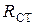, но достаточно велики по абсолютной величине и могут составлять единицы и даже десятки Ом. Поэтому ими пренебрегать нельзя, как это сделано в третьем допущении, а эквивалентная схема замещения реального полупроводникового диода (рис. 2.1) будет отличаться от схемы идеального диода.

Суммарное сопротивление , учитывающее свойства нейтральных p - и n -областей, называют базовым сопротивлением диода.

 

Рис. 2.1. Структура (а) и эквивалентная схема реального полупроводникового диода с p-n -переходом (б)

 

На базовом сопротивлении при протекании тока имеет место падение напряжения . Поэтому формула (2.1) может быть преобразована к виду

Вольтамперная характеристика полупроводникового диода с реальным p-n -переходом приведена на рис. 2.2.

С ростом прямого тока падение напряжения на базовой области диода может стать сравнимым с напряжением на p-n -переходе, т.е. . При этом на ВАХ диода появится почти линейный участок. При дальнейшем увеличении прямого тока сопротивление начинает уменьшаться из-за увеличения концентрации инжектированных в базу носителей заряда. ВАХ снова начнёт отклоняться от прямой линии. Это явление называют эффектом модуляции сопротивления базы. Однако данный эффект учитывать не будем.

 

Рис. 2.2. Вольтамперная характеристика полупроводникового диода (1 − с идеализированным p-n -переходом, 2 – с учётом неидеальности () обеднённого слоя, 3 – с реальным p-n -переходом)

 

Величины и непосредственно в справочных данных не приводят. Поэтому значения этих параметров надо вычислять по формуле (2.3), используя семейство характеристик , приводимых в отдельных справочниках в виде графиков для конкретного типа диода.

 

2.1.2. Модели идеализированного и реального p-n -переходов в динамическом режиме работы

В динамическом режиме работы важную роль играют дифференциальное сопротивление и ёмкость p-n -перехода.

Дифференциальное сопротивление представляет собой величину, обратную крутизне вольтамперной характеристики p-n -перехода.

Преобразуя формулу (2.1) для идеализированного p-n -перехода к виду

получаем выражение

Здесь и в дальнейшем для простоты будем обозначать как .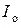

Для реального p-n -перехода из преобразованной формулы (2.2) имеем

и выражение

При дифференциальное сопротивление больше статического, а при имеет место обратное соотношение (рис. 2.3).

 

Рис. 2.3. Сравнительные характеристики статического и дифференциального сопротивлений полупроводникового диода

 

Границами обеднённого слоя являются равные по величине, но противоположные по знаку электрические заряды ионов акцепторов и доноров. Между границами существует разность потенциалов 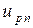или потенциальный барьер. Поэтому по определению эта область p-n -перехода обла­дает ёмкостью, называемой барьерной:

Здесь − значение барьерной ёмкости при , 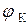− контактная разность потенциалов, которую можно принять равной , 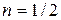для резкого p-n -перехода и для плавного p-n -перехода.

Кроме того, в реальном p-n -переходе в p - и n -областях имеются движущиеся заряды, а на сопротивлениях и имеет место падение напряжений. Следовательно, существует ещё одна ёмкость, называемая диффузионной, так как заряды в p - и n -областях движутся благодаря диффузии.

Барьерная и диффузионная емкости составляют ёмкость реального p-n -перехода, причём . Несмотря на то, что ёмкости образованы в разных частях p-n -пере­хода, в эквивалентной схеме они объединены в одну, параллельную реальному (неидеальному диоду) − рис. 2.4 а.

 

Рис. 2.4. Эквивалентные схемы реального p-n -пере­хода (а) и реального полупроводникового диода (б) в динамическом режиме работы (диапазон высоких частот)

Реальный диод как конструктивный элемент схемы обладает паразитной ёмкостью корпуса и паразитной индуктивностью выводов. В диапазоне высоких частот паразитной индуктивностью можно пренебречь (рис. 2.4 б), а в диапазоне сверхвысоких частот необходимо учитывать оба паразитных параметра (рис. 2.5).

 

Рис. 2.5. Эквивалентная схема реального полупроводникового диода в динамическом режиме работы (диапазон свч)

 

Расчёт рабочей точки полупроводникового диода в

Статическом режиме

Типовая принципиальная электрическая схема включения полупроводникового диода в цепь постоянного тока приведена на рис. 2.6.

В качестве исходных параметров могут быть заданы, например, величина эдс ,внутреннее сопротивление 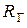источника эдс, сопротивление нагрузки и температура окружающей среды .

 

Рис. 2.6. Схема цепи постоянного тока с полупроводниковым диодом

Требуется выбрать марку диода и рассчитать его рабочую точку, то есть ток в цепи и напряжение на диоде 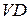. Обычно также требуется найти напряжение на нагрузке.

Так как общим элементом цепи является ток, то должно выполняться условие равенства токов, протекающих через диод и через нагрузку:

Данная задача является нелинейной, выражается через трансцендентную функцию и может быть решена только численными методами.

Для обеспечения высокой точности получаемого результата необходимо задать абсолютную погрешность нахождения тока в рабочей точке или разности напряжений .

По первому закону Кирхгофа составим уравнение электрической цепи

где − падение напряжения на внутреннем сопротивлении источника эдс, – напряжение на диоде, – напряжение на нагрузке.

Разделим знаком равенства линейную и нелинейную части уравнения:

Левая часть этого выражения

является линейной зависимостью между током и напряжением и носит название нагрузочной прямой.

Для построения графической зависимости 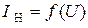запишем уравнение нагрузочной прямой в более удобном виде:

Здесь .

Правая часть выражения (2.11) представляет собой вольтамперную характеристику диода в виде нелинейной зависимости

где , а второе слагаемое есть напряжение .

Графики уравнений (2.13) и (2.14) позволяют наглядно представить решение нелинейного уравнения (2.11) и увидеть рабочую точку (рис. 2.7). Графическое решение не обеспечивает нужную точность, но даёт возможность предложить варианты расчёта рабочей точки.

 

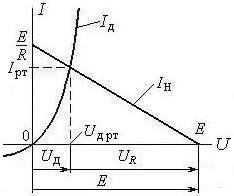
Рис. 2.7. Графическое решение нелинейного уравнения (2.11)

 

На первом этапе любого из возможных алгоритмов численного решения задачи нахождения рабочей точки осуществляют вручную выбор подходящего полупроводникового диода и его исходных данных для расчёта его параметров в дальнейшем с помощью ЭВМ.

Поделиться:

Воспользуйтесь поиском по сайту: