 |
Выбор полупроводникового диода и нахождение его параметров
|
|
|
|
ЛЕКЦИЯ 4
Расчёт выпрямителей
План лекции:
Однополупериодный выпрямитель с ёмкостной нагрузкой
Двухполупериодный выпрямитель с ёмкостной нагрузкой
Однополупериодный выпрямитель с ёмкостной нагрузкой
Рассмотрим работу цепи переменного тока низкой частоты с полупроводниковым диодом, нагрузкой которого является параллельное соединение резистора и ёмкости (рис. 4.1).
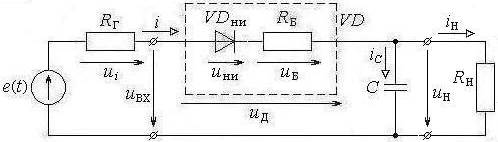
Рис. 4.1. Эквивалентная схема электрической цепи переменного тока с полупроводниковым диодом и емкостной нагрузкой
Наиболее часто в цепи действует гармоническая эдс
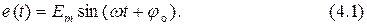
В диапазоне низких частот (как правило, до 1÷1,5 кГц) такую простейшую схему однополупериодного выпрямителя с ёмкостной нагрузкой используют в качестве источника постоянного напряжения как источника питания аппаратуры.
Основными выходными параметрами выпрямителя являются среднее значение выпрямленного выходного напряжения  , коэффициент пульсаций
, коэффициент пульсаций  и среднее значение тока через нагрузку
и среднее значение тока через нагрузку 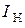 . Здесь
. Здесь  .
.
В диапазонах средних и высоких частот (более 100 кГц) эту схему используют в качестве амплитудного детектора для выделения огибающей амплитудно-модулированного сигнала. В этом случае основным выходным параметром схемы является минимум нелинейных искажений огибающей.
Существуют инженерные методики расчёта выпрямителя и амплитудного детектора в установившемся режиме работы по средним показателям. Однако весьма интересными являются переходные процессы, расчёт которых очень труден и возможен только методами дискретной математики с использованием современных ЭВМ.
Качественно переходный процесс в выпрямителе с ёмкостной нагрузкой можно представить следующей моделью.
|
|
|
Предположим, что напряжение на ёмкости отсутствует. После включения эдс в цепь первая положительная полуволна напряжения отпирает диод и через него начинает проходить ток, часть которого протекает через сопротивление нагрузки, а другая часть через ёмкость, заряжая её. На спаде положительной полуволны, когда напряжение эдс сравнивается с напряжением на ёмкости, диод запирается и начинается разряд ёмкости через сопротивление нагрузки. Разряд продолжается до тех пор, пока входное напряжение отрицательно и пока положительное напряжение второй полуволны не превысит напряжение на ёмкости (рис. 4.2).
За время одного периода напряжение на ёмкости не успевает достичь своего максимального значения. Поэтому в следующий положительный полупериод волны эдс, когда диод находится в открытом состоянии, ёмкость успевает зарядиться до большей величины. Затем диод запирается и начинается новый разряд ёмкости через сопротивление нагрузки. Процесс заряда-разряда продолжается непрерывно, пока в цепи действует эдс.
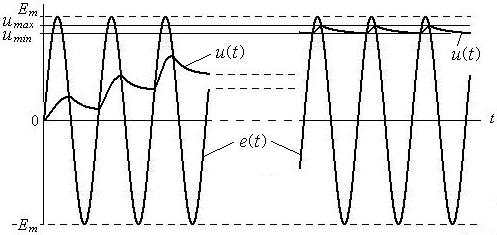
Рис. 4.2. Переходный процесс в однополупериодном выпрямителе
От периода к периоду время заряда ёмкости уменьшается, а разряда увеличивается. Соответственно прирост напряжения уменьшается, а спад увеличивается. Однако в среднем напряжение на ёмкости постепенно растёт.
Процесс увеличения среднего значения выходного напряжения продолжается до тех пор, пока за один период эдс прирост напряжения не становится равным спаду. Выпрямитель переходит в установившийся режим работы, когда постоянное выходное напряжение несколько меньше амплитуды эдс и колеблется около своего среднего значения. Для получения малых пульсаций постоянная времени фильтра 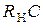 должна быть много больше периода гармонической эдс, чтобы за то время, когда диод закрыт, напряжение на ёмкости уменьшалось мало и обеспечивало требуемый коэффициент пульсаций.
должна быть много больше периода гармонической эдс, чтобы за то время, когда диод закрыт, напряжение на ёмкости уменьшалось мало и обеспечивало требуемый коэффициент пульсаций.
|
|
|
Напряжение на ёмкости по отношению к диоду включено в обратном направлении. Поэтому при отрицательном полупериоде эдс к диоду приложено обратное напряжение величиной 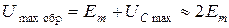 .
.
Перед началом работы выпрямителя ёмкость разряжена, напряжение на ней равно нулю и сопротивление ёмкости
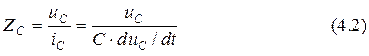
также равно нулю.
Следовательно, в момент включения эдс 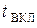 всё входное напряжение практически оказывается приложенным к диоду и через него начинает протекать ток, зависящий от величины эдс в этот момент
всё входное напряжение практически оказывается приложенным к диоду и через него начинает протекать ток, зависящий от величины эдс в этот момент
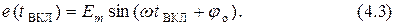
Весьма часто начальный ток может превышать максимально допустимую для диода величину, что может привести к пробою диода и выходу выпрямителя из строя. Поэтому наиболее важным и интересным с точки зрения расчёта переходного процесса является момент включения эдс и ближайшее после этого время.
Из формулы (4.2) следует, что с ростом напряжения 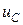 сопротивление ёмкости возрастает по двум причинам.
сопротивление ёмкости возрастает по двум причинам.
Во-первых, за счёт роста напряжения на ёмкости при её заряде, то есть из-за увеличения числителя.
Во-вторых, за счёт уменьшения скорости роста напряжения на ёмкости, то есть из-за уменьшения знаменателя. Рост напряжения на ёмкости уменьшает падение напряжения на диоде, что уменьшает ток, протекающий через диод, и соответственно скорость нарастания напряжения на ёмкости.
Задача расчёта переходных процессов в выпрямителе с ёмкостной нагрузкой формулируется следующим образом: по заданным параметрам выбрать диод, рассчитать величину ёмкости фильтра, необходимую амплитуду эдс 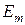 , обеспечивающую получение заданных значений
, обеспечивающую получение заданных значений 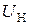 ,
, 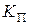 ,
, 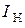 , рассчитать зависимости
, рассчитать зависимости 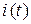 ,
, 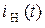 ,
,  и
и 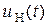 от времени и построить их.
от времени и построить их.
Наличие ёмкости приводит к тому, что нелинейное уравнение электрической цепи становится нелинейным дифференциальным, решение которого намного сложнее решения просто нелинейного уравнения.
Из-за наличия ёмкости схема становится инерционной, так как требуется время для изменения напряжения на ёмкости. Поэтому данную задачу графически решить нельзя.
Составим систему уравнений цепи по первому и второму законам Кирхгофа

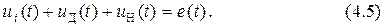
Здесь 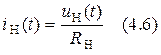 ,
, 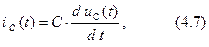
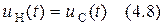 ,
, 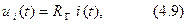
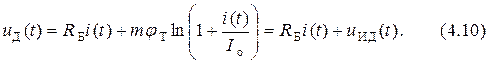
Используя приведённые формулы, выразим уравнение (4.5) через напряжение 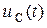 :
:
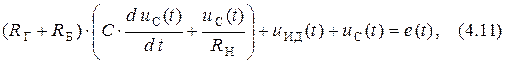
где 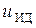 − напряжение на p-n -переходе (на идеальном диоде).
− напряжение на p-n -переходе (на идеальном диоде).
|
|
|
Решить уравнение (4.11) можно только численными методами, так как найти аналитическое решение невозможно.
Численные методы предполагают пошаговое решение уравнений. А для этого необходимо выбрать достаточно малый отрезок времени 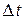 и последовательно вычислять значения функции в точках, расположенных друг от друга через
и последовательно вычислять значения функции в точках, расположенных друг от друга через 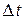 в выбранном интервале времени от
в выбранном интервале времени от 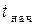 до
до 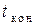 .
.
При малом 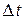 практически любую зависимость можно представить ломаной кривой, образованной либо прямыми отрезками между концами интервалов
практически любую зависимость можно представить ломаной кривой, образованной либо прямыми отрезками между концами интервалов 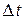 , либо средними значениями функции в интервалах
, либо средними значениями функции в интервалах  . Такой подход позволяет получить аналитические выражения, пригодные для вычисления значений функций с достаточной точностью.
. Такой подход позволяет получить аналитические выражения, пригодные для вычисления значений функций с достаточной точностью.
В выпрямителе диод работает в низкочастотном диапазоне, поэтому паразитными ёмкостями в эквивалентной схеме диода можно и нужно пренебречь. Следовательно, диод представляет собой нелинейное активное сопротивление
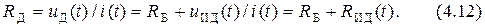
Замена нелинейного сопротивления  p-n -перехода в интервале
p-n -перехода в интервале 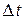 постоянным сопротивлением
постоянным сопротивлением  преобразует нелинейное дифференциальное уравнение (4.11) в линейное
преобразует нелинейное дифференциальное уравнение (4.11) в линейное

решение которого может быть найдено в аналитической форме.
Решение проще искать, если объединить последовательно соединённые сопротивления в одно 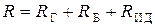 (рис. 4.3).
(рис. 4.3).
С учётом принятых обозначений после приведения подобных членов уравнение (4.13) будет записано как
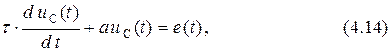
где 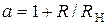 − постоянный коэффициент в пределах
− постоянный коэффициент в пределах 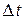 ,
, 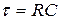 − постоянная времени контура
− постоянная времени контура  .
.

Рис. 4.3. Эквивалентная схема однополупериодного выпрямителя с ёмкостной нагрузкой
Уравнение (4.14) в операторной форме для гармонической эдс (4.1) имеет вид
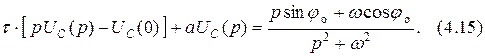
Преобразуя его относительно искомой величины 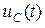 и решая, получаем
и решая, получаем
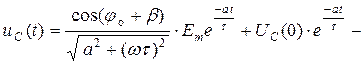
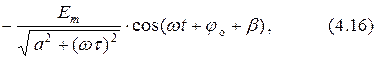
где 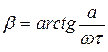 .
.
Решение справедливо при условии, что сопротивление 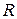 постоянно.
постоянно.
Пусть в качестве исходных параметров заданычастота 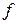 и начальная фаза
и начальная фаза  гармонической эдс
гармонической эдс 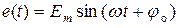 , внутреннее сопротивление
, внутреннее сопротивление 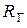 источника эдс, выходное напряжение
источника эдс, выходное напряжение 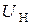 , коэффициент пульсаций
, коэффициент пульсаций 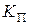 , выходной ток
, выходной ток 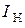 и температура окружающей среды
и температура окружающей среды 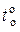 .
.
Как обычно, решение задачи начинается с подготовки исходных данных, а именно с выбора полупроводникового диода и нахождения его параметров для расчёта необходимых характеристик.
|
|
|
Выбор полупроводникового диода и нахождение его параметров
Диод выбирают из условий  и
и  .
.
Далее по справочным данным выбирают две температуры  и
и  , для которых приведены графические зависимости обратного тока
, для которых приведены графические зависимости обратного тока 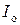 от обратного напряжения
от обратного напряжения 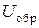 и прямого (среднего) тока
и прямого (среднего) тока 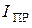 от прямого напряжения
от прямого напряжения 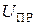 .
.
Для 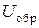 , близкого к максимальному значению на графике, определяют обратные токи p-n -перехода
, близкого к максимальному значению на графике, определяют обратные токи p-n -перехода  и
и  при температурах
при температурах  и
и 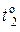 соответственно.
соответственно.
Для 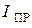 , близкого к максимальному значению на графике, определяют прямые напряжения
, близкого к максимальному значению на графике, определяют прямые напряжения 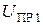 и
и 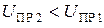 при температурах
при температурах  и
и 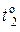 соответственно.
соответственно.
Ввод исходных данных
Алгоритм решения поставленной задачи начинается с ввода исходных данных (рис. 4.4, символ 1).
Вначале вводят требуемые параметры выпрямителя: 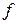 ,
,  ,
, 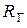 ,
, 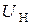 ,
, 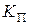 ,
, 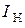 и
и 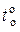 .
.
Затем вводят параметры диода: 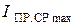 ,
, 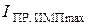 ,
, 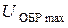 ,
, 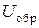 ,
,  ,
, 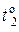 ,
,  ,
, 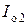 ,
, 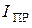 ,
, 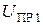 ,
, 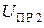 .
.
Вводят дополнительные данные для расчёта: 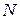 − количество расчётных точек за период гармонического сигнала (для получения достаточно высокой точности следует выбирать число точек из условия
− количество расчётных точек за период гармонического сигнала (для получения достаточно высокой точности следует выбирать число точек из условия 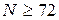 ), М − количество периодов,
), М − количество периодов, 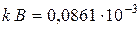 эВ / град – постоянную Больцмана,
эВ / град – постоянную Больцмана, 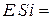 = 1,12 эВ – ширину запрещённой зоны для кремния,
= 1,12 эВ – ширину запрещённой зоны для кремния, 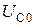 − начальное напряжение на ёмкости, относительную погрешность нахождения выходного напряжения (например,
− начальное напряжение на ёмкости, относительную погрешность нахождения выходного напряжения (например, 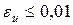 ).
).
3. Расчёт начальных значений величин (рис. 4.4, символ 2)
Рассчитывают:
1) 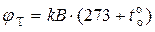 − температурный потенциал,
− температурный потенциал,
2) 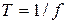 – период эдс,
– период эдс,
3) 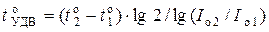 − температуру удвоения обратного тока p-n -перехода,
− температуру удвоения обратного тока p-n -перехода,
4) 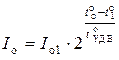 − обратный ток p-n -перехода при температуре
− обратный ток p-n -перехода при температуре 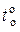 ,
,
5) 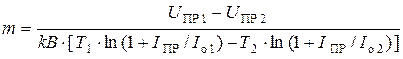 − коэффициент неидеальности обеднённого слоя,
− коэффициент неидеальности обеднённого слоя,
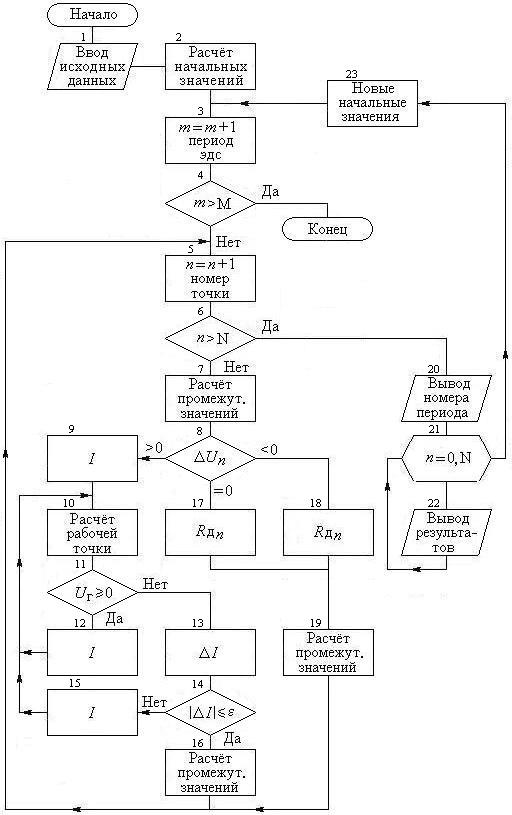
Рис. 4.4. Схема алгоритма расчёта выпрямителя, работающего на ёмкостную нагрузку
6) 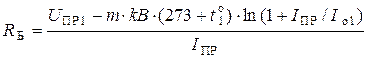 − базовое сопротивление диода,
− базовое сопротивление диода,
7) 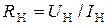 − сопротивление нагрузки,
− сопротивление нагрузки,
8)  − ёмкость выпрямителя,
− ёмкость выпрямителя,
9) 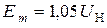 − амплитуду эдс (первое приближение),
− амплитуду эдс (первое приближение),
10) 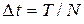 − шаг по времени,
− шаг по времени,
11) 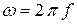 − угловую частоту эдс,
− угловую частоту эдс,
12) 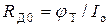 − эквивалентное сопротивление диода при нулевых начальных условиях,
− эквивалентное сопротивление диода при нулевых начальных условиях,
13)  − начальная величина суммарного сопротивления,
− начальная величина суммарного сопротивления,
14) 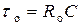 − начальное значение постоянной времени контура
− начальное значение постоянной времени контура  ,
,
15) 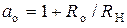 − начальное значение коэффициента
− начальное значение коэффициента 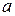 ,
,
16) 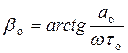 − начальное значение
− начальное значение 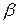 ,
,
17) 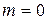 ,
, 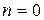 − начальные значения счётчиков номера цикла и номеров точек.
− начальные значения счётчиков номера цикла и номеров точек.
4. Начало цикла расчётов и проверка достижения окончания расчётов (рис. 4.4, символы 3 и 4)
5. Начало цикла расчётов переходного процесса и проверка достижения окончания расчёта точек в пределах одного периода (рис. 4.4, символы 5 и 6)
6. Расчёт промежуточных значений электрических величин (рис. 4.4, символ 7)
Рассчитывают:
1) 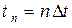 − время в текущей точке,
− время в текущей точке,
|
|
|
2) 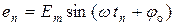 − эдс в текущей точке,
− эдс в текущей точке,
3) 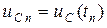 − выходное напряжение в текущей точке по формуле (4.16),
− выходное напряжение в текущей точке по формуле (4.16),
4) 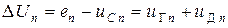 − разность напряжений, равная сумме напряжений на внутреннем сопротивлении источника эдс и диоде в текущей точке.
− разность напряжений, равная сумме напряжений на внутреннем сопротивлении источника эдс и диоде в текущей точке.
7. Оценка разности напряжений (рис. 4.4, символ 8)
Если 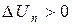 , то рассчитывают примерную величину тока через диод
, то рассчитывают примерную величину тока через диод 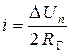 (рис. 4.4, символ 9) и переходят к расчёту рабочей точки (символы 10 и далее).
(рис. 4.4, символ 9) и переходят к расчёту рабочей точки (символы 10 и далее).
Если 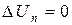 , то это означает, что диод закрыт, его сопротивление
, то это означает, что диод закрыт, его сопротивление 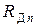 принимают равным
принимают равным 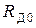 (символ 17) и переходят к символу 19.
(символ 17) и переходят к символу 19.
Если 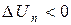 , то это также означает, что диод закрыт, но его сопротивление
, то это также означает, что диод закрыт, но его сопротивление 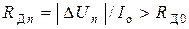 (символ 18). Далее переходят к символу 19.
(символ 18). Далее переходят к символу 19.
8. Цикл расчёта рабочей точки (рис. 4.4, символ 10)
Рассчитывают:
1) 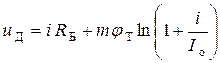 − напряжение на диоде,
− напряжение на диоде,
2) 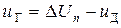 − напряжение на внутреннем сопротивлении источника эдс,
− напряжение на внутреннем сопротивлении источника эдс,
3)  − ток через источник эдс.
− ток через источник эдс.
Определение знака напряжения 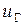 (символ 11).
(символ 11).
Если 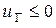 , то уменьшают ток
, то уменьшают ток 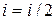 и переходят к символу 10.
и переходят к символу 10.
Если 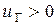 , то рассчитывают разность токов
, то рассчитывают разность токов 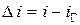 (символ 13) и определяют относительную погрешность разности токов через диод и через источник эдс (символ 14):
(символ 13) и определяют относительную погрешность разности токов через диод и через источник эдс (символ 14):  .
.
Если относительная погрешность больше требуемой, то вычисляют новое значение тока 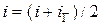 (символ 15) и переходят к символу 12.
(символ 15) и переходят к символу 12.
Если относительная погрешность меньше требуемой, то переходят к символу 16.
9. Определение промежуточных значений электрических величин (рис. 4.4, символ 16)
Рассчитывают:
1) 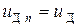 , 2)
, 2) 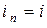 , 3)
, 3) 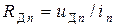 , 4)
, 4) 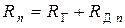 , 5)
, 5) 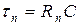 , 6)
, 6)  , 7)
, 7) 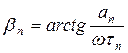 и переходят к символу 5.
и переходят к символу 5.
10. Определение промежуточных значений электрических величин (рис. 4.4, символ 19)
Рассчитывают выходное напряжение 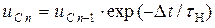 , пренебрегая обратным током диода, и переходят к символу 5.
, пренебрегая обратным током диода, и переходят к символу 5.
11. Вывод полученных результатов (рис. 4.4, символы 20, 21 и 22)
Вывод полученных результатов в виде таблиц и графиков является стандартной операцией и отдельного рассмотрения не требует.
|
|
|


