Расчёт параметрического стабилизатора на стабилитроне

ЛЕКЦИЯ 5

 

Стабилитроны и параметрические стабилизаторы напряжений

 

План лекции:

5.1. Пробой p-n -перехода

Стабилитроны

Расчёт параметрического стабилизатора на стабилитроне

Пробой p-n-перехода

Стабилитроном называют полупроводниковый диод, на обратной ветви которого имеется участок с сильной зависимостью тока от напряжения. Такая зависимость, как правило, обусловлена электрическим пробоем p-n-перехода.

Пробоем называют резкое увеличение обратного тока p-n-перехода при некотором обратном напряжении, превышающем напряжение пробоя . Различают электрический и тепловой пробои. Существуют три основных вида электрического пробоя: лавинный, туннельный и поверхностный.

Лавинный пробой вызывается ударной ионизацией нейтральных атомов кристаллической решётки полупроводника в обеднённом слое под действием сильного электрического поля. При обратном напряжении ток в p-n-переходе создаётся дрейфовым движением неосновных носителей заряда, приходящих из нейтральных p и n-областей. В обеднённом слое эти носители ускоряются и при напряжении, превышающем некоторое критическое значение, приобретают на длине свободного пробега кинетическую энергию, достаточную для того, чтобы при соударении с нейтральным атомом полупроводника произвести его ионизацию, т.е. создать новую пару носителей заряда – электрон и дырку. Вновь образовавшиеся носители будут ускоряться полем и могут также вызвать ионизацию. При этом может начинаться и начинается лавинообразный процесс роста количества носителей заряда. Соответственно нарастает обратный ток p-n-пере­хода.

Для оценки этого процесса введён коэффициент лавинного умножения , показывающий, во сколько раз обратный ток превышает исходную величину обратного теплового тока:

Коэффициент находят из эмпирической формулы

где параметр, зависящий от материала полупроводника и типа электропроводности базовой области, причём , напряжение лавинного пробоя, причём − обратное приложенное напряжение.

Для кремния n-типа и германия p-типа , а для кремния p-типа и германия n-типа . Зависимости обратного тока от обратного напряжения для двух значений приведены на рис. 5.1.

Рис. 5.1. Обратная ветвь вольтамперной характеристики p-n-перехода при лавинном пробое

Характерной особенностью лавинного пробоя является то, что с увеличением температуры напряжение пробоя 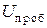возрастает. Следовательно, напряжение лавинного пробоя имеет положительный температурный коэффициент. Рост 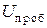при увеличении температуры происходит потому, что уменьшается длина свободного пробега носителей и для сообщения носителям заряда необходимой энергии требуется бóльшая напряжённость электрического поля.

Туннельный пробой представляет собой переход электронов сквозь потенциальный (энергетический) барьер между переходом - без изменения энергии. Такой переход называют туннельным эффектом.

Туннельный пробой возникает при очень высокой ( В/см) напряжённости электрического поля в обеднённом слое. Поэтому туннельный эффект наблюдается в узких переходах при толщине барьера порядка 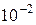мкм и с очень высокой концентрацией примеси () в переходах - . Напряжение туннельного пробоя составляет 0 ÷ 5 В.

В отличие от лавинного пробоя повышение температуры приводит к понижению напряжения туннельного пробоя из-за уменьшения ширины запрещённой зоны , т.е. из-за уменьшения высоты барьера. Следовательно, напряжение туннельного пробоя имеет отрицательный температурный коэффициент.

Установлено, что при , т.е. при невысоких концентрациях примеси, напряжение лавинного пробоя ниже, чем напряжение туннельного пробоя. При этом (> 6,6 В для Si), а при высоких концентрациях примеси () − выше, т.е. . При промежуточных концентрациях примеси, когда , пробой может объясняться обоими механизмами. Механизм пробоя в этом случае можно определить по знаку температурного коэффициента напряжения пробоя.

Крутизна вольтамперной характеристики при лавинном пробое больше, чем при туннельном, и поэтому дифференциальное сопротивление стабилитрона в зоне пробоя при лавинном пробое меньше, чем при туннельном. В силу этого эффект стабилизации при лавинном пробое более сильный, чем при туннельном.

Формула для расчёта напряжения пробоя при туннельном пробое в литературе отсутствует.

Поверхностный пробой объясняется резким увеличением тока утечки. Вследствие возможного загрязнения и наличия поверхностных зарядов между выходящими на поверхность участками p-n-перехода могут образовываться проводящие плёнки и каналы, по которым будет протекать ток утечки . Поверхностный пробой пропорционален величине обратного напряжения и в некоторых случаях может превысить тепловой ток, что эквивалентно пробою. Для уменьшения тока утечки принимают специальные конструкторские и технологические меры. Поэтому поверхностный пробой является крайне редким явлением.

Тепловой пробой обусловлен выделяющейся мощностью из-за протекания обратного тока под действием обратного напряжения

что вызывает разогрев p-n-перехода и прилегающих к нему областей полупроводника. Повышение температуры приводит к увеличению обратного тока и этот процесс может разрушить стабилитрон.

Выделяющаяся мощность за счёт теплопроводности отводится от зоны нагрева и рассеивается в окружающей среде. Кроме того, часть выделяющейся мощности отводится путём непосредственного излучения, однако этот механизм в данном случае является второстепенным.

Отводимая за счёт теплопроводности мощность пропорциональна разности температур перехода и окружающей среды и обратно пропорциональна тепловому сопротивлению участка конструкции p-n-переход − окружающая среда

Если скорость отвода мощности больше, чем скорость выделяющейся мощности, то может установиться тепловое равновесие, когда выполняется условие

которое определяет установившуюся (стационарную) температуру p-n-пере­хода.

Тепловой пробой не может быть использован в качестве механизма стабилизации. Он только ограничивает рабочую величину обратного тока лавинного или туннельного пробоя.

В p-n-переходах с большими обратными токами, например, в германиевых, тепловой пробой уже при комнатных температурах может наступать раньше, чем лавинный пробой. В кремниевых p-n-переходах обратные токи малы, так что раньше наступает лавинный пробой, диод может работать как стабилитрон. При высоких температурах тепловой пробой в кремниевых p-n-переходах может наступать раньше лавинного.

 

Стабилитроны

Стабилитроны применяют для стабилизации постоянного напряжения, имеющего пульсации и медленные изменения своей величины.

Различают стабилитроны общего назначения, прецизионные, импульсные, двуханодные и стабисторы.

Промышленность выпускает стабилитроны

− с напряжением стабилизации от 1,5 до 180 В,

− с токами стабилизации 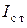от 0,5 мА до 1,4 А,

− с температурными коэффициентами напряжения стабилизации от 0,05 до 0,15 %/К, а для прецизионных стабилитронов с до 0,0005 %/К,

− с динамическим сопротивлением от долей и единиц Ома у мощных стабилитронов, до сотен и даже тысяч Ом у высоковольтных маломощных стабилитронов.

Двуханодные стабилитроны представляют собой встречно включенные p-n-переходы и предназначены для стабилизации разнополярных напряжений.

Стабистором называют полупроводниковый диод, у которого участок с сильной зависимостью тока от напряжения находится на прямой ветви ВАХ. Стабисторы предназначены как для стабилизации малых напряжений, так и для температурной компенсации схем.

Параметрами стабилитронов являются:

− − напряжение стабилизации стабилитрона – значение напряжения стабилитрона при протекании номинального тока стабилизации,

− − разброс номинального значения напряжения стабилизации,

− − минимальное напряжение стабилизации,

− − максимальное напряжение стабилизации,

− − изменение напряжения стабилизации при изменении тока стабилитрона относительно своего значения в рабочей точке,

− − ток стабилизации – значение постоянного тока, протекающего через стабилитрон в режиме стабилизации (ток, который рекомендуется в качестве номинального тока в схеме стабилизации и при котором определены остальные параметры стабилитрона),

− − минимальный ток стабилизации, обеспечивающий необходимую величину дифференциального сопротивления стабилитрона,

− − максимальный ток стабилизации, определяющий максимально допустимую величину отводимой (рассеиваемой) мощности,

− − дифференциальное сопротивление при номинальном токе стабилизации,

− − статическое сопротивление при номинальном токе стабилизации,

− − обратный ток стабилитрона при указанном обратном напряжении и др.

 

Расчёт параметрического стабилизатора на стабилитроне

Простейшая схема параметрического стабилизатора напряжения приведена на рис. 5.2.

 

Рис. 5.2. Простейшая схема стабилизатора напряжения

 

Данную схему стабилизатора напряжения называют параметрической потому, что стабилизация осуществляется за счёт изменения рабочих параметров стабилитрона.

Стабилитрон в схеме включают в обратном направлении относительно полярности входного напряжения, так как рабочей является обратная ветвь ВАХ стабилитрона. Сопротивление нагрузки включают параллельно стабилитрону. Сопротивление называют гасящим, так как на нём падает ("гасится") изменение входного напряжения. Кроме того, определяет качество стабилизации, которое оценивают с помощью коэффициента стабилизации

где − изменение входного напряжения относительно среднего (номинального), − соответствующее изменение напряжения стабилизации.

Исходными данными для расчёта стабилизатора постоянного напряжения являются:

1) напряжение и коэффициент стабилизации ,

2) сопротивление нагрузки ,

3) относительные интервалы изменения входного напряжения , напряжения стабилизации 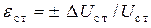,сопротивления нагрузки и гасящего сопротивления , причём , , , ,

4) исходная температура окружающей среды и интервал рабочих температур ÷ .

Постановка задачи: 1) подобрать тип стабилитрона, 2) рассчитать величину , токи и напряжения в рабочей точке и 3) обеспечить напряжение и коэффициент стабилизации 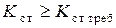в заданном интервале температур ÷ .

Алгоритм решения задачи.

1. Находят ток в нагрузке

2. Выбирают тип стабилитрона по условиям и .

3. Вольтамперную характеристику стабилитрона на участке стабилизации аппроксимируют прямой, проходящей через точку номинальных значений тока и напряжения стабилитрона (рис. 5.2)

где .

 

Рис. 5.2. Вольтамперная характеристика параметрического стабилизатора

 

4. Рассчитывают гасящее сопротивление .

Для этого вначале находят .

По второму закону Кирхгофа для схемы (рис. 5.1) составляют 2 уравнения:

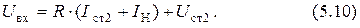
Подставляя в формулу уравнения (5.7) и (5.8), последовательно получаем

Так как , то получаем зависимость коэффициента стабилизации от параметров схемы, в том числе от величины гасящего сопротивления

Так как значение задано, то можно рассчитать величину гасящего сопротивления

Затем выбирают ближайшее большее значение из ряда номинальных величин сопротивлений.

5. Находят величину входного напряжения, используя уравнение

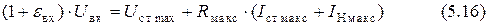
для случая, когда стабилитрон имеет максимальное напряжение стабилизации и оба тока максимальны. Здесь .

Если входное напряжение велико, например, , то на гасящем сопротивлении будет выделяться большая мощность. В этом случае более целесообразно использовать два последовательно включённых стабилизатора с коэффициентами стабилизации , причём напряжение стабилизации первого каскада должно быть больше, чем у второго.

6. Определяют напряжение в рабочей точке для найденного входного напряжения, используя уравнение (5.12)

7. Определяют ток стабилитрона в рабочей точке по формуле (5.8).

8. Вычисляют напряжение стабилизации и минимальный ток стабилитрона при минимальном входном напряжении, максимальном гасящем сопротивлении и минимальном сопротивлении нагрузки по формулам (5.17) и (5.8).

9. Вычисляют напряжение стабилизации 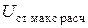и максимальный ток стабилитрона при минимальном входном напряжении, максимальном гасящем сопротивлении и минимальном сопротивлении нагрузки по формулам (5.17) и (5.8).

10. Проверяют пригодность выбранного стабилитрона найденным предельным величинам тока

Если оба условия выполняются, то стабилитрон выбран правильно и можно перейти к следующему шагу алгоритма.

В противном случае необходимо выбрать стабилитрон большей мощности и повторить действия, начиная с п.2.

11. Проверяют возможность превышения максимально допустимого тока в случае, когда и весь ток потечёт через стабилитрон. Из уравнения

Для наихудшего случая, когда , и получаем формулу

Если выполняется условие , то находят новое значение гасящего сопротивления по формуле

выбирают ближайшее большее значение из ряда номинальных величин сопротивлений и повторяют вычисления, начиная с п.5.

В противном случае переходят к следующему пункту алгоритма.

14. Рассчитывают величины и для всех сочетаний отклонений , и при минимальной и максимальной температурах.

15. Делают вывод о допустимых пределах изменения и области применения рассчитанного стабилизатора.

Поделиться:

Воспользуйтесь поиском по сайту: