 |
Корпускулярно-волновой дуализм
|
|
|
|
ЗАДАНИЕ № 29
Два источника излучают свет с длиной волны 375 и 750 нм. Отношение импульсов фотонов, излучаемых первым и вторым источником равно …
ВАРИАНТЫ ОТВЕТОВ:
1)  ; 2)
; 2)  ; 3) 2; 4) 4.
; 3) 2; 4) 4.
ЗАДАНИЕ № 30
Если скорость частиц одинакова, то наименьшей длиной волны обладает …
ВАРИАНТЫ ОТВЕТОВ:
1)  -частица; 2) нейтрон; 3) электрон; 4) протон.
-частица; 2) нейтрон; 3) электрон; 4) протон.
ЗАДАНИЕ № 31
Если частицы имеют одинаковую длину волны де Бройля, то наименьшей скоростью обладает …
ВАРИАНТЫ ОТВЕТОВ:
1)  -частица; 2) нейтрон; 3) позитрон; 4) протон.
-частица; 2) нейтрон; 3) позитрон; 4) протон.
ЗАДАНИЕ № 32
Если частицы имеют одинаковую скорость, то наибольшей длиной волны де Бройля обладает …
ВАРИАНТЫ ОТВЕТОВ:
1) электрон; 2) нейтрон; 3) протон; 4)  -частица.
-частица.
ЗАДАНИЕ № 33
Отношение длин волн де Бройля электрона и протона  , имеющих одинаковую скорость, составляет величину порядка…
, имеющих одинаковую скорость, составляет величину порядка…
ВАРИАНТЫ ОТВЕТОВ:
1)103; 2) 1; 3) 10;4)10–3 .
---------------------------
Указание к заданиям № 29 – 33
Связь между длиной волны де Бройля ( ) и импульсом (p) частицы:
) и импульсом (p) частицы:
 (h – постоянная Планка).
(h – постоянная Планка).
Для нерелятивистской частицы (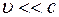 ) справедливо:
) справедливо:  ,
,
где m – масса частицы, а  – её скорость.
– её скорость.
ПОСТУЛАТЫ БОРА. СПЕКТР АТОМА ВОДОРОДА
ЗАДАНИЕ № 34
Электрон в атоме водорода перешёл из основного состояния в возбужденное с n=3. Радиус его боровской орбиты …
ВАРИАНТЫ ОТВЕТОВ:
1) увеличился в 2 раза;
2) увеличился в 3 раза;
3) увеличился в 9 раз;
4) уменьшился в 3 раза;
5) не изменился.
ЗАДАНИЕ № 35
Схемаэнергетических уровней атома водорода показана на рисунке …
ВАРИАНТЫ ОТВЕТА:


 1) 2) 3)
1) 2) 3)
ЗАДАНИЕ № 36
На рисунке представлена диаграмма энергетических уровней атома. Переход с поглощением фотона наибольшей частоты обозначен цифрой …
|
|
|
 |
ВАРИАНТЫ ОТВЕТА:
1) 1; 2) 2; 3) 3; 4) 4; 5) 5.
ЗАДАНИЕ № 37
Видимой части спектра излучения атома водорода соответствует формула …
ВАРИАНТЫ ОТВЕТА:
1)  , n = 2, 3, 4 …
, n = 2, 3, 4 …
2)  , n = 3, 4, 5 …
, n = 3, 4, 5 …
3)  , n = 4, 5, 6 …
, n = 4, 5, 6 …
4)  , n = 5, 6, 7 …
, n = 5, 6, 7 …
ЗАДАНИЕ № 38
На рисунке изображены стационарные орбиты атома водорода согласно модели Бора, а также условно изображены переходы электронов с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультра фиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, и инфракрасной – серию Пашена.
Наименьшей частоте кванта в серии Бальмера соответствует переход …
 |
ВАРИАНТЫ ОТВЕТОВ:
1) n = 2 → n = 1
2) n = 3 → n = 2
3) n = 4 → n = 3
4) n = 5 → n = 2
ЗАДАНИЕ № 39
На рисунке изображены стационарные орбиты атома водорода согласно модели Бора, а также условно изображены переходы электронов с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультра фиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, и инфракрасной – серию Пашена.
Наименьшей частоте кванта в серии Лаймана соответствует переход …
 |
ВАРИАНТЫ ОТВЕТОВ:
1) n = 5 → n = 1
2) n = 5 → n = 2
3) n = 5 → n = 3
ЗАДАНИЕ № 40
На рисунке изображены стационарные орбиты атома водорода согласно модели Бора, а также условно изображены переходы электронов с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультра фиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, и инфракрасной – серию Пашена.
Наименьшей частоте кванта в серии Пашена соответствует переход …

ВАРИАНТЫ ОТВЕТОВ:
1) n = 2 → n = 1
2) n = 4 → n = 3
3) n = 5 → n = 1
4) n = 5 → n = 3
ЗАДАНИЕ № 41
В атоме водорода электрон переходит с одного энергетического уровня на другой, как показано на рисунке.
|
|
|
Чему равно изменение его главного D n и орбитального D l квантовых чисел?
 |
ВАРИАНТЫ ОТВЕТОВ:
1) Δ n = –2; Δ l = +1
2) Δ n = +2; Δ l = –1
3) Δ n = –1; Δ l = 0
4) Δ n = +1; Δ l = +1
5) Δ n = +2; Δ l = +1
ЗАДАНИЕ № 42
В атоме водорода электрон переходит с одного энергетического уровня на другой, как показано на рисунке.
Чему равно изменение его главного D n и орбитального D l квантовых чисел?
 |
ВАРИАНТЫ ОТВЕТОВ:
1) Δ n = +2; Δ l = –1
2) Δ n = +2; Δ l = +1
3) Δ n = –2; Δ l = +1
4) Δ n = –1; Δ l = 0
5) Δ n = –2; Δ l = –1
ЗАДАНИЕ № 43
При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определённые ограничения (правила отбора). В энергетическом спектре атома водорода запрещённым переходом является …
ВАРИАНТЫ ОТВЕТОВ:
1) 4f – 3d; 2) 4s – 3p; 3) 3s – 2s; 4) 3p – 2s.
ЗАДАНИЕ № 44
При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определённые ограничения (правила отбора).
 |
Если система энергетических уровней атома водорода имеет вид, представленный на рисунке, то запрещёнными переходами являются …
А) 5p-2s; B) 3s-2s; C) 4s-3p; D) 4f-3p.
ВАРИАНТЫ ОТВЕТОВ:
1) A, C; 2) B, C; 3) A, D; 4) B, D.
ЗАДАНИЕ № 45
Закон сохранения момента импульса накладывает ограничения на возможные переходы электрона в атоме водорода с одного уровня на другой (правила отбора). В энергетическом спектре атома водорода (рисунок) запрещённым переходом является …
ВАРИАНТЫ ОТВЕТОВ:
 1) 3s – 2p
1) 3s – 2p
2) 4s – 3p
3) 4s – 3d
4) 2p – 1s
---------------------------
Указание к заданиям № 34 - 45
ПОСТУЛАТЫ БОРА
Первый постулат. В атоме существуют стационарные (не изменяющиеся со временем) состояния, характеризующиеся определенными дискретными значениями энергии. Стационарным состояниям атома соответствуют стационарные op6иты, на которых находятся электроны. В соответствии с первым постулатом Бора электрон, двигаясь по круговой стационарной орбите обладает определенным значением момента импульса, удовлетворяющем условию:
 ,
,
где me –масса электрона,
υn – скорость электрона на n -й орбите радиуса rn,
|
|
|
ħ=h/2π (h – постоянная Планка).
Радиус n -ой орбиты для атома водорода:

где e – заряд электрона, ε о – электрическая постоянная.
По теории Бора полная энергия электрона в атоме водорода может принимать дискретный ряд значений:

где n – номер орбиты электрона (номер стационарного состояния атома).
Второй постулат. При переходе электрона с одной орбиты на другую излучается фотон с энергией hν, равной разности энергий соответствующих стационарных состояний En и Еm:
hν= En– Em.
Наборвозможных дискретных частот ν переходов атома между стационарными состояниями атома определяет линейчатый спектр атома.
В спектре атома водорода частота квантового перехода:
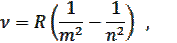
где R – постоянная Ридберга, m = 1, 2, 3, …; n = m +1, m +2, m +3, …
Эта обобщенная формула Бальмера описывает серии линий в спектре атома водорода, где m определяет серию (m = 1, 2, 3…), а n определяет отдельные линии соответствующей серии (n = m +1, m +2, …).
В ультрафиолетовой области спектра атома водорода наблюдается

В видимой области спектра атома водорода наблюдается

В инфракрасной области спектра атома водорода наблюдаются




В квантовой механике считается, что электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема. Размер, форму и ориентацию электронного облака в пространстве характеризуют, соответственно, квантовые числа n, l и ml.
n (главное квантовое число) определяет энергетические уровни электрона в атоме, принимая следующие значения: п = 1,2,3,...;
l (орбитальное квантовое число) определяет форму электронного облака, принимая следующие значения: l = 0, 1, 2,... n –1;
ml (магнитное квантовое число определяет ориентацию электронного облака в пространстве, принимая следующие значения: ml =0, ±1, ±2, …± l.
Состояние электрона в атоме водорода определяется набором квантовых чисел.
При l = 0 состояние электрона называется s -состоянием, при l= 1состояние электрона соответствует р -состоянию, при l = 2 – d -состоянию и т. д.
|
|
|
При записи состояния электрона значение n указывается перед условным обозначением орбитального квантового числа, например, 2s (n = 2, l = 0).
Правила, ограничивающие число возможных переходов электронов при испусканием или при поглощением света, называются правилами отбора.
Правила отбора для орбитального и магнитного квантовых чисел:
∆ l = ±1; ∆ ml = 0, ±1.
С учетом этих правил отбора спектральной серии Лаймана соответствуют переходы: np → 1 s (n = 2, 3, 4,...), а для серии Бальмера соответствуют переходы np → 2 s, ns → 2 p, nd → 2 p (n = 3, 4,...) и т. д.
УРАВНЕНИЕ ШРЕДИНГЕРА
УСЛОВИЕ К ЗАДАНИЯМ №№ 46-51
Ниже приведены несколько видов уравнения Шредингера для общего и частного случаев:
А )  ;
;
Б )  ;
;
В )  ;
;
Г )  ;
;
Д )  ;
;
E )  .
.
ЗАДАНИЕ № 46
Общим уравнением Шредингера является…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 47
Уравнением Шредингера для стационарных состояний в общем случае является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 48
Уравнением Шредингера для электрона в водородоподобном атоме является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 49
Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 50
Уравнением Шредингера для частицы в трехмерной прямоугольной «потенциальной яме» с бесконечными прямоугольными стенками является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 51
Уравнением Шредингера для частицы в одномерной прямоугольной «потенциальной яме» с бесконечными прямоугольными стенками является уравнение …
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Указание к заданиям № 46 – 51
Общее уравнение Шредингера:
 ,
,
где  – волновая функция;
– волновая функция;
 ;
;
m −масса частицы;
 (
(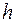 − постоянная Планка);
− постоянная Планка);
 − потенциальная энергия.
− потенциальная энергия.
Для стационарного случая уравнение Шредингера:
 или
или
 ,
,
где E – энергия частицы.
Для электрона в водородоподобном атоме функция потенциальной энергии  обладает центральной симметрией и задается выражением
обладает центральной симметрией и задается выражением  ,
,
где Z – число протонов в ядре (порядковый номер атома в таблице Менделеева);
Z e – заряд ядра (е – величина заряда электрона);
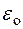 − электрическая постоянная;
− электрическая постоянная;
r – расстояние от ядра до точки (x, y, z).
Линейный гармонический осциллятор относится к одномерному случаю и потенциальная энергия задается выражением:
 ,
,
где m − масса частицы;
 − собственная циклическая частота осциллятора;
− собственная циклическая частота осциллятора;
|
|
|
 − координата частицы.
− координата частицы.
Для частиц в трехмерной или одномерной прямоугольной «потенциальной яме» с бесконечными прямоугольными стенками потенциальная энергия внутри «ямы» равна нулю ( = 0 или
= 0 или  ).
).
Волновая функция
ЗАДАНИЕ № 52
На рисунках приведены картины распределения плотности вероятности нахождения электрона в потенциальном ящике с бесконечно высокими стенками.

Какая из картин соответствует состоянию с квантовым числом n= 3?
ВАРИАНТЫ ОТВЕТОВ:
1) А; 2) Б; 3) В; 4) Г; 5) Ни одна из них.
ЗАДАНИЕ № 53
На рисунке приведен график волновой функции электрона в «потенциальной яме».

Вероятность нахождения электрона на отрезке  L < x <
L < x <  L равна...
L равна...
ВАРИАНТЫ ОТВЕТОВ:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
ЗАДАНИЕ № 54
Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле  , где w − плотность вероятности, определяемая
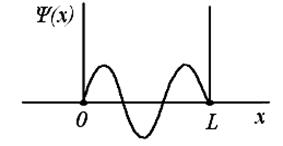
, где w − плотность вероятности, определяемая 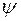 - функцией. Если
- функцией. Если  – функция имеет вид, указанный на рисунке, то вероятность обнаружить на участке
– функция имеет вид, указанный на рисунке, то вероятность обнаружить на участке 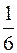 L < x <
L < x <  L равна:
L равна:

ВАРИАНТЫ ОТВЕТОВ:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) 1.
; 4) 1.
ЗАДАНИЕ № 55
На рисунке приведена картина распределения плотности вероятности нахождения электрона в потенциальном ящике с бесконечно высокими стенками. Вероятность обнаружить электрон на отрезке  равна...
равна...

| ВАРИАНТЫ ОТВЕТОВ:
1) 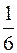 ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; 5) ; 5)  . .
|
_ _ _ _ _ __ _ _ _ _ _ _ _ __ _
Указание к заданиям № 51 -55
Для частицы, находящейся в одномерной «потенциальной яме» с бесконечными стенками и плоским дном волновая функция Ψn (х) имеет следующий вид:  , где L – ширина «потенциальной ямы»,
, где L – ширина «потенциальной ямы»,
n – главное квантовое число (номер квантового состояния), которое характеризует энергетический уровень. В этом случае плотность вероятности  будет иметь вид:
будет иметь вид:  ,
,
где знак * означает комплексное сопряжение.
На участке  волновая функция Ψn (х) имеет n экстремумов, а функция плотности вероятности
волновая функция Ψn (х) имеет n экстремумов, а функция плотности вероятности  имеет n максимумов.
имеет n максимумов.
Вероятность 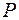 обнаружить электрон на участке (
обнаружить электрон на участке ( ) вычисляется по формуле:
) вычисляется по формуле: 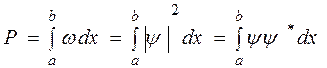 .
.
При этом вероятность  обнаружить электрон на всем участке L (
обнаружить электрон на всем участке L ( ,
,  ) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой
) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой 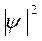 на всем участке L (
на всем участке L ( ,
,  ) равна единице, а вероятность обнаружить электрон на интервале (
) равна единице, а вероятность обнаружить электрон на интервале ( ) равна отношению площадей под кривой
) равна отношению площадей под кривой 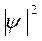 на этом интервале (
на этом интервале ( ) и на всем интервале (
) и на всем интервале ( ) для
) для  ,
,  .
.
|
|
|
12 |


