 |
Основные алгебраические операции с матрицами
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ КАЛУЖСКОЙ ОБЛАСТИ
ГБПОУ КО «Калужский торгово-экономический колледж»
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ
к контрольной работе
по дисциплине «МАТЕМАТИКА»
для студентов I курса заочного отделения
СОДЕРЖАНИЕ
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ.. 3
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ.. 5
ЗАДАНИЯ ДЛЯ СТУДЕНТОВ.. 9
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.. 14
ПРИЛОЖЕНИЯ.. 15
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа должна содержать:
1. Титульный лист
2. Рецензия
3. Оглавление
4. Содержание работы
Работа выполняется вручную
Контрольная работа может быть выполнена по усмотрению студента:
- либо в обычной ученической тетради,
- либо на листах формата А4.
Титульный лист. Заполняется по образцу.
Рецензия. Содержит один чистый лист для рецензии работы.
Оглавление. Содержит перечень заданий с указанием номеров страниц.
Содержание работы.
Каждый вариант контрольной работы содержит 6 заданий. Задания выполняются в указанном порядке. Условия заданий должны быть записаны полностью. Каждое задание начинается с новой страницы. В решении задач необходимо указать все используемые формулы; решение должно содержать комментарии или пояснения, указаны все расчеты и показаны все преобразования, выполняемые с алгебраическими выражениями.
После выполнения контрольная работа сдается на проверку.
Студент должен ознакомиться с результатами проверки работы. На экзамене (зачете) студент должен дать все необходимые пояснения по решенным заданиям. При затруднениях, возникших при выполнении контрольной работы, студент может получить консультацию преподавателя.
|
|
|
Номер варианта выбирается по последней цифре зачетной книжки.
| ЦИФРА | ВАРИАНТ | ЦИФРА | ВАРИАНТ |
| 1 вариант | 6 вариант | ||
| 2 вариант | 7 вариант | ||
| 3 вариант | 8 вариант | ||
| 4 вариант | 9 вариант | ||
| 5 вариант | 10 вариант |
Номера задач каждого варианта приведены в таблице:
| Вариант | Номера заданий | |||||
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Упражнение 1. Выполнить операции над матрицами.
Основные алгебраические операции с матрицами
Равенство двух матриц. Две матрицы считают равными, если эти матрицы имеют одинаковые размерности и равны все их соответствующие элементы.
Сложение двух матриц. Сложить можно только матрицы одинаковой размерности. Суммой матриц А и В называют матрицу С, элементы которой равны сумме соответствующих элементов складываемых матриц. Например,
Некоторые свойства сложения матриц
А + В = В + А; (А + В) + С = А +(В + С).
Умножение матрицы на число. Все элементы исходной матрицы умножаются на заданное число. Например,
Умножение матриц.
Две матрицы могут быть перемножены только тогда, когда число столбцов в первой матрицы равно числу строк во второй (такие матрицы называются согласованными).
То есть, если матрица А имеет размер [n,p], а матрица В - размер [p,m], то результирующая матрица будет иметь размер [n,m]
Символически это правило может быть выражено в следующем виде:
(n,p) х (p,m) = (n,m)
Для вычисления элементов результирующей матрицы существует следующее правило: элементы, стоящие в i-ой строке и j- ом столбце, равны сумме произведений элементов первой матрицы, стоящих в i-ой строке на элементы второй матрицы, стоящие в j- ом столбце.
|
|
|
Примеры умножения матриц произвольного порядка:
1) 
Данные матрицы перемножить невозможно, так как они не являются согласованными – количество столбцов в первой матрице равно 2, а количество строк во второй матрице равно 3.
2) 
Данные вычисления могут быть записаны и в таком виде
3) Выполним теперь умножение матриц В х А. Получаем
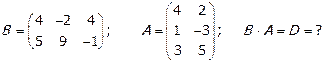
Очевидно, что размеры результирующей матрицы D - [2,2].
Из примеров 2 и 3 видно, что произведение матриц не коммутативно (в общем случае), т.е. 
.
Упражнение 2. Найти производные, пользуясь правилами и формулами дифференцирования (Приложение 1).
Решение:
Кроме формул дифференцирования нужно использовать правила дифференцирования (суммы, разности, произведения, частного).
Необходима и теорема о производной сложной функции:
если задана сложная функция 
, где 
, то есть 
; если каждая из функций 
и 
дифференцируема по своему аргументу, то
.
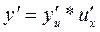1) 
, 
,
.
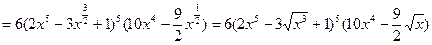2) 
,
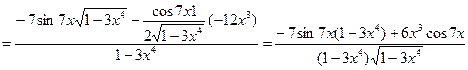
3) 
4) 
Упражнение 3. Исследовать функцию методами дифференциального исчисления и начертить график.
Исследование функции и построение графика рекомендуется проводить по следующей схеме:
1) найти область определения функции D(y);
2) найти точки экстремума функции и определить интервалы ее монотонности;
3) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции;
4) найти асимптоты графика функции;
5) построить график, используя результаты предыдущих исследований;
6) дополнительно найти наибольшее и наименьшее значения на отрезке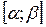 
.
Решение:
Дана функция: 
1) Областью определения данной функции являются все действительные значения аргумента х, то есть D(y): 
, а это значит, что функция непрерывна на всей числовой прямой и график ее не имеет вертикальных асимптот.
2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки I рода х1 = -5, х2 = -1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
|
|
|
| x | 
| -5 |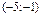 
| -1 | 
|
| + | - | + | ||
| & | max | ( | min | & |
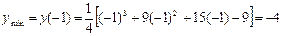
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем II производную заданной функции и приравняем ее к нулю:
, т.е. 
Итак, функция имеет одну критическую точку 2 рода 
. Разобьем область определения полученной точкой на части, в каждой из которой установим знак II производной:
| x | 
| -3 | 
|
| - | + | |
| 
| т.п. | 
|
Значение является абсциссой точки перегиба графика функции, а ордината этой точки 
4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты 
воспользуемся формулами: 
.
Имеем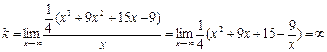 
.
Таким образом, у графика заданной функции наклонных асимптот нет.
5) 
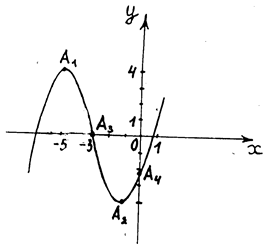Для построения графика в выбранной системе координат изобразим точки максимума А1(-5; 4), минимума А2(-1; -4), перегиба А3 (-3; 0) и точку пересечения графика с осью Оу А4 (0; 
С учетом результатов предыдущих исследований построим кривую.
6) Найдем наибольшее и наименьшее значения заданной функции на отрезке 
. Для этого посчитаем значения функции на концах этого отрезка, в критических точках I рода, попавших на отрезок, и сравним результаты:
.
Очевидно, что 
.
Упражнение 4. Задан закон s(t) изменения пути движения материальной точки; нужно найти значения скорости и ускорения этой точки в момент времени t0.
Решение:
Пусть 
.
Известно, что значения скорости и ускорения материальной точки в некоторый момент времени являются соответственно значениями в этот момент I и II производных функции, задающей закон изменения пути движения точки.
У нас 
(ед. ск.)
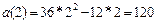(ед. уск.)
ЗАДАНИЯ ДЛЯ СТУДЕНТОВ
В заданих 1-10 найти матрицу С, выполнив операции над матрицами А и В:
№ 1.
С = А(2А + В), 
№2.
С = 2А(А + В), 
№3.
С = (А + 2В)А, 
.
№4.
С = 3В(А – В), 
№5.
С = 2А(В – А), 
№6.
С = А(2А + В),
№7.
С = 2А(А + В),
№8.
С = (А + 2В)А, .
№9.
С = 3В(А – В),
№10.
С = 2А(В – А),
|
|
|
В задачах 11-20 найти производные, пользуясь правилами и формулами дифференцирования:
№ 11
1) Найдите производную функции 
2) Найдите значение производной функции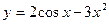 
в точке 
3) Найдите значение производной функции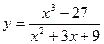 
в точке 
4) f(х) = (3х-2) 
. Найдите f ׳(1).
5) f(х) = 5 
Вычислите f ׳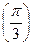 
6) Найдите значение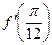 
, если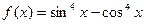 
7) Решите уравнение 
, если f(x) =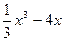 
; g(x) =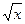 
№12
1) Найдите производную функции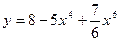 
2) Найдите значение производной функции 
в точке 
3) Найдите производную функции 
4) Найдите значение производной функции 
в точке 
5) f(х) = 3 
Вычислите f ׳ 
.
6) Найдите значение 
, если 
7) Решите уравнение , если f(x) = 
; g(x) = 2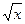
№13
1) Найдите производную функции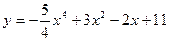 
2) Найдите значение производной функции 
в точке
3) Найдите значение производной функции 
в точке 
.
4) f(х) = (3х + 2) . Найдите f ׳(-1).
5) f(х) = 5 Вычислите f ׳ .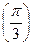
6) Найдите значение 
, если 
7) Решите уравнение , если f(x) = 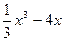; g(x) =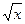
№14
1) Найдите производную функции 
2) Найдите значение производной функции 
в точке 
3) Найдите производную функции 
4) f(х) = (5х + 4) 
. Найдите f ׳(- 1).
5) f(х) = 3 Вычислите f ׳ 
.
6) Найдите значение , если
7) Решите уравнение , если f(x) = ; g(x) = 2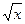
№ 15
1) Найдите производную функции
2) Найдите значение производной функции 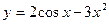в точке
3) Найдите значение производной функции 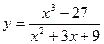в точке
4) f(х) = (3х-2) . Найдите f ׳(1).
5) f(х) = 5 Вычислите f ׳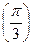
6) Найдите значение 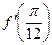, если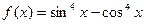
7) Решите уравнение , если f(x) = 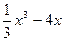; g(x) =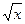
№16
1) Найдите производную функции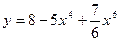
2) Найдите значение производной функции в точке
3) Найдите производную функции
4) Найдите значение производной функции в точке
5) f(х) = 3 Вычислите f ׳ .
6) Найдите значение , если
7) Решите уравнение , если f(x) = ; g(x) = 2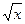
№17
1) Найдите производную функции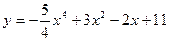
2) Найдите значение производной функции в точке
3) Найдите значение производной функции в точке .
4) f(х) = (3х + 2) . Найдите f ׳(-1).
5) f(х) = 5 Вычислите f ׳ .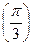
6) Найдите значение , если
7) Решите уравнение , если f(x) = 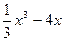; g(x) =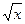
№18
1) Найдите производную функции
2) Найдите значение производной функции в точке
3) Найдите производную функции
4) f(х) = (5х + 4) . Найдите f ׳(- 1).
5) f(х) = 3 Вычислите f ׳ .
6) Найдите значение , если
7) Решите уравнение , если f(x) = ; g(x) = 2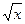
№ 19
1) Найдите производную функции
2) Найдите значение производной функции 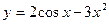в точке
3) Найдите значение производной функции 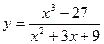в точке
4) f(х) = (3х-2) . Найдите f ׳(1).
5) f(х) = 5 Вычислите f ׳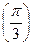
6) Найдите значение 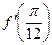, если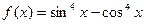
7) Решите уравнение , если f(x) = 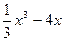; g(x) =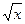
№20
1) Найдите производную функции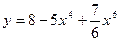
2) Найдите значение производной функции в точке
3) Найдите производную функции
4) Найдите значение производной функции в точке
5) f(х) = 3 Вычислите f ׳ .
|
|
|
6) Найдите значение , если
7) Решите уравнение , если f(x) = ; g(x) = 2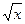
В задачах 21-30 исследовать функцию методами дифференциального исчисления и начертить график:
№ 21
№ 22
№ 23
№ 24
№ 25
№ 26
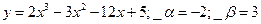
№ 27
№ 28
№ 29
№ 30
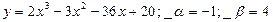
В задачах 31-40 задан закон s(t) изменения пути движения материальной точки; нужно найти значения скорости и ускорения этой точки в момент времени t0:
№ 31
№ 32
№ 33
№ 34
№ 35
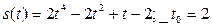
№36
№ 37
№ 38
№ 39
№ 40
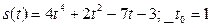
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Богомолов Н.В. Математика: учеб. для ссузов. - М.: Дрофа, 2012. - 400 с.
2. Богомолов Н.В. Практические занятия по математике. - М.: Высш. шк., 2012. - 495 с.
3. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2014. - 208 с.
4. Валуцэ И.И. Математика для техникумов. – М.: Наука. Гл. ред. Физ.мат. лит., 2013 – 576 с.: ил.
5. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2. - М.: ООО "Издательство Оникс", 2012. - 416 с.
6. Кремер Н.Ш. Высшая математика для экономистов - М.: ЮНИТИ, 2013. - 471 с.
7. Кремер Н.Ш. Высшая математика для экономистов. Практикум - М.: ЮНИТИ, 2013. - 479 с.
8. Кремер Н.Ш. «Теория вероятностей и математическая статистика», учебник, ЮНИТИ-ДАТА, 2010. 551 с.
9. Пехлецкий И.Д. Математика. - М.: Издательский центр "Академия", 2014. - 320 с.
10. Соловейчик И.Л. Сборник задач по математике с решениями для техникумов. - М.: ООО "Издательский дом "ОНИКС 21 век", 2014. - 464 с.
ПРИЛОЖЕНИЯ
Приложение 1
Формулы дифференцирования
| Правила дифференцирования
|
Таблица значений тригонометрических функций
|
|
|
|
