Тема 2.1. Основные положения, метод

Метод сечений

Метод сечений заключается в мысленном рассечении тела плоскостью и рассмотрении равновесия любой из отсеченных ча­стей.

Если все тело находится в равновесии, то и каждая его часть находится в равновесии под действием внешних и внутренних сил. Внутренние силы определяются из уравнений равновесия, соста­вленных для рассматриваемой части тела.

Рассекаем тело поперек плоскостью (рис. 19.1). Рассматрива­ем правую часть. На нее действуют внешние силы F 4; F 5; F 6 и внутренние силы

Тема 2.1. Основные положения 169

упругости qk, распределенные по сечению. Систему распределенных сил можно заменить главным вектором Rq, поме­щенным в центр тяжести сечения, и суммарным моментом сил Mo^:

n

Разложив главный вектор R о по осям, получим три составляющие:

где N_z — продольная сила;

Q_x — поперечная сила по оси х;

Q_y — поперечная сила по оси у.

Главный момент тоже принято представлять в виде моментов пар сил в трех плоскостях проекции:

М₀ = М_х + М_у + М_z,

М_х — момент сил относительно Ох; М_у — момент сил относитель­но Оу; M_z — момент сил относительно Oz.

Полученные составляющие сил упругости носят название вну­тренних силовых факторов. Каждый из внутренних силовых фак­торов вызывает определенную деформацию детали. Внутренние си­ловые факторы уравновешивают приложенные к этому элементу де­тали внешние силы. Используя шесть уравнений равновесия, можно получить величину внутренних силовых факторов:

170 Лекция 19

 

Из приведенных уравнений следует, что:

N_z — продольная сила, равная алгебраической сумме проекций на ось Oz внешних сил, действующих на отсеченную часть бруса; вызывает растяжение или сжатие;

Q_x — поперечная сила, равная алгебраической сумме проекций на ось Qx внешних сил, действующих на отсеченную часть;

Q_y — поперечная сила, равная алгебраической сумме проекций на ось Оу внешних сил, действующих на отсеченную часть;

силы Q_x и Q_y вызывают сдвиг сечения;

М_г — крутящийся момент, равный алгебраической сумме мо­ментов внешних сил относительно продольной оси Oz; вызывает скручивание бруса;

М_х — изгибающий момент, равный алгебраической сумме мо­ментов внешних сил относительно оси Ох;

М_у — изгибающий момент, равный алгебраической сумме мо­ментов внешних сил относительно оси Оу;

моменты М_х и М_у вызывают изгиб бруса в соответствующей плоскости.

Напряжения

Метод сечений позволяет определить величину внутреннего си­лового фактора в сечении, но не дает возможности установить за­кон распределения внутренних сил по сечению. Для оценки прочно­сти необходимо определить величину силы, приходящуюся на любую точку поперечного сечения.

Величину интенсивности внутренних сил в точке поперечного сечения называют механическим напряжением. Напряжение харак­теризует величину внутренней силы, приходящейся на единицу пло­щади поперечного сечения.

Тема 2.1. Основные положения 171

Рассмотрим брус, к которому приложена внешняя нагрузка (рис. 19.2). С помощью метода сечений рассечем брус поперечной плоскостью, отбросим левую часть и рассмотрим равновесие остав­шейся правой части. Выделим на секущей плоскости малую площадку ΔА На этой площадке действует равнодействующая внутренних сил упругости. Направление напряжения р_ср совпадает с направлением внутренней силы в этом сече­нии.

Вектор р_ср называют полным напряжени­ем. Его принято раскладывать на два вектора (рис. 19.3): τ — лежащий в площадке сечения и σ — направленный перпендикулярно площад­ке.

Если вектор р — пространственный, то его раскладывают на три составляющие:

Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию.

Касательное напряжение характеризует сопротивление сечения сдвигу.

Сила N (продольная) вызывает появление нормального напря­жения а. Силы Q_x и Q_y вызывают появление касательных напря­жений т. Моменты изгибающие М_х и М_у вызывают появление нор­мальных напряжений ст, переменных по сечению.

Крутящий момент M_z вызывает сдвиг сечения вокруг продоль­ной оси, поэтому появляются касательные напряжения т.

Примеры решения задач

Пример 1. Определить величину продольной силы в сечении 1-1 (рис. 19.4).

Решение

172 Лекция 19

 

Рассматривая левую часть бруса, определяем N_z1= -12 + 8 - 5 = 9кН. Рассматривая правую часть бруса, определяем N_z1=23 — 14 = 9кН.

 

Величина продольной силы в сечении не зависит от того, какая часть бруса рассматривается.

Пример 2. Определить внутренний силовой фактор в сечении 1-1 (рис. 19.5а).

Решение

Контрольные вопросы и задания

1. Какие силы в сопротивлении материалов считают внешними?
Какие силы являются внутренними?

2. Какими методами определяют внешние силы? Как называют
метод для определения внутренних сил?

3. Сформулируйте метод сечений.

Тема 2.1. Основные положения 173

4. Как в сопротивлении материалов располагают систему коор­динат?

5. Что в сопротивлении материалов называют внутренними си­ловыми факторами? Сколько в общем случае может возникнуть вну­тренних силовых факторов?

6. Запишите систему уравнений, используемую при определении внутренних силовых факторов в сечении?

7. Как обозначается и как определяется продольная сила в сече­нии?

8. Как обозначаются и как определяются поперечные силы?

9. Как обозначаются и определяются изгибающие и крутящий моменты?

10. Какие деформации вызываются каждым из внутренних си­ловых факторов?

11. Что называют механическим напряжением?

12. Как по отношению к площадке направлены нормальное и касательные напряжения? Как они обозначаются?

13. Какие напряжения возникают в поперечном сечении при дей­ствии продольных сил?

14. Какие напряжения возникают при действии поперечных сил?

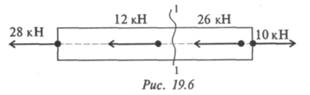
15. С помощью метода сечений определите величину внутрен­него силового фактора в сечении 1-1 и вид нагружения (рис. 19.6).

 

16. С помощью метода сечений определите величину момента
m4, величину внутреннего силового фактора в сечении 2-2 и вид
нагружения (рис. 19.7).

174 Лекция 19

17. Ответьте на вопросы тестового задания.

Тема 2.1. Основные положения, метод

Сечений, напряжения

 

Тема 2.1. Основные положения 175

 

 

Поделиться:

Воспользуйтесь поиском по сайту: