Основы динамики системы материальных точек

Тема 1.15. Общие теоремы динамики

Иметь представление о понятиях «импульс силы», «количе­ство движения», «кинетическая энергия»; о системе материаль­ных точек, о внутренних и внешних силах системы.

Знать основные теоремы динамики, основные уравнения дина­мики при поступательном и вращательном движениях твердого тела, формулы для расчета моментов инерции некоторых одно­родных твердых тел.

Уметь определять параметры движения с помощью теорем динамики.

Теорема об изменении количества движения

Количеством движения материальной точки называется век­торная величина, равная произведению массы точки на ее скорость mv.

Вектор количества движения совпадает по направлению с век­тором скорости. Единица измерения [mv] — кг∙м/с.

Произведение постоянного вектора силы на некоторый проме­жуток времени, в течение которого действует эта сила, называется импульсом силы Ft.

Вектор импульса силы по направлению совпадает с вектором силы.

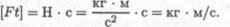
Использовав основное уравнение динамики, после преобразова­ния можно получить соотношение между количеством движения и импульсом силы (рис. 17.1).

122 Лекция 17

Полученное соотношение выражает теорему об изменении коли­чества движения точки:

Изменение количества движения точки за некоторый проме­жуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени.

Теорема об изменении кинетической энергии

Энергией называется способность тела совершать механиче­скую работу.

Существуют две формы механической энергии: потенциальная энергия, или энергия положения, и кинетическая энергия, или энергия движения.

Потенциальная энергия (П) определяет способность тела совер­шать работу при опускании с некоторой высоты до уровня моря. Потенциальная энергия численно равна работе силы тяжести.

П = Gh, где h — высота точки над уровнем моря.

Кинетическая энергия (К) определяется способностью движу­щегося тела совершать работу. Для материальной точки кинетиче­ская энергия рассчитывается по формуле

Кинетическая энергия — величина скалярная, положительная.

Единицы измерения:

Энергия имеет размерность работы.

Запишем для материальной точки (рис. 17.2) основное уравнение движения

Спроектируем обе части векторного равенства на направление скорости:

Тема 1.15. Общие теоремы динамики 123

Умножив обе части полученного выражения на некоторое пере­мещение dS, получим:

Полученное равенство выражает теорему об изменении кинети­ческой энергии точки:

Изменение кинетической энергии на некотором пути равно ра­боте всех действующих на точку сил на том же пути.

Основы динамики системы материальных точек

Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.

Любое материальное тело в механике рассматривается как меха­ническая система, образуемая совокупностью материальных точек.

Из определения механической системы следует, что движение каждой из точек, входящих в систему, зависит от движения осталь­ных точек.

Силы, действующие на точки системы, делятся на внешние и внутренние. Силы взаимодействия между точками этой системы называют внутренними. К внешним силам относятся силы, действу­ющие со стороны точек, не входящих в эту систему.

Примерами внешних сил являются сила тяжести, сила давле­ния, сила трения и др.

К внутренним силам относятся силы упругости.

Движение механической системы зависит не только от внешних сил, но и от

n

суммарной массы системы m = ∑ Δ m k, где Δ m k -- масса отдельных точек

механической системы.

 

124 Лекция 17

Движение системы зависит и от положения центра масс си­стемы — условной точки, в которой сосредоточена вся масса тела. Обычно считают, что в центре масс приложены все внешние силы.

Движение центра масс определяет движение всей системы толь­ко при поступательном движении, при котором все точки тела дви­жутся одинаково.

12	Поделиться:

Воспользуйтесь поиском по сайту: