Виды расчетов на прочность

Тема 2.5. Кручение.

Напряжения и деформации

При кручении

Иметь представление о напряжении и деформациях при круче­нии, о моменте сопротивления при кручении.

Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.

Напряжения при кручении

Проводим на поверхности бру­са сетку из продольных и попе­речных линий и рассмотрим рису­нок, образовавшийся на поверхно­сти после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол φ, продольные линии искривляют­ся, прямоугольники превращают­ся в параллелограммы. Рассмотрим элемент бруса 1234 после деформа­ции.

При выводе формул используем закон Гука при сдвиге и гипотезу

224 Лекция 27

плоских сечений и неискривления радиусов поперечных сечений.

При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.16).

При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1г).

Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

Закон Гука при сдвиге τ = Gγ,

G — модуль упругости при сдвиге, Н/мм²; γ -- угол сдвига, рад.

Напряжение в любой точке поперечного сечения

Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости d Q (рис. 27.2).

где τ — касательное напряжение; dA — элементарная площадка.

В силу симметрии сечения силы dQ образуют пары (см. лекцию 26).

Элементарный момент силы dQ относительно центра круга

где р — расстояние от точки до центра круга.

Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов:

После преобразования получим формулу для определения напря­жений в точке поперечного сечения:

Тема 2.5. Кручение 225

При ρ = 0 τ_к = 0; касательное напряжение при кручении про­порционально расстоянию от точки до центра сечения. Полученный интеграл J_p (лекция 25) называется полярным моментом инерции сечения. J_p является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию.

Анализ полученной формулы для J_p показывает, что слои, рас­положенные дальше от центра, испытывают большие напряжения.

Эпюра распределения касательных напряжений при кручении (рис. 27.3)

Максимальные напряжения при кручении

Из формулы для определения напряжений и эпюры распределе­ния касательных напряжений при кручении видно, что максималь­ные напряжения возникают на поверхности.

Определим максимальное напряжение, учитывая, что р_тaх = d/2, где d — диаметр бруса круглого сечения.

Для круглого сечения полярный момент инерции рассчитыва­ется по формуле (см. лекцию 25).

Максимальное напряжение возникает на поверхности, поэтому имеем

Обычно Jp/ р_тaх обозначают W_p и называют моментом сопро­тивления при кручении, или полярным моментом сопротивления сечения

8 - 8060 Олофинская

226 Лекция 27

Таким образом, для расчета максимального напряжения на по­верхности круглого бруса получаем формулу

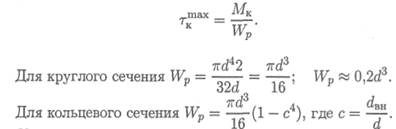
Условие прочности при кручении

Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности

где [τ_к] — допускаемое напряжение кручения.

Виды расчетов на прочность

Существует два вида расчета на прочность

1. Проектировочный расчет — определяется диаметр бруса
(вала) в опасном сечении:

2. Проверочный расчет — проверяется выполнение условия прочности

3. Определение нагрузочной способности (максимального крутящего момента)

Тема 2.5. Кручение 227

Расчет на жесткость

При расчете на жесткость определяется деформация и сравни­вается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т (рис. 27.4).

При кручении деформация оце­нивается углом закручивания:

Здесь φ — угол закручивания; γ — угол сдвига; l — длина бруса; R — радиус; R = d/2. Откуда

Закон Гука имеет вид τ_к = Gγ.

Подставим выражение для γ получим

oткуда

Произведение GJ_P называют жесткостью сечения.

Модуль упругости можно определить как G = 0,4Е. Для стали G = 0,8·10⁵МПа.

Обычно рассчитывается угол закручивания, приходящийся на один метр длины бруса (вала) φ 0.

Условие жесткости при кручении можно записать в виде

где φ 0 — относительный угол закручивания, φ 0 = φ/l;

[φ 0 ] ≈ 1град/м = 0,02рад/м — допускаемый относительный угол закручивания.

228 Лекция 27

Примеры решения задач

Из расчетов на прочность и жесткость определить потреб­ный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [ φ 0] = 0,02 рад/м; модуль упругости при сдвиге G = 0,8 • 10⁵ МПа.

Решение

1. Определение размеров поперечного сечения из расчета на
прочность.

Условие прочности при кручении:

Определяем вращающий момент из формулы мощности при вра­щении:

Из условия прочности определяем момент сопротивления вала при кручении

Значения подставляем в ньютонах и мм.

Определяем диаметр вала:

2. Определение размеров поперечного сечения из расчета на
жесткость.

Условие жесткости при кручении:

Тема 2.5. Кручение 229

Из условия жесткости определяем момент инерции сечения при кручении:

Определяем диаметр вала:

3. Выбор потребного диаметра вала из расчетов на прочность и жесткость.

Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее.

Полученное значение следует округлить, используя ряд пред­почтительных чисел. Практически округляем полученное значение так, чтобы число заканчивалось на 5 или 0. Принимаем значение

dвала = 75 ММ.

Для определения диаметра вала желательно пользоваться стан­дартным рядом диаметров, приведенном в Приложении 2.

Контрольные вопросы и задания

1. Как называется напряженное состояние, возникающее при кручении круглого бруса (вала)?

2. Напишите закон Гука при сдвиге.

3. Чему равен модуль упругости материала при кручении для стали? В каких единицах он измеряется?

4. Какая связь между углом сдвига и углом закручивания?

5. Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения?

6. Напишите формулу для расчета напряжения в любой точке поперечного сечения.

7. Что такое полярный момент инерции? Какой физический
смысл имеет эта величина? В каких единицах измеряется?

Напишите формулу для расчета полярного момента инерции для круга.

230 Лекция 27

8. Напишите формулу для расчета напряжения на поверхности вала при кручении. Как изменится напряжение, если диаметр вала увеличится в два раза?

9. Почему для деталей, работающих на кручение, выбирают круглое поперечное сечение?

10. В чем заключается расчет на прочность?

11. В чем заключается расчет на жесткость?

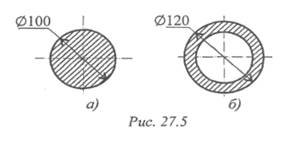
12. По величине допускаемых крутящих моментов сравнить не­сущую способность двух валов из одинакового материала, имею­щих примерно одинаковую площадь поперечных сечений с = 0,55 (рис. 27.5). Сравнение провести по формуле [М_к] = [τĸ] W_p.

13. Ответьте на вопросы тестового задания.

Тема 2.5. Кручение

Тема 2.5. Кручение 231

 

 

Поделиться:

Воспользуйтесь поиском по сайту: