Модифицированные специальные коды

Специальный код числа, в котором кроме (n+r) цифровых разрядов с весами от q^n-1 до q^-r, используется два дополнительных разряда называется модифицированным специальным кодом.

Если веса дополнительных разрядов равны qⁿ и (-qⁿ⁺¹+q^-r), то код называется модифицированным обратным и обозначается записью вида [X_q]_мок; если веса равны qⁿ и -qⁿ⁺¹, то код называется модифицированным дополнительным и обозначается записью вида [X_q]_мдк.

Дополнительный (правый) разряд модифицированного кода с весом qⁿ называется млад­шим дополнительным разрядом, а левый дополнительный разряд с весом -qⁿ⁺¹ или (-qⁿ⁺¹+q^-r) называется старшим (знаковым) дополнительным разрядом. Дополнительные разряды располагаются слева от цифровых разрядов и отделяются от них точкой.

Правило 5. При образовании модифицированного специального q-ичного кода положительного числа в оба дополнительных разряда записываются нули, а в (n+r) цифровые разряды записываются цифры прямого кода.

Таким образом, модифицированные дополнительный и обратный коды положительного числа совпадают.

Например, для числа X₁₀ = 31,425 [X₁₀]_пк = 0.31.425; [X₁₀]_мок=[X₁₀]_мдк= 00.31.425.

Правило 6. При образовании модифицированного специального кода отрицательного числа в старший (левый) дополнительный разряд записывается цифра 1, а в младший (правый) дополнительный разряд записывается цифра q-1. Значения коэффициентов x_i в цифровых разрядах модифицированного специального кода определяются по выражениям (1.26) и (1.27) соответственно.

Т.е. для получения модифицированного кода отрицательного числа осуществляют дополнение не до qⁿ, а до qⁿ⁺¹ (например, для двоичного числа осуществляют дополнение не до 2, а до 4).

Например, для числа X₈ = -157,035 имеем [X₈]_мок=17.620.742; [X₈]_мдк=17.620.743, а для числа X₂=-1001 имеем [X₂]_мок=11.0110; [X₂]_мдк=11.0111.

Модифицированный специальный код числа может явится результатом выполнения операции над числами в специальном коде. При этом, если в дополнительных разрядах комбинация цифр равна 00, то результат положительный, переполнения разрядной сетки нет; если 01, то произошло положительное переполнение разрядной сетки; если 1(q-2), то произошло отрицательное переполнение разрядной сетки; если 1 (q-1), то результат операции отрицательный, переполнения разрядной сетки нет.

Если числа представлены в естественной форме, то при переполнении разрядной сетки результат операции неверен. Знак результата определяется цифрой старшего (левого) дополнительного разряда. Анализ переполнения разрядной сетки сводится к анализу цифр в дополнительных разрядах результата.

При представлении чисел в форме с ПТ, если переполнение разрядной сетки произошло при выполнении операции над мантиссами, то осуществляется масштабное преобразование мантиссы результата. Масштабное преобразование заключается в делении мантиссы результата на основание системы счисления q (умножение на q-1), что соответствует сдвигу цифр в младшем (правом) дополнительном разряде и цифровых разрядах мантиссы на один разряд вправо. Цифра старшего (левого) дополнительного разряда при этом остается неизменной, цифра из младшего дополнительного разряда переходит в цифровой разряд с весом q-1, а на ее месте образуется цифра (q-1)q. Цифра младшего разряда при этом или теряется или запоминается. Значение порядка при этом увеличивается на единицу.

Подобное масштабное преобразование для чисел в форме с Ф3 используется иногда в процессе выполнения операций умножения и деления, цифра младшего разряда в этих случаях запоминается.

Операции сложения и вычитания чисел, представленных в модифицированных специальных кодах производятся по правилам выполнения соответствующих операций при представлении чисел в немодифицированных специальных кодах. При этом суммирование цифр в младших (правых) дополнительном разрядах выполняется в соответствии с правилами q-ичной арифметики для цифровых разрядов. Операции с цифрами в старших (левых) дополнительных разрядах и цифрой переноса из младшего (правого) дополнительного разряда выполняется в соответствии с правилами выполнения операции в дополнительных (знаковых) разрядах немодифицированных специальных кодов.

Правило 7. Преобразование модифицированного специального кода отрицательного числа в прямой код осуществляется для цифровых разрядов в соответствии с выражениями (1.26) и (1.27) для обратного и дополнительного кодов соответственно. При этом цифра старшего (левого) дополнительного разряда модифицированного кода должна быть записана в качестве кода знака прямого кода, а младший (правый) дополнительный разряд с весом qⁿ, а следовательно, и цифра в этом разряде исключается из разрядной сетки для записи прямого кода. Например, если [X₂]_мдк=11.101.01, то [X₂]_пк =1.010.11.

Пример 1.28. Выполнить операцию Z=X+Y в десятичной системе счисления при представлении операндов в модифицированных обратных кодах, если X₁₀=-25; Y₁₀=-67.

Решение. 1. Выполняем операцию в десятичной СС: Z=-25+(-67)=-92.

2. Образуем модифицированные обратные коды слагаемых и определяем модифицированный обратный код результата:

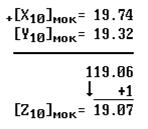
3. В соответствии с правилом 7 образуем прямой код, а затем десятичный код результата: [Z₁₀]_пк=1.92; Z₁₀=-92. Результаты выполнения операции в п.1 и 3 совпали, следовательно операция выполнена правильно. Переполнения разрядной сетки нет, так как комбинация цифр в дополнительных разрядах равна 19.

Таким образом,

1. для обозначения различной информации используют коды.

2. В современных ЦС применяются, в основном, двоичные модифицированные коды, что позволяет легко обнаружить переполнение разрядной сетки. В этом случае переполнение разрядной сетки имеет место, если комбинации цифр в дополнительных разрядах равна 01 или 10. При масштабном преобразовании цифра младшего дополнительного разряда просто повторяет (дублирует) цифру старшего дополнительного разряда.

2. Логические основы построения цифровых устройств

Основные понятия

Обработка цифровой информации в ЭВМ производится электронными схемами— цифровыми устройствами (ЦУ), которые работают с двоичными кодами.

Устройство:

Обработка сигналов в ЦУ производится в цифровой форме. Поскольку входные u_вх и выходные u_вых. сигналы часто являются аналоговыми, в состав ЦУ могут входить аналого-цифровые (АЦП) и цифроаналоговые преобразователи (ЦАП).

ЦУ

Рис.1 Структурная схема цифрового устройства

На рис. 1 представлена обобщенная структурная схема ЦУ. На вход ЦУ поступает входной аналоговый сигнал u_вх, который с помощью АЦП преобразуется в цифровой сигнал. Цифровыми сигналами представляются двоичные числа. Поэтому такие сигналы состоят из элементов только двух различных значений: 1 и 0. По установившейся терминологии эти элементы сигнала называют соответственно единицей и нулем (двоичные сигналы).

Принцип действия:

Считается, что на вход ЦУ подается множество двоичных сигналов (типичных переменных) Х=х₀, х₁,..., х_n-1, совокупность которых составляет входной алфавит ЦУ. Алфавитом называется упорядоченное множество символов, называемых буквами. Конечные последовательности букв, называются словами. Число букв в слове называют длиной слова. При изменении входного сигнала u_вх будет изменяться содержание входного алфавита ЦУ X.

В каждый дискретный момент времени t_i на вход ЦУ подается конкретная комбинация значений двоичных переменных x_i (0<i< п— 1) из входного алфавита X. В общем случае число возможных комбинаций значений двоичных переменных (слов) х, определяется по формуле:

L_x=2ⁿ (2.1)

где n—число разрядов (букв) в слове.

ЦУ осуществляет преобразование входного слова х_i и с его выхода снимается цифровой сигнал Y_k (0<k<m—1) из совокупности двоичных переменных Y=y₀y₁...y_m-1. Комбинации двоичных переменных Y образуют выходной алфавит ЦУ. Иными словами, под воздействием последовательности сигналов Х_i из входного алфавита Х на выходе ЦУ образуется последовательность выходных сигналов Y_i из алфавита Y:

Y_i=f(x_i) (2.2)

В данном выражении функция f (оператор преобразования) устанавливает соответствие между словами выходного и входного алфавитов. Такое соответствие, задаваемое с помощью конечной системы правил, принято называть алгоритмами .

Функционирование ЦУ описывается с помощью двух функций— функции переходов и функции выходов.

Функция переходов Y определяет внутреннее состояние ЦУ. Понятие состояния автомата используется для описания систем, выходные сигналы которых зависят не только от входных сигналов в данный момент времени, но и от некоторой предыстории, т. е. сигналов, которые поступили на входы ЦУ ранее. Состояние ЦУ соответствует некоторой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходные сигналы как функцию состояния и входных сигналов.

Функция выходов не что иное, как сигнал Y на выходе ЦУ.

Входные слова ЦУ представляют собой комбинации двоично-кодированных чисел фиксированной разрядности. Каждая буква х_i таких слов может принимать только два значения—0 или 1. Она называется логической двоичной переменной. Функция логических переменных, принимающая те же два значения (0 или 1), называется логической функцией (переключательной функцией)

Y^(t)=f[X^(t)] (2.3)

В дальнейшем будем оперировать понятием переключательной функции (ПФ).

Конкретная комбинация, в которой логические переменные i принимают конкретные значения, называется набором входных переменных. Число наборов входных переменных определяется по формуле (2.1). Номер набора определяется числом a, двоичный код которого принимает целочисленные значения от a=0 до a=2ⁿ-1. Набору с номером a=0 соответствует входное слово ЦА Х₀==00..00; набору a=2ⁿ-l — X₂ⁿ_-1=11...11.

12	Поделиться:

Воспользуйтесь поиском по сайту: