 |
Уравнения Максвелла в системе уравнений магнитостатики и электростатики
|
|
|
|
Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4).
В случае стационарных электрических и магнитных полей (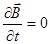
и 
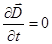) система уравнений Максвелла (1) – (4) распадается на систему
уравнений электростатики:
, 
, 
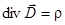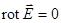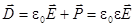(25)
и уравнений магнитостатики:
, 
, 
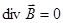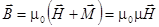, (26)
а граничные условия остаются те же.
Пример
В качестве примера решения электростатических задач можно вычислить электрическое поле, создаваемое диэлектрическим шаром радиуса R, находящемся в однородном электрическом поле 
. Уравнения электростатики в диэлектрике (25) при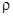 
=0 имеют вид:
, 
, 
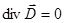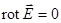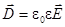(27)
Из этих уравнений следует, сто потенциал электростатического поля удовлетворяет уравнению
(28)
причём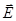 
= - 
, 
- 
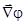. В однородном диэлектрике 
=const, поэтому уравнение (27) переходит в обычное уравнение Лапласа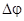 
=0.
Граничное условия (24), выражающее непрерывность вектора индукции, записывается следующим образом:
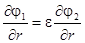при r = R (29)
Здесь 
– решение уравнения вне сферы, а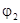 
– внутри сферы. Вместо граничного условия непрерывности тангенциальных составляющих электрического поля можно использовать эквивалентное ему условие непрерывности потенциала
|
|
|
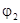= (30)
Это условие можно получить, рассматривая интеграл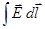 
по контуру, изображенному на рис. 2. Воспользовавшись теоремой Стокса и уравнением 
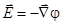, находим
Так как интеграл по любому замкнутому контуру равен нулю, то это значит, что функция 
непрерывна, откуда и следует условие (30). Из (30) очевидно так же, что
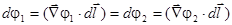
где элемент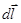 
направлен касательно к границе раздела. Из этого равенства следует, что тангенциальные компоненты вектора 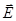также непрерывны.
Для решения поставленной задачи используем сферическую систему координат, полярная ось которой (ось z) совпадает с направлением напряжённости однородного внешнего электрического поля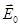 
.
Поскольку на достаточно большом удалении от диэлектрического шара электрическое поле не искажается наличием этого шара, то потенциал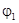 
должен удовлетворять условию
при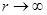 
.
Из соображений симметрии ясно, что потенциал не должен зависеть от азимутального угла, поэтому решение уравнения Лапласа запишем в виде разложения по полиномам Лежандра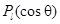 
:
,
.
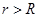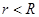Здесь потенциал нормирован так, чтобы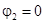 
при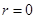 
. Так как 
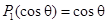, то из условия на бесконечности находим 
.
Воспользуемся теперь граничными условиями (29) и (30):
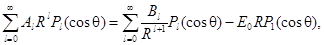
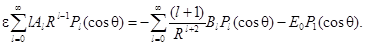
Приравнивая коэффициенты при одинаковых полиномах Лежандра, получаем
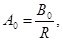
=0 при (l =0),
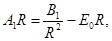
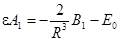при (l =1),
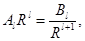
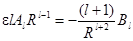при (l >1).
Из этих уравнений находим
, 
.
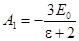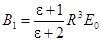Все остальные коэффициенты равны нуля, если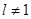 
.
Таким образом, решение задачи имеет вид:
|
|
|
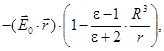(30)
Используя формулу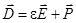 
, вычислим вектор поляризации диэлектрической сферы
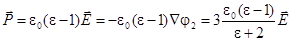
С помощью вектора поляризации формулы (30) можно записать в виде:
(31)
(32)
где 
- объём сферы.
Первые два слагаемых в (31) и (32) представляют собой потенциал однородного внешнего поля, создаваемого внешними источниками. Вторые – это потенциал электрического поля, создаваемого электрическим шаром, поляризованным внешним полем. Вне сферы – это потенциал диполя с дипольным моментом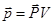 
. Внутри сферы поляризованный шар создаёт однородное электрическое поле с напряжённостью
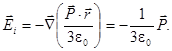(33)
Полная напряжённость внутри шара
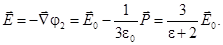(34)
Таким образом, электрическое поле внутри шара не зависят от радиуса шара и ослаблено на значение поля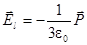 
, которое называется деполяризующим полем. Возникновение деполяризующего поля есть частный случай явления экранировки внешнего поля связанными или свободными зарядами.
Приложение.
|
|
|
