 |
Степенной ряд. Теорема Абеля. Область сходимости степенного ряда
|
|
|
|
Тема 2. Функциональные ряды. Степенные ряды
Функциональные ряды
До сих пор мы рассматривали ряды, членами которых были числа. Перейдем теперь к изучению рядов, членами которых являются функции.
Функциональным рядом называется ряд
,
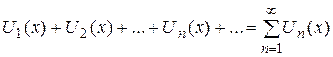членами которого являются функции одного и того же аргумента, определенные на одном множестве Е.
Например,
1. 
;
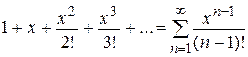2. 
;
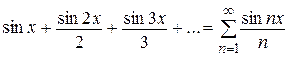3. 
.
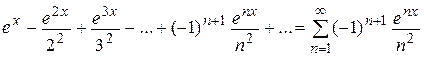Если придать аргументу х некоторое числовое значение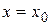 
, 
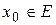, то получим числовой ряд
,
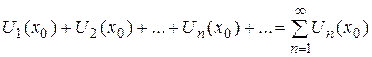который может сходиться (сходиться абсолютно) или расходиться.
Если при 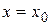полученный числовой ряд сходится, то точка 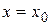называется точкой сходимости функционального ряда. Совокупность всех точек сходимости называется областью сходимости функционального ряда. Обозначим область сходимости Х, очевидно, 
.
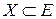Если для числовых знакоположительных рядов ставится вопрос: «Сходится ряд или расходится?», для знакопеременных – вопрос: «Сходится как – условно или абсолютно,– или расходится?», то для функционального ряда основной вопрос звучит так: «Сходится (сходится абсолютно) при каких х?».
Функциональный ряд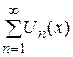 
устанавливает закон, по которому каждому значению аргумента , 
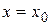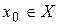, ставится в соответствие число, равное сумме числового ряда 
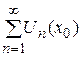. Таким образом, на множестве Х задается функция 
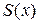, которая называется суммой функционального ряда.
Пример 16.
Найти область сходимости функционального ряда
.
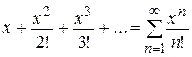Решение.
Пусть х – фиксированное число, тогда данный ряд можно рассматривать как числовой ряд, знакоположительный при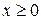 
и знакопеременный при 
.
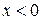Составим ряд из абсолютных величин членов данного ряда:
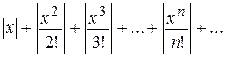
и применим к нему признак Д¢Аламбера.
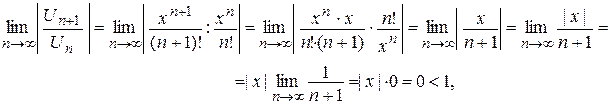
т.е для любого значения х этот предел меньше единицы, значит данный ряд сходится, причем абсолютно (так как исследовали ряд из абсолютных величин членов ряда) на всей числовой оси.
|
|
|
Таким образом, областью абсолютной сходимости является множество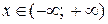 
.
Пример 17.
Найти область сходимости функционального ряда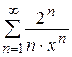 
.
Решение.
Пусть х – фиксированное число,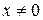 
, тогда данный ряд можно рассматривать, как числовой ряд, знакоположительный при 
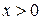и знакопеременный при .
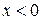Рассмотрим ряд из абсолютных величин членов данного ряда:
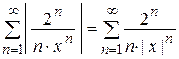
и применим к нему признак Д¢Аламбера.
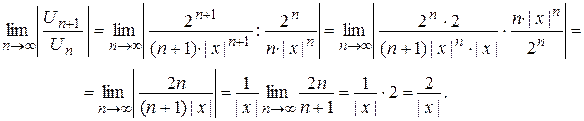
По признаку Д¢Аламбера ряд сходится, если величина предела меньше единицы, т.е. данный ряд будет сходиться, если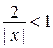 
.
Решив это неравенство, получим:
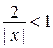Þ 
.
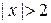Таким образом, при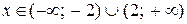 
, ряд, составленный из абсолютных величин членов данного ряда, сходится, значит, исходный ряд сходится абсолютно, а при 
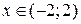данный ряд расходится.
При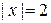 
ряд может сходится или расходится, так как при этих значениях х величина предела равна единицы. Поэтому дополнительно исследуем сходимость ряда точках 
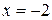и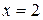 
.
Подставляя в данный ряд 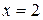, получим числовой ряд 
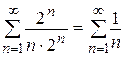, про который известно, что он является гармоническим расходящимся рядом, значит, точка 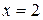– точка расходимости заданного ряда.
При 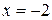получается знакочередующийся числовой ряд
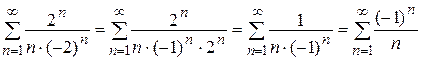
про который известно, что он сходится условно (смотри пример 15), значит, точка 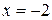– точка условной сходимости ряда.
Таким образом, область сходимости данного ряда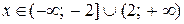 
, причем ряд сходится абсолютно при .
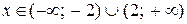Функциональный ряд
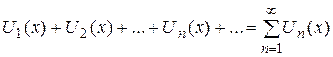
называется мажорируемым в некоторой области изменения х, если существует такой сходящийся знакоположительный ряд
,
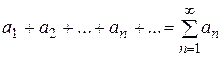что для всех х из данной области выполняется условие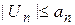 
при 
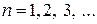. Ряд 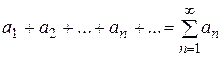называется мажорантой.
Иначе говоря, ряд является мажорируемым, если каждый его член по абсолютной величине не больше соответствующего члена некоторого сходящегося знакоположительного ряда.
Например, ряд
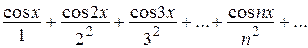
является мажорируемым для любого х, так как для всех х выполняется соотношение
|
|
|
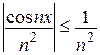при ,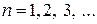
а ряд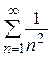 
, как известно, является сходящимся.
Теорема Вейерштрасса
Ряд, мажорируемый в некоторой области, абсолютно сходится в этой области.
Рассмотрим для примера функциональный ряд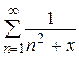 
. Этот ряд является мажорируемым при 
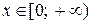, так как при 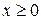члены ряда не превосходят соответствующих членов знакоположительного ряда 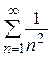. Следовательно, по теореме Вейерштрасса, рассмотренный функциональный ряд абсолютно сходится при .
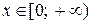Степенной ряд. Теорема Абеля. Область сходимости степенного ряда
Среди всего многообразия функциональных рядов наиболее важными с точки зрения практического применения являются степенные и тригонометрические ряды. Рассмотрим такие ряды подробнее.
Степенным рядом по степеням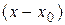 
называется функциональный ряд вида
,
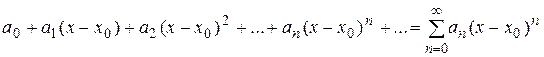где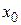 
– некоторое фиксированное число, 
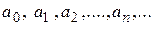– числа, называемые коэффициентами ряда.
При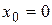 
получаем степенной ряд по степеням х, который имеет вид
.
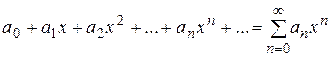Для простоты будем рассматривать степенные ряды по степеням х, так как из такого ряда легко получить ряд по степеням 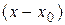, подставив вместо х выражение .
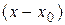Простота и важность класса степенных рядов обусловлены в первую очередь тем, что частичная сумма степенного ряда
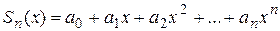
является многочленом – функцией, свойства которой хорошо изучены и значения которой легко вычисляются с помощью только арифметический операций.
Поскольку степенные ряды являются частным случаем функционального ряда, то для них так же необходимо находить область сходимости. В отличие от области сходимости произвольного функционального ряда, которая может быть множеством произвольного вида, область сходимости степенного ряда имеет вполне определенный вид. Об этом говорит следующая теорема.
Теорема Абеля.
Если степенной ряд 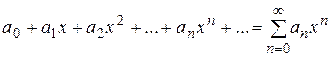сходится при некотором значении 
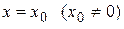, то он сходится, причем абсолютно, при всех значениях х, удовлетворяющих условию 
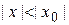. Если степенной ряд расходится при некотором значении 
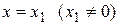, то он расходится и при значения, удовлетворяющих условию 
.
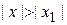Из теоремы Абеля следует, что все точки сходимости степенного ряда по степеням х расположены от начала координат недалее, чем любая из точек расходимости. Очевидно, что точки сходимости заполняют некоторый промежуток с центром в начале координат. справедлива теорема об области сходимости степенного ряда.
|
|
|
Теорема.
Для всякого степенного ряда 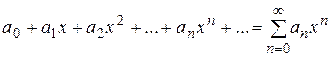существует число R (R >0) такое, что при всех х, лежащих внутри интервала 
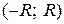, ряд сходится абсолютно и при всех х, лежащих вне интервала 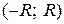, ряд расходится.
Число R называется радиусом сходимости степенного ряда, а интервал 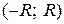– интервалом сходимости степенного ряда по степеням х.
Заметим, что в теореме ничего не говорится о сходимости ряда на концах интервала сходимости, т.е. в точках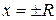 
. В этих точках различные степенные ряды ведут себя по-разному: ряд может сходиться (абсолютно или условно), а может расходиться. Поэтому сходимость ряда в этих точках следует проверять непосредственно по определению.
В частных случаях радиус сходимости ряда может быть равен нулю или бесконечности. Если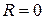 
, то степенной ряд по степеням х сходится лишь в одной точке 
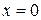; если же 
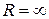, то степенной ряд сходится на всей числовой оси.
Еще раз обратим внимание на то, что степенной ряд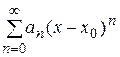 
по степеням 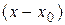может быть сведен к степенному ряду 
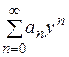с помощью замены 
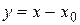. Если ряд 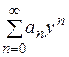сходится при 
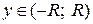, т.е. для 
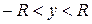, то после обратной замены получим
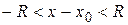Þ 
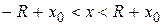или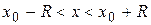 
.
Таким образом, интервал сходимости степенного ряда 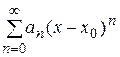имеет вид 
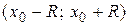. Точку 
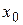называют центром сходимости. Для наглядности принято интервал сходимости изображать на числовой оси (рисунок 1)
 |
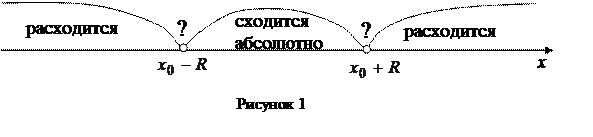Таким образом, область сходимости состоит из интервала сходимости, к которому могут быть добавлены точки 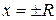, если в этих точках ряд сходится. Интервал сходимости можно находить, применяя непосредственно признак Д¢Аламбера или радикальный признак Коши к ряду, составленному из абсолютных величин членов данного ряда.
Пример 18.
Найти область сходимости ряда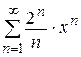 
.
Решение.
Данный ряд является степенным рядом по степеням х, т.е. 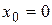. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда, и воспользуемся признаком Д¢Аламбера.
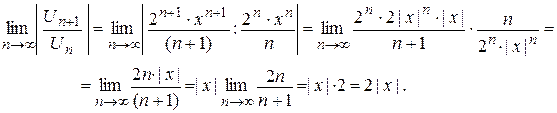
Ряд будет сходиться, если величина предела меньше 1, т.е.
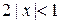, откуда 
.
|
|
|
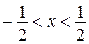Таким образом, интервал сходимости данного ряда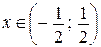 
, радиус сходимости 
.
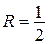Исследуем сходимость ряда на концах интервала, в точках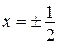 
. Подставляя в данный ряд значение 
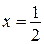, получим ряд
.
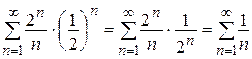Полученный ряд является гармоническим расходящимся рядом, следовательно, в точке 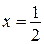ряд расходится, значит, точка 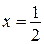не входит в область сходимости.
При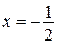 
получим знакочередующийся ряд
,
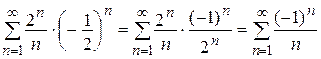который является условно сходящимся (пример 15), следовательно, точка 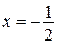–точка сходимости (условной).
Таким образом, область сходимости ряда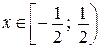 
, причем в точке 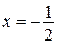ряд сходится условно, а в остальных точках — абсолютно.
Рассуждениям, использованным при решении примера, можно придать общий характер.
Рассмотрим степенной ряд
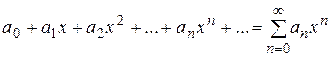
Составим ряд из абсолютных величин членов ряда и применим к нему признак Д'Аламбера.
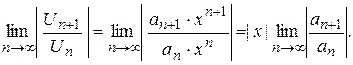
Если существует (конечный или бесконечный) предел, то по условию сходимости признака Д'Аламбера ряд будет сходиться, если
,
,
.
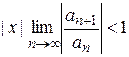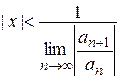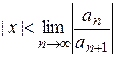Отсюда из определения интервала и радиуса сходимости имеем
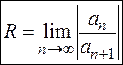
Применяя радикальный признак Коши и рассуждая аналогично, можно получить еще одну формулу для нахождения радиуса сходимости
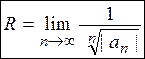
Пример 19
Найти область сходимости ряда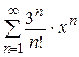 
Решение.
Ряд является степенным по степеням х. Для нахождения интервала сходимости вычислим радиус сходимости по приведенной выше формуле. Для данного ряда формула числового коэффициента имеет вид
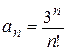, тогда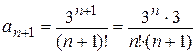 
Следовательно,
.
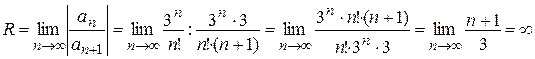Так как R = ¥, то ряд сходится (причем абсолютно) при всех значения х, т.е. область сходимости х Î (–¥; +¥).
Заметим, что можно было бы найти область сходимости без использования формул, а применяя непосредственно признак Д' Аламбера:
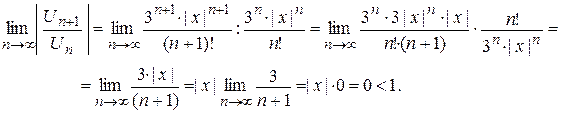
Так как величина предела не зависит от х и меньше 1, то, значит, ряд сходится при всех значениях х, т.е. при х Î(-¥;+¥).
Пример 20
Найти область сходимости ряда
1!(х +5)+2!(х + 5)2 +3!(х + 5)3 +... + п!(х + 5) п +...
Решение.
Данный ряд является степенным рядом по степеням (х + 5),т.е. центр сходимости х 0 = -5. Числовой коэффициент ряда ап = п!.
Найдем радиус сходимости ряда
.
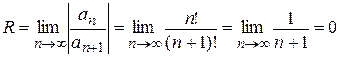Таким образом, интервал сходимости состоит из одной точки – центра интервала сходимости х = -5.
Пример 21
Найти область сходимости ряда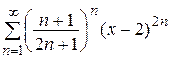 
.
Решение.
Данный ряд является степенным рядом по степеням (х –2),т.е.
центр сходимости х 0 = 2.Заметим, что ряд является знакоположительным при любом фиксированном х, так как выражение (х- 2)возводится в степень 2 п. Применим к ряду радикальный признак Коши.
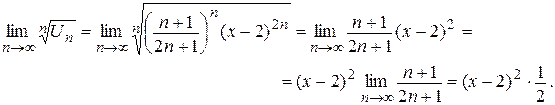
Ряд будет сходиться, если величина предела меньше 1, т.е.
, 
, 
,
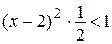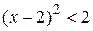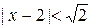значит, радиус сходимости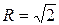 
, тогда интеграл сходимости
, 
.
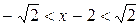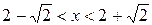Таким образом, ряд сходится абсолютно при х Î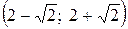 
. Обратим внимание, что интеграл сходимости симметричен относительно центра сходимости х о = 2.
|
|
|
Исследуем сходимость ряда на концах интервала сходимости.
Полагая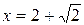 
, получим числовой знакоположительный ряд
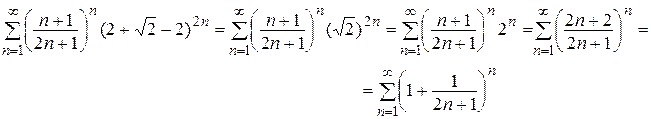Воспользуемся необходимым признаком сходимости:
,
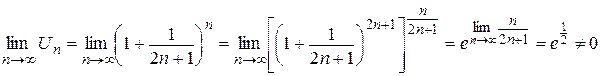следовательно, числовой ряд расходится, и точка 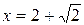является точкой расходимости. Заметим, что при вычислении предела использовали второй замечательный предел.
Полагая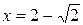 
, получим тот же числовой ряд (проверить самостоятельно!), значит, точка 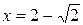также не входит в интервал сходимости.
Итак, область абсолютной сходимости данного ряда х Î .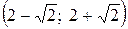
|
|
|
