 |
Глава 2. Моделирование экономических процессов
|
|
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
НОУ "Московский институт управления"
Кафедра: Экономики и управления
Специальность: Экономика и управление на предприятии (в природопользовании)
Форма обучения: заочная
РАБОТА ПО ПРОЙДЕННОМУ КУРСУ
По дисциплине: " АНАЛИЗ И ДИАГНОСТИКА ФИНАНСОВО-ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ "
Тема: "Математическое моделирование производственной деятельности"
студента учебной группы
Мельников Дмитрий Александрович
Руководитель:
МОСКВА 2010 г.
Содержание
Введение
Глава 1. Что такое математическое моделирование?
1.1 Основные этапы математического моделирования
1.2 Классификация моделей
Глава 2. Моделирование экономических процессов
2.1 Моделирование экономических процессов
2.2 Этапы исследования экономических процессов
2.3 Системные предпосылки формирования модели системы управления маркетинговой деятельностью предприятия сферы услуг
Заключение
Используемая литература
Введение
Важными задачами совершенствования производственно-экономических систем (ПЭС) являются повышение эффективности функционирования экономических объектов и достижение высоких конечных результатов деятельности на основе рационального использования производственных ресурсов.
В этом аспекте актуальными являются проблемы оценки эффективности использования ресурсов и функционирования экономических систем различных уровней и масштабов: от отраслевых производственно-хозяйственных комплексов федерального и регионального уровня, до первичных звеньев экономики - промышленных объединений и предприятий.
Решение этих проблем должно опираться на комплексный анализ функционирования производственно-экономических систем, идентификацию характеристик протекающих процессов. Результаты решения таких задач востребованы практикой совершенствования процессов управления производственно-хозяйственной деятельностью объектов экономических отношений в условиях становления современных рыночных механизмов. В концептуальном плане решение таких проблем формирует необходимую информацию для принятия и поддержки эффективных управленческих решений.
|
|
|
В целом, построение экономико-математических моделей и математическое моделирование на их основе являются современным научным направлением, позволяющим вскрывать сущность протекающих экономических процессов, эффективно управлять их поведением и анализировать функционирование экономических объектов и систем.
Глава 1. Что такое математическое моделирование?
С середины XX в. в самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, как "математическая экономика", "математическая химия", "математическая лингвистика" и т.д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.
Математическая модель - это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования - исследовать эти объекты и предсказать результаты будущих наблюдений. Однако моделирование - это еще и метод познания окружающего мира, дающий возможность управлять им.
Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории, чтобы проверить, "что было бы, если бы..." Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.
|
|
|
Основные этапы математического моделирования
1) Построение модели. На этом этапе задается некоторый "нематематический" объект - явление природы, конструкция, экономический план, производственный процесс и т.д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.
2) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.
3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.
4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.
5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.
Классификация моделей
Классифицировать модели можно по разным критериям. Например, по характеру решаемых проблем модели могут быть разделены на функциональные и структурные. В первом случае все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие - как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа (дифференциальных, алгебраических и т.д.), устанавливающих количественные зависимости между рассматриваемыми величинами. Во втором случае модель характеризует структуру сложного объекта, состоящего из отдельных частей, между которыми существуют определенные связи. Как правило, эти связи не поддаются количественному измерению. Для построения таких моделей удобно использовать теорию графов. Граф - это математический объект, представляющий собой некоторое множество точек (вершин) на плоскости или в пространстве, некоторые из которых соединены линиями (ребрами).
|
|
|
По характеру исходных данных и результатов предсказания модели могут быть разделены на детерминистические и вероятностно-статистические. Модели первого типа дают определенные, однозначные предсказания. Модели второго типа основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер.
Глава 2. Моделирование экономических процессов
В настоящее время одним из наиболее популярных методов исследования бизнес-процессов является имитационное моделирование.
На основе имитационной модели можно построить самые точные и действенные методы анализа и прогнозирования показателей эффективности бизнес-процессов. Тем не менее, нужно быть осторожным и не использовать некорректные процедуры анализа и моделирования, которые могут привести к неточным результатам. В основе имитационной модели лежат понятия потоков, уровней и темпов.
При построении имитационной модели обычно вводят в рассмотрение три потока [96]:
информационный;
финансовый;
кадровый.
Процедуры построения финансовой, кадровой и информационной маркетинговых систем существенным образом зависят от специфики конкретного предприятия и в обобщенном виде могут быть представлены в виде системы дифференциальных уравнений, связывающих основные уровни и темпы (скорости изменения уровней системы):
где:
вектор уровней системы, построение которого, по словам К. Шеннона [103], является скорее искусством;
|
|
|
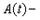матрица темпов.
известная вектор-функция внешних детерминированных воздействия, например инвестиций.
случайные воздействия на систему. Обычно предполагается, что случайный Марковский процесс (белый шум) с известными вероятностными характеристиками.
Цель моделирования экономических процессов, как правило, состоит в получении устойчивой схемы, поскольку последовательность оказываемых услуг повторяется. Важной процедурной концепцией анализа эффективности и обеспечения качества управления является определение периода неустойчивой работы и устранение искажения, вносимого статистическими данными, собранными за такой период. При реализации имитационной модели на компьютере дифференциальные уравнения заменяются конечно-разностными, и, именно такие уравнения используются в различных имитационных моделях.
где:
- шаг моделирования;
- матрица темпов увеличения, с индексом “-” матрица темпов уменьшения;
- внешние воздействия;
- случайные возмущения.
|
|
|
