 |
Приложение. Математическая модель: веревка и нагрузки, возникающие в ней при срыве
|
|
|
|
Приведем вывод формулы, описывающей поведение альпинистской веревки при срыве первого в связке.
П=P·(H+L+ΔL) — потенциальная энергия человека
P — вес человека (P=mg)
H — превышение человека над последней точкой страховки
L — длина свободной веревки
ΔL — длина, на которую веревка максимально растянулась
Аторм=Fторм·Δs — работа сил трения в тормозном устройстве
Fторм — сила трения веревки в тормозном устройстве
Δs — длина протравливания веревки
Учтем силы трения в карабине:
F1=F-Fтрен
Fтрен=f·N=f·(F+F1)=f·(2F-Fтрен)
Fтрен=(2f/(1+f))·F, где f — коэффициэнт трения
N=2F-Fтрен=(2f/(1+f))·F
Атрен=(1/2)·Fтрен·ΔL' — работа сил трения в карабине (сила трения меняется линейно, одновременно с силой F, от нуля до максимального значения Fтрен, поэтому в формуле присутствует коэффициент 1/2).
ΔL=ΔL'+ΔL'' — растяжение веревки складывается из растяжения веревки со стороны базы ΔL' и растяжения веревки со стороны сорвавшегося ΔL''.
E=(1/2)·(F·ΔL''+F1·ΔL') — энергия деформации веревки.
E+Атрен=(1/2)·(F·ΔL''+F1·ΔL')+(1/2)·Fтрен·ΔL'
E+Атрен=(1/2)·(F·ΔL''+(F-Fтрен)·ΔL'+Fтрен·ΔL')=(1/2)F·ΔL
F=α·(ΔL/Lo) — сила рывка (усилие деформации веревки)
α — коэффициент упругости веревки
Lo — общая длина ненагруженной веревки
ΔL=ΔL'+ΔL''=(1/α)·(F·L+F1·L1)=(1/α)·(F·L+(F-Fтрен)·L1)
ΔL=(1/α)·(F·L+(F·(1-(2f/(1+f))·L1=(1/α)·(F·L+F·L1-(2f/(1+f))·F·L1)
ΔL=(F·Lo/α)·(1-(2f/(1+f))·(L1/Lo))
L1 — длина веревки между базой и верхней (последней) точкой
K=(H+L)/Lo — фактор рывка
П=Е+Атрен+Аторм — из закона сохранения энергии следует, что потенциальная энергия человека П переходит в энергию деформации веревки Е, и работу сил трения в карабине Атрен и работу сил трения в тормозном устройстве Аторм.
После подстановки предыдущих выражений в закон сохранения энергии получим:
P·(H+L+ΔL)=(1/2)F·ΔL+Fторм·Δs
(1/2)F·ΔL-P·ΔL-P(H+L-(Fторм/P)·Δs)=0, разделим выражение на Lo
(1/2)F·(ΔL/Lo)-P·(ΔL/Lo)-P((H+L)/Lo-(Fторм/P)·(ΔL/Lo))=0
(1/2)F·(ΔL/Lo)-P·(ΔL/Lo)-P(K-(Fторм/P)·(ΔL/Lo))=0 (K —фактор рывка)
|
|
|
Подставим сюда полученное выражение для ΔL=(F·Lo/α)·(1-(2f/(1+f))·(L1/Lo))
=0
Получаем следующее решение уравнения для F:
— сила рывка веревки.
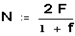— рывок на карабин.
— рывок на базу (или страхующего).
— относительное удлинение веревки при величине рывка на веревку F.
Теперь рассчитаем время воздействия рывка на сорвавшегося и распределение этого рывка во времени. После срыва человек падает вниз и веревка начинает нагружаться, тормозя падение человека и действуя как амортизатор. На человека со стороны веревки действует силы:
F=-(α/Lo)·ΔL — сила упругости веревки;
P=mg — сила тяжести (Р — вес человека).
Будем считать, что затухания нет. В этом случае уравнение движения запишется следующим образом:
m·ΔL''+(α/Lo)·L=mg
ΔL''+(α/(mLo))·ΔL=g
решением данного дифференциального уравнения есть функция:
это косинусоида, смещенная на величину ((mg)/α)·Lo (гармонические колебания).
Для величины силы упругости (рывка веревки) мы имеем следующую зависимость силы от времени: F(t)=m·ΔL''
— как видно — это тоже косинусоида.
— полупериод колебаний при рывке.
| Fmax=-(α/Lo)·ΔLmax | 
|
|
| T/2 (время) |
Рывок можно охарактеризовать временем воздействия на человека и элементы страховки — полупериодом косинусоиды. За это время сила рывка возрастает от нуля до максимума и снова уменьшается до нуля.
Надо еще заметить, что данное уравнение описывает поведение системы лишь при натянутой веревке. При движении в верхней части (положительный период косинусоиды) сила упругости на человека не действует, и движение происходит только за счет силы тяжести (L''=g, это движение по параболе), но это не особо интересно для рассмотрения процесса страховки. После первого полупериода за счет диссипативных сил происходит уменьшение амплитуды колебаний (период не меняется). Если элементы страховочной цепи выдержали первый рывок, последующие не окажут существенного воздействия.
|
|
|
Время воздействия рывка нам интересно для оценки его жесткости: жесткость рывка тем выше, чем больше его сила и чем меньше время его воздействия. Короткий рывок оказывает более разрушающее воздействие, чем более плавный рывок, имеющий такую же силу.
Библиография
1. Technique de1’alpinisme, sous der de Bernard Amy. France, 1977. (Ветер странствий № 16, ФИС, 1981 г.).
2. Герман Хубер. Альпинизм сегодня. М., ФИС, 1980 г.
3. Ф. Кропф. Спасательные работы в горах. М., 1975 г.
4. Е. Казакова
5. Ветер странствий № 18, ФИС, 1983 г.
6. Mountaineering. The freedom of the hills. 5-th edition. 1991.
7. Веб-сайт компании Petzl (www.petzl.com).
8. Веб-сайт компании Beal (beal-planet.com).
|
|
|
