 |
Вопрос 1. Показатели вариации в статистике
|
|
|
|
Содержание
1. Теоретическая часть...................................................................................3
1.1. Вопрос 1. Показатели вариации в статистике..........................................3
1.2. Вопрос 2. Средние и индексы структурных сдвигов.............................7
1.3. Библиографический список......................................................................9
2.Практическая часть....................................................................................10
Теоретическая часть
Вопрос 1. Показатели вариации в статистике
Вариация – ϶ᴛᴏ различия индивидуальных значений признака у единиц изучаемой совокупности.
Применение. Исследование вариации имеет большое практическое значение и будет необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, реализует ϲʙᴏю основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию. В наибольшей степени вариации подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды времени и в разных местах.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают:
· размах вариации 
· среднее линейное отклонение 
· дисперсию 
· среднее квадратическое отклонение 
Относительные показатели вариации включают:
|
|
|
· Коэффициент осцилляции 
· Относительное линейное отклонение (линейный коэффициент варианции) 
· Коэффициент вариации (относительное отклонение) 
Основными показателями, характеризующими вариацию, являются:
· Размах вариации (R)
Размах вариации – ϶ᴛᴏ разность между максимальным и минимальным значениями признака. Он показывает пределы, в кᴏᴛᴏᴩых изменяется величина признака в изучаемой совокупности.
R = Xmax – Xmin
Пример:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
Решение: R = 9 - 2 = 7 лет.
Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.
· Дисперсия ( ) лишена этого недостатка. Она рассчитывается как средний квадрат отклонений значений признака от их средней величины:
|
·
|
Упрощенный способ расчета дисперсии осуществляется с помощью следующих формул (простой и взвешенной):
|
·
|
· Широко распространенным на практике показателем является среднее квадратическое отклонение ():
|
Среднее квадратическое отклонение определяется как квадратный корень из дисперсии и имеет ту же размеренность. Среднее квадратическое отклонение, кᴏᴛᴏᴩое называют стандартом (или стандартным отклонение).
Пример:
Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них,
· коэффициент вариации измеряет колеблемость в относительном выражении – относительно среднего уровня, что во многих случаях является предпочтительнее.
|
· Среднее линейное отклонение ( )
Среднее линейное отклонение – ϶ᴛᴏ средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
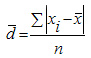
Пример:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
|
|
|
Решение: 
лет;
Ответ: 2,4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
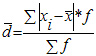
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
|
|
|
